 |
Пример решения типовой задачи
|
|
|
|
ТЕОРИЯ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Методические указания к практическим занятиям
ВВЕДЕНИЕ
Термин «принятие решений» встречается в различных научных дисциплинах. Прежде всего, следует назвать экономику, где исследуются проблемы разумного, рационального использования ограниченных ресурсов потребителем и производителем.
Исследование операций – это наука, изучающая принятие решений и их технологию. Научная составляющая связана с проблемами моделирования решений путем определения целей лица, принимающего решение (ЛПР), и условий, в которых ЛПР должны или желают работать. Научная составляющая также связана с математическими методами для оптимизации моделей решения. Технологическая составляющая связана с инструментами программного обеспечения для сбора и обработки данных, использования их при создании и оптимизации моделей, а также для составления отчетов о результатах.
Цель практических занятий – познакомить студентов с теорией принятия решений, дать навыки решения задач принятия решений (ЗПР).
На практических занятиях студенты знакомятся со следующими математическими методами исследования операций:
- инструменты теории полезности;
- линейное программирование;
- критерии принятия решений в условиях риска и неопределенности;
- инструменты теории игр;
- инструменты финансовой математики.
В качестве программного обеспечения для решения ЗПР на практических занятиях используется приложение Microsoft Office Excel.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Все задачи принятия решений подразделяются на следующие группы:
- детерминированные ЗПР;
- ЗПР в условиях риска;
- ЗПР в условиях неопределенности;
|
|
|
- ЗПР в условиях конфликта.
1.1. Решение детерминированных задач приятия решений
Для детерминированных ЗПР известна ситуация, в условиях которой реализуется решение. Наиболее известным и широко используемым инструментом теории принятия решений для решения данных задач выступает линейное программирование, как математический метод решения задач оптимального распределения имеющихся ресурсов для достижения определенной цели (наибольшего дохода или наименьших затрат). На занятиях рассматриваются следующие основные типы задач линейного программирования:
- задачи о составлении смеси, цель которых заключается в выборе наиболее экономичной смеси ингредиентов при учете ограничений на физический или химический состав смеси и на наличие необходимых составляющих;
- задачи производства, целью которых является подбор наиболее выгодной производственной программы выпуска продукции при использовании ограниченных источников сырья;
- задачи распределения (транспортные задачи), цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время, затраченное на нее, либо комбинация того и другого.
При решении детерминированных ЗПР на занятиях используется табличный оптимизатор «Поиск решения» приложения Excel.
1.2. Решение задач принятия решений в условиях риска
Для задач принятия решений в условиях риска характерно наличие множества ситуаций, в которых будет реализовываться каждое решение, а также известны вероятности наступления этих ситуаций.
В данной теме изучаются основы теории полезности, аксиомы рационального выбора, функция полезности и дерево решений, как инструмент для нахождения последовательности правильных решений, ведущих к максимальной ожидаемой полезности.
|
|
|
Кроме этого рассматриваются следующие критерии принятия решений:
- модальный критерий;
- критерий Байеса;
- критерий максимизации вероятности распределения оценочного функционала.
1.3. Решение задач принятия решений в условиях неопределенности
Для задач принятия решений в условиях неопределенности информация о вероятностях наступления определенных состояний среды либо неизвестна, либо точно не определена.
Выбор решения в данном случае осуществляется в соответствии с определенным критерием принятия решения. Студентам предлагаются на изучение следующие критерии:
- критерий Лапласа;
- критерий Вальда (критерий крайнего пессимизма);
- критерий Сэвиджа (критерий минимальных рисков);
- критерий Гурвица.
1.4. Решение задач принятия решений в условиях конфликта
В конфликте участвуют две или более сторон, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Реальный конфликт очень сложен, поэтому для его анализа строят модель конфликта, которую принято называть игрой. Теория игр – это раздел математики, изучающий игры.
В данном вопросе студентам излагаются основы теории игр, касающиеся антагонистических парных игр и биматричных игр, даются методы решения игр порядка 2х2, nx2, 2xm, nxm.
1.5. Решение задач принятия финансовых решений
В данной теме студентам даются основы финансовой математики, а именно вводятся понятия простого и сложного процента, дисконтирования и приращения, изучаются вопросы приведения денежных потоков к сопоставимому по времени виду, даются методы оценки инвестиционных проектов.
ПРИМЕР РЕШЕНИЯ ТИПОВОЙ ЗАДАЧИ
Решим транспортную задачу (ТЗ). Цель задачи – минимизация полной стоимости распределения (транспортировки) товаров со складов потребителям.
2.1. Теоретическая часть
Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукцииодного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.
Входные параметры модели ТЗ:
|
|
|
- n – количество пунктов отправления;
- m – количество пунктов назначения;
- 
– запас продукции в пункте отправления 
(
) [ед. тов.];
- 
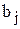– спрос на продукцию в пункте назначения 
(
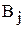) [ед. тов.].
- 
– транспортный тариф или стоимость перевозки единицы продукции из пункта отправления в пункт назначения 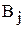[руб./ед. тов.].
Выходные параметры модели ТЗ:
- 
– количество продукции, перевозимой из пункта отправления в пункт назначения 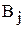[ед. тов.];
- СS – транспортные расходы на перевозку всей продукции [руб.].
Этапы построения модели транспортной задачи:
- определение переменных;
- проверка сбалансированности задачи;
- построение сбалансированной транспортной матрицы;
- задание целевой функции;
- задание ограничений.
Модель транспортной задачи задается в следующем виде:
 ;
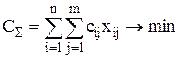| (1) |
Целевая функция представляет собой транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица (табл. 1).
Таблица 1
|
|
|
