 |
Передаточная функция турбины.. Уравнение синхронной машины.
|
|
|
|
Передаточная функция турбины.
Определяется адекватностью модели турбины.
1) линеаризованная модель пропускания пара.
2) модель с учетом паровых объемов.
В простейшем случае
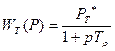
- постоянная времени парового объема турбины.
Даннаяа постоянная времени определяется характером регулирования турбины (наличие дросселирования, сопловое регулирование турбины, а также наличие промежуточного пароперегревателя и числа цилиндров, участвующих в регулировании).
В простейшем случае
, где 
о. е.
При наличии промежуточного пароперегревателя появляются дополнительные передаточные функции пароперегревателя и ЦСД и ЦВД. Соответственно в этом случае порядок дифференциальных уравнений для турбины будет равен 3.
СМ: сервомотор
Уравнение синхронной машины.
Особенности записи уравнений синхронной машины заключается в том, что не учитываются поля высших гармонических составляющих, в частности, берутся только 2 первых члена из ряда Тейлора для получения эквивалентной индуктивности машины.
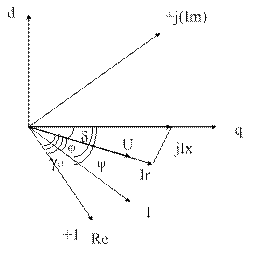
Кроме того, не учитывается частотная зависимость сопротивлений синхронной машины, запись уравнений синхронной машины будет выполняться в осях q, d и 0.
{ 
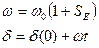
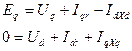
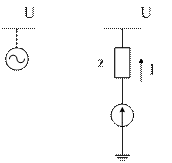
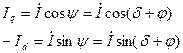
Введем угол 
Далее необходимо записать проекции:
- периодическая функция, где 
, ( 
- частота сети)
А – произвольный параметр,
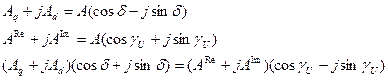
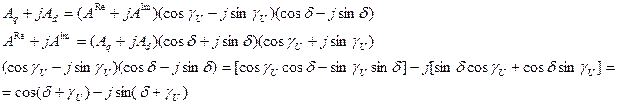
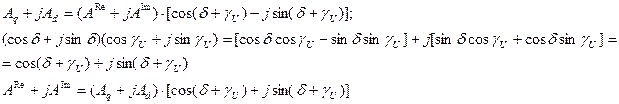
Для перехода к выражениям потокосцепления.
Допущение:
Пусть в начальный момент времени угол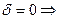 
из формулы угол 
будет исключен, разницы между 
и не будет, будут совпадать.
При условии:
1. 
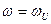, т. е.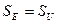 
2. 
Уравнения обратного преобразования координат:
{ 
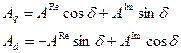
Уравнения прямого преобразования координат:
|
|
|
{ 
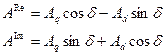
Дифференциальные уравнения обмоток ротора.
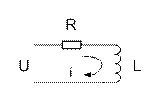
- закон Ома в дифференциальной форме без учета емкостной составляющей.
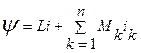
Потокосцепление обмотки возбуждения:
Обмотка возбуждения закладывается по продольной оси.
Для l-го демпферного контура:
Выражение по оси q:
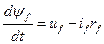
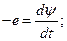
Поскольку выводы из статорных цепей коммутируют на шины, связанные с сетью, уравнение статорных цепей получаем из уравнений, записанных в синхронных осях Re, Im (j, +1).
- общее выражение для статорных цепей
Запишем уравнение в проекциях
Выполним преобразование данной системы с помощью уравнений прямого преобразования координат.
Для упрощения формы записи примем, что 
.
Тогда проекция параметра А на вещественную ось:
{ 
{ 
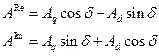где 
- периодическая функция.
Возьмем производную для данной схемы.
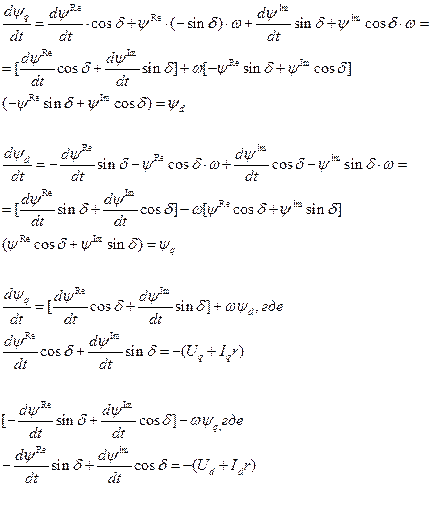
Нужно сделать подстановку
Окончательно:
Необходимо отметить, что полученная система дифференциальных уравнений определяет общую форму записи уравнений переходных процессов синхронной машины.
Данная форма может быть приведена к форме записи токов после введения дополнительных преобразований.
Полученные уравнения необходимо использовать в совокупности с линейными алгебраическими уравнениями потокосцеплений в матричной форме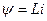 
. При этом токи должны рассчитываться исходя из уравнений баланса электрической сети в нормальном или установившимся режиме работы.
При анализе режимов, отвечающих процессам регулирования частоты и активной мощности в ЭЭС нет необходимости пользоваться полученными уравнениями идеализированной синхронной машины. Это связано с тем, что нет необходимости учитывать электромагнитные переходные процессы.
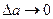(отключение параметров работы ЭЭС к 0)
Все производные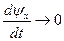 
.
|
|
|
(не учитываются насыщение и высшие гармоники)
Достаточно воспользоваться уравнением позиционной модели синхронной машины.
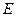за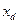 
будет отвечать адекватному моделированию при следующих допущениях:
а)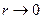 
. Пренебрегаем резистивными потерями.
б)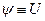 
Данные допущения будут вносить искажения характера протекания переходного процесса в его начальной стадии (т. е. в момент возмущения).
Наброс нагрузки.
Искажения → потокосцепления будут претерпевать скачок в момент возмущения. В реальности это не так.
Также претерпевать скачок в момент возмущения будет электрический угол или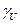 
.
Уравнения движения останутся теми же самыми.
|
|
|
