Средние и среднеквадритичные нагрузки

Важное значение в расчетах и при исследовании нагрузок, а так же при подсчетах расхода и потерь Эл.энергии имеют средняя мощность за наиболее загруженную смену Рсм, Qсм и среднегодовая мощность Рсг, Qсг. Величины Рсм, Qсм находятся по показателям, которые определяют путем простейших обследований нагрузок и проверяют по удельным расходам производств.

Средняя активная мощность за наиболее загруженную смену какой-либо группы силовых приемников с одинаковым режимом работы определяется путем умножения суммарной номинальной мощности группы рабочих приемников Рном, приведенной для приемников повторно-кратковременного режима (ПКР) работы к ПВ=100%, на их групповой коэф. Использования Рсм=kиа*Pном

Среднюю реактивную мощность за наиболее загруженную смену Qсм для какой либо группы силовых приемников(с отстающим током) одинакового режима работы определяют:

1.Умножением суммарной номинальной реактивной мощности группы рабочих приемников Qном, приведенной для приемников ПКР и ПВ=100% на их групповой коэффициент использования Qсм=kиp*Qном

2.Умножением средней активной мощности Рсм этой группы на tgφ, соответствующий групповому коэф-ту мощности Qсм=Рсм* tgφ

Реактивные нагрузки приемников с опережающим током принимают со знаком «-».

Среднегодовую мощность, потребляемую цехом или предприятием в целом, находим из соотношений Рсг=Эаг/Тг; Qсг= Эрг/Тг, где Тг – годовой фонд рабочего времени, определяемый при проектировании по данным технологического процесса производства.

Среднегодовая мощность может быть так же определена из выражений

Рсг=Киаг*Рном; Qсг=Кирг*Qном

Условные средние нагрузки за наиболее загруженную смену трехфазной сети от группы однофазных приемников одинакового режима работы (при числе приемников более3-х), включенных на фазное или линейное напряжение сети, определяется по формулам:

Рсм.у=3Ки*Рн.м.ф.; Qсм.у=3Кир*Qн.м.ф.

При наличии в узле системы Эл.снабжения приемников однофазного и трехфазного тока средние нагрузки узла за наиболее загруженную смену определяются суммированием средних нагрузок трехфазных приемников и условных средних нагрузок трехфазной сети от однофазных приемников.

При ориентировочных расчетах, когда отсутствуют данные для определения Рсм и Qсм эти величины могут быть определены из выражений

Рсм=Рсг/Ксэ; Qсм=Qсг/Ксэр

Ксэ;Ксэр – годовой коэф. Сменности по энергопользованию активной и реактивной энергии.

Рсг;Qсг – среднегодовые активные и реактивная мощности.

Определение среднеквадратичной мощности в условиях эксплуатации может быть произведено по показаниям счетчиков Эл.энергии согласно выражениям Рсм=Кф*Рс Qсм=Кфр*Qc, где величины Кф и Кфр определяются опытным путем.

По среднеквадратичной мощности подсчитывается среднеквадратичный ток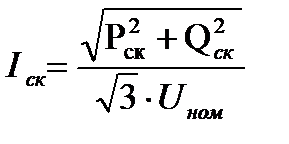

13. Ос­нов­ные по­ложения тео­рии ве­ро­ят­но­стей в рас­че­тах элек­три­че­ских на­гру­зок.

Обыч­но при про­ек­ти­ро­ва­нии име­ют де­ло с груп­по­вы­ми гра­фи­ка­ми на­гру­зок, ко­то­рые в аб­со­лют­ном боль­шин­ст­ве но­сят ве­ро­ят­но­ст­ный ха­рак­тер. Они пе­ре­мен­ны в те­че­нии от­дель­ных ра­бо­чих цик­лов, по­это­му в тео­рии рас­че­тов элек­три­че­ских на­гру­зок при­ме­ня­ет­ся тео­рия ве­ро­ят­но­сти и ста­ти­сти­ки.

Т_б – ба­зис­ное вре­мя.

Ка­ж­дая сту­пень гра­фи­ка на­груз­ки пред­став­ля­ет со­бой слу­чай­ное со­бы­тие. Ве­ро­ят­ность слу­чай­но­го со­бы­тия оп­ре­де-ля­ет­ся час­то­той по­яв­ле­ния это­го со­бы­тия.

Е[P=P_n]=Δt_n/T_б – ве­ро­ят­ность по­яв­ле­ния Р_n

Ес­ли по оси абс­цисс от­кла­ды­вать вре­мя в от­но­си­тель­ных еди­ни­цах, т.е. T_б=1, то

гра­фик при­мет сле­дую­щий вид:

В этом слу­чае лю­бая ве­ро­ят­ность Р_n на­груз­ки бу­дет оп­ре­де­лять­ся дли­ной от­рез­ка вре­ме­ни Δt_n.

Учи­ты­вая, что ве­ро­ят­ность двух слу­чай­ных не­со­вмес­ти­мых со­бы­тий в Σ-ме рав­на 1, то Е[P>P_n]=1-Е[P<P_n];

Ес­ли по­вер­нуть гра­фик по на­прав­ле­нию w на 90^о, то по­лу­чим кри­вую (за­кон рас­пре­де­ле­ния) ψ[Р] слу­чай­ной на­груз­ки Р от ве­ро­ят­но­сти по­яв­ле­ния.

ψ[Р]=Е[P<P_n]

За­кон рас­пре­де­ле­ния слу­чай­ной на­груз­ки оп­ре­де­ля­ет­ся сле­дую­щи­ми ха­рак­те­ри­сти­ка­ми:

- мат. ожи­да­ние на­груз­ки;

- дис­пер­си­ей на­груз­ки;

- сред­не­квад­ра­тич­ным от­кло­не­ни­ем на­груз­ки или стан­дар­том на­груз­ки.

М[Р]=Р_с – ма­те­ма­ти­че­ское ожи­да­ние на­груз­ки (сред­няя на­груз­ка Р_с)

M[ΣP_i]=ΣM[P_i]=ΣP_ci=P_c

Дис­пер­сия на­груз­ки – это ма­те­ма­ти­че­ское ожи­да­ние квад­ра­та цен­три­ро­ван­ной слу­чай­ной на­груз­ки.

Д[P]=M[(P-P_c)²]=M[(P²-2PP_c+P_c²)]=M[P²]-M[2PP_c]+M[P_c²];

M[P]=P_c;

M[P²]=P_э²;

Д[P]= P_э²- P_c²; Р_э- эф­фек­тив­но­го (сре­де­к­вад­ра­тич­но­го зна­че­нии).

Сред­не­квад­ра­тич­ное от­кло­не­ние или стан­дарт на­груз­ки:

где k_ф=Р_э/Р_с – ко­эф­фи­ци­ент гра­фи­ка на­гру­зок.

Груп­по­вая на­груз­ка яв­ля­ет­ся сум­мой ин­ди­ви­ду­аль­ных на­гру­зок, по тео­рии Ля­пу­но­ва при чис­ле эл.при­ем­ни­ков стре­мя­щим­ся к бес­ко­неч­но­сти, но на прак­ти­ке >5. За­кон рас­пре­де­ле­ния слу­чай­ной на­груз­ки под­чи­ня­ет­ся нор­маль­но­му за­ко­ну. Этот за­кон оп­ре­де­ля­ет­ся зна­че­ни­ем сред­ней на­груз­ки (Р_с) и сред­не­квад­ра­тич­ным от­кло­не­ни­ем (σ) – стан­дарт­ным на­пря­же­ни­ем. Прак­ти­че­ски за­кон под­твер­жда­ет­ся при чис­ле эл.при­ем­ни­ков >5.

В со­от­вет­ст­вии с ука­зан­ным за­ко­ном рас­пре­де­ле­ния на­гру­зок мо­жет при­ни­мать сколь угод­но боль­шие зна­че­ния при этом ве­ро­ят­ность этих зна­че­ний мо­жет при­ни­мать сколь угод­но ма­ло, но от­лич­но от ну­ля. Это рас­хо­дит­ся с дей­ст­ви­тель­но­стью. Т.к. на­ру­ша­ет­ся за­кон фи­зи­че­ской реа­ли­зуе­мо­сти. В свя­зи с этим ог­ра­ни­че­ни­ем ма­лые ве­ро­ят­но­сти мень­ше не­ко­то­рой ве­ли­чи­ны λ при­ни­ма­ют в рас­че­тах = 0. Так, на­при­мер, в очень точ­ных рас­че­тах (ис­сле­до­ва­ни­ях) мож­но пре­неб­речь зна­че­ни­ем λ<0.005. В ме­нее точ­ных рас­че­тах λ=0.05.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: