Построение интервального вариационного ряда

1. Разбива­ют множество значений вариант на полуинтервалы т.е. производят их группировку.

Рекомендуется количество интер­валов k выбирать по формуле Стерджерса

(1.4)

Длина интервала равна

Δ = x_max – x_min/ k

Замечание 1.

В литературе предлагается и такая форма записи формулы Стерджерса

1. Рекомендуемое число интервалов

2. Величина интервала:

3. Строим интервал: за начало 1-го интервала берут:

 

2. Считают число вариант, попавших в полуинтервал .

Получают значения частот , .

3. Интер­вальный ряд можно представить таблицей (табл. 1.2):

Таблица 1.2

Варианты			…
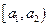
Частоты			…

 

Замечание 2.

Если варианта находится на границе интервала, то ее при­соединяют к правому интервалу.

 

Графические изображения вариационных рядов

 

Для наглядности представления используют графические изображения вариационных рядов в виде:

- полигона;

- гистограм­мы;

- кумулянты.

Полигон, как правило, служит для изображения дискретно­го вариационного ряда.

Представляет собой ломаную, соединяющую точки плоскости с координатами .

Для интервального ряда также строится полигон, только его ломаная проходит через точки , где .

Гистограмма служит только для представления интерваль­ных вариационных рядов и имеет вид ступенчатой фигуры из прямоугольников с основаниями, равными длине интервалов Δ, и высотами, равными частотам интервалов.

Кумулянта представляет собой ломаную, соединяющую точки с координатами (где — накопленные часто­ты) для дискретного ряда, или точки с координатами 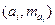для интервального ряда.

Эмпирической функцией распределения 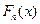называется функция, значение которой в точке х равно накопленной час­тоте, т.е.

(1.6)

 

Для интервального ряда указываются не конкретные значения вариант, а только их частоты на интервалах. В этом случае эм­пирическая функция распределения определена только на кон­цах интервалов. Ее можно изобразить ломаной, проходящей через точки .

Эмпирической плотностью распределения непрерывного ва­риационного ряда называется функция

 

, если

 

, если или
Функция 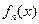является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.

 

Практический материал

Пример 1.1. В магазине за день было продано 45 пар муж­ской обуви.

Имеется выборка значений случайной величины X — разме­ра обуви:

39, 41, 40, 42, 41, 40, 42, 44, 40, 43, 42, 41, 43, 39, 42,

41, 42, 39, 41, 37, 43, 41, 38, 43, 42, 41, 40, 41, 38, 44,

40, 39, 41, 40, 42, 40, 41, 42, 40, 43, 38, 39, 41, 41, 42.

Построить:

1. Дискретный вариационный ряд.

2. Полигон.

3. Куму­лянту.

4. Эмпирическую функцию распределения.

Решение.

1. Для построения вариационного ряда различные значения признака располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту (табл. 1.3).

Таблица 1.3

2. Полигон этого распределения изображен на рис. 7.1.

 

36 37 38 39 40 41 42 43 44 45 x

3. По данным табл. 1.3 находим накопленные частоты и частости (табл. 1.4).

Таблица 1.4

		0,022	0,089	0,2	0,378	0,644	0,844	0,956

 

На рис. 7.2 изображена кумулянта, а на рис. 7.3 – эмпирическая функция распределения.

Кумулянта

Эмпирическая функция распределения

 

Пример 1.2. Результаты измерений отклонений от номинала диаметров 50 подшипников дали численные значения (в мкм), приведенные в табл. 1.5.

Таблица 1.5

 

-1,752	-0,291	-0,933	-0,450	0,512
-1,256	1,701	0,634	0,720	0,490
1,531	-0,433	1,409	1,730	-0,266
-0,058	0,248	-0,095	-1,488	-0,361
0,415	-1,382	0,129	-0,361	-0,087
-0,329	0,086	0,130	-0,244	-0,882
0,318	-1,087	0,899	1,028	-1,304
0,349	-0,293	-0,883	-0,056	0,757
-0,059	-0,539	-0,078	0,229	0,194
-1,084	0,318	0,367	-0,992	0,529

 

Для данной выборки построить:

1. Интервальный вариацион­ный ряд.

2. Полигон.

3. Гистограмму.

4. График эмпириче­ской функции распределения.

5. График эмпирической плотности рас­пределения.

 

 

Решение.

1. По данным табл. 1.5 определяем ; .

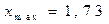2. Разобьем множество значений выборки на интерва­лы. Число интервалов по формуле (1.4) равно

3. Выберем:

- число интервалов k = 7;

- начало первого интервала ;

- конец последнего, седьмого, интервала .

4. Варианту отнесем в первый интервал.

5. Длина каждого интер­вала будет равна

6. Подсчитаем число вариант, попадающих в каждый интер­вал. Получим вариационный ряд (табл. 1.6).

Таблица 1.6

 

 

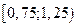
7. По данным табл. 1.6 строим полигон и гистограмму (рис. 7.4).

7. Строим эмпирическую функцию распределения.

Для этого вы­числим накопленные частоты (табл. 1.7).

Таблица 1.7

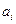
	–1,75	–1,25	–0,75	–0,25	0,25	0,75	1,25	1,75
		0,1	0,26	0,44	0,68	0,86	0,92
пояснение	0/50=0	5/50=0,1	13/50=0,26	22/50=0,44	и т.д.

 

8. По формуле (1.7) вычислим значения эмпириче­ской плотности вероятности для каждого интервала (табл. 1.8).

Таблица 1.8

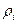
	0,2	0,32	0,36
пояснение	5/(50∙0,5)=0,2	8/(50∙0,5)=0,32	9/(50∙0,5)=0,36

 

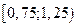
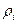
	0,48	0,36	0,12	0,16
пояснение	и т.д.

 

На рис. 7.5 изображена эмпирическая функция распределе­ния, а на рис. 7.6 — эмпирическая плотность.

 

 

 

Лабораторная работа 2

Числовые характеристики

Вариационных рядов

Основная характеристика вариационного ряда – это средняя арифметическая, которая также называется выборочным средним.

Для дискретного выборочного ряда средняя арифметическая равна

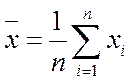. (1)

Для интервального ряда

(2)

В последней формуле за принимают середину 1-го интервала.

Свойства средней арифметической:

1) Если , то .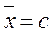

2) Если все варианты умножить на одно и то же число, то средняя арифметическая умножается на то же число:

3) Средняя арифметическая отклонений вариант от средней равна нулю.

4) Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:

 

5) Если ряд состоит из нескольких групп, то общая средняя арифметическая равна средней арифметической групповых средних, причем весами являются относительные объемы групп:

где 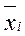— групповые средние,

— объемы групп,

— число групп.

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: