 |
Показатели рассеивания (вариации) признака
|
|
|
|
Показателем вариации является вариационный размах R:
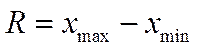
Более содержательными являются меры рассеивания вариант вокруг своих средних величин.
Средним линейным отклонением вариационного ряда называется величина
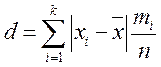
Чаще всего в статистических исследованиях мерой рассеивания служит выборочная дисперсия.
Выборочной дисперсией называется средняя арифметическая квадратов отклонений вариант от их выборочной средней:
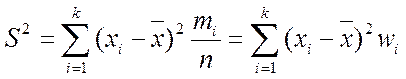(3)
Для несгруппированного ряда (mi = 1) выборочная дисперсия равна
Дисперсию 
часто называют эмпирической или выборочной, подчеркивая, что она (в отличие от дисперсии случайной величины) находится по опытным или статистическим данным.
Для практических вычислений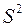 
более удобной является следующая формула:
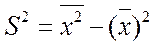
Свойства выборочной дисперсии:
1) Дисперсия постоянной равна нулю.
2) Если ко всем вариантам добавить постоянное число, то дисперсия не изменится.
3) Если все варианты умножить на одно и то же число 
, то дисперсия умножится на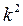 
.
4) Правило сложения дисперсий:
Обозначим через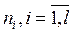 
, количество различных вариант в i-й группе, через 
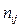— частоту j-й варианты в этой группе.
Тогда i-я группа ряда записывается в виде 
, при этом значение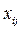 
повторяется 
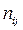раз. Обозначим через 
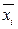групповые средние арифметические:
Групповые дисперсии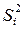 
равны
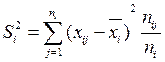
Ряд может состоять из нескольких групп наблюдений.
Средняя арифметическая групповых дисперсий равна
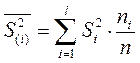
Межгрупповая дисперсия равна
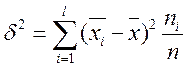
Правилом сложения дисперсий называется равенство
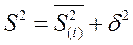
Это равенство служит основой для дисперсионного анализа
Мерой вариации признака является выборочное среднее квадратическое отклонение, которое определяется как корень из дисперсии:
|
|
|
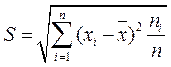(4)
В статистическом анализе рассматривается также коэффициент вариации, равный процентному отношению выборочного среднего квадратического отклонения к выборочной средней:
Упрощенный способ вычисления
средней арифметической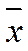 
и выборочной дисперсии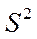 
Введем новые варианты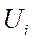 
, по формуле
, (5)
где C и h специально подобранные константы.
Вычислив среднее арифметическое 
и выборочную дисперсию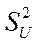 
для вариант 
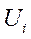, находим затем 
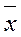и 
:
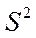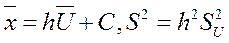(6)
Формулы (5) и (6) дадут заметное упрощение расчетов, если:
для интервального ряда в качестве h взять длину Δ интервала, а в качестве С — середину вариационного ряда.
Пример 1. В табл. 1приведены данные об урожайности ржи на различных участках поля.
Таблица 1
| Урожай-ность ржи, ц/га | [9-12] | [12-15] | [15-18] | [18-21] | [21-24] | [24-27] |
| Доля участка в общей площади, % |
Найти выборочную дисперсию, коэффициент вариации и размах вариации признака X, обозначающего «урожайность ржи».
Решение. Выборочное среднее по формуле (2) равно
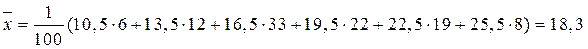
Комментарий: (9 +12)/2 =10,5
По формуле (3) вычислим выборочную дисперсию:
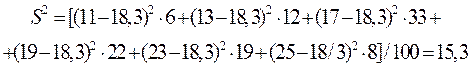
Тогда S =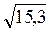 
=3,9 и коэффициент вариации по формуле (4) равен
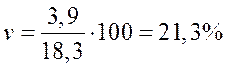
Размах вариации
R = 27 – 9 = 18
Пример 2. Выполнение норм выработки рабочих характеризуется данными, приведенными в табл. 2. Найти средний процент выполнения норм выработки, дисперсию и коэффициент вариации.
Таблица 2
| Процент выполнения норм выработки, % | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 |
| Число рабочих |
Решение. Для упрощения расчетов введем новые варианты 
, где С = 115, h = 10. Тогда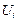 
принимают значения 
Комментарий: (95 - 115)/10 = -2
и
Пример 3. В табл. 3 приведено распределение n = 50 рабочих по производительности труда X (единиц за смену), разделенных на две группы. Найти общие и групповые средние и проверить «правило сложения дисперсий».
Таблица 3
| Прошедшие техническое обучение (группа 1) | Не прошедшие техническое обучение (группа 1) | |||||||||
| ||||||||||
|
|
|
|
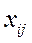
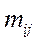
Решение. Для вычисления средних и дисперсий введем новые варианты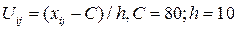 
. Тогда распределение U задается таблицей (табл. 4).
Таблица 4
| -4,6 | 0,5 | 1,6 | 2,2 | 2,3 | -1,7 | -1,1 | 0,3 | 0,9 | 2,6 |
|
|
|
|
