 |
Прямые линии и точки в плоскости
|
|
|
|
Прямая линия принадлежит плоскости, если:
а) она проходит через две точки этой плоскости (рисунок 3а);
б) следы прямой лежат на одноименных следах плоскости (рисунок 3б - частный случай п.1);
в) она проходит через произвольную точку заданной плоскости параллельно любой прямой этой плоскости (рисунок 3в).
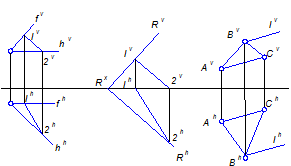
А) б) в)
Рисунок 3
Главные линии плоскости
Это прямые:
Горизонталь, h - это прямая, лежащая в плоскости заданной и параллельная горизонтальной плоскости проекций (рисунки 4 а, б, в).
Фронталь, f – прямая, лежащая в заданной плоскости и параллельная фронтальной плоскости проекций (рисунок 4).

А) б) в) г)
Рисунок 4
Линия наибольшего ската, 1-2 ( рисунок 4 г) – прямая, принадлежащая заданной плоскости и перпендикулярная к её горизонталям и фронталям. Прямой угол, составленный л.н.с. плоскости с ее горизонталью, проецируется на горизонтальную плоскость без искажения.
Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.
Задача
Указать, какие из заданных на чертеже точек, принадлежат плоскости Р.

Рисунок 5
Проверьте себя:
1. Что представляет собой плоскость?
2. Что является определителем плоскости?
3. Сколько существует способов задания плоскостей? Назовите их.
4. Какие положения относительно плоскостей проекций может занимать в пространстве плоскость?
5. Условия принадлежности прямой плоскости.
6. Условия принадлежности точки плоскости.
7. Что представляют собой главные линии плоскости?
Лекция 4
Взаимное положение плоскостей в пространстве
|
|
|
Плоскости могут быть между собой параллельны, могут пересекаться и, как частный случай пересечения, могут быть перпендикулярны друг к другу (см. соответственно рисунок 5 – а, б и с).

Рисунок 5
Если плоскости параллельны между собой, то одна из них проходит через прямую, параллельную этой плоскости. Одноименные следы таких плоскостей параллельны между собой.
Задача 1. Через точки А и В провести плоскости Р (Рн, Рv) и Р(m∩n) параллельную плоскости (рисунок 6).

Рисунок 6 Рисунок 7
Задача 2
Проверить, параллельны ли между собой плоскости b (f ∩ h) и S (m∩n) (рисунок 7).
Пересекающиеся плоскости.
Чтобы построить линию пересечения двух плоскостей, необходимо определить их две общие точки. Или одну общую точку и через нее провести прямую параллельно любой прямой другой плоскости.
Если обе плоскости заданы следами, то общие точки находят на пересечении одноименных следов (рисунок 8 а, б, в, г,). В других случаях вводятся вспомогательные плоскости – посредники (8 е).
Задача 3
Построить линии пересечения двух плоскостей.

А) б) в) г) д) е)
Рисунок 8
Лекция 5
Прямая и плоскость
Прямая может быть параллельна плоскости (как частный случай принадлежать ей) и может пересекать ее, в том числе и под прямым углом.
Прямая, параллельная плоскости
Если прямая параллельна любой прямой плоскости, то она параллельна и самой плоскости (рисунок 8).

Рисунок 8
Точка встречи прямой и плоскости
Чтобы определить точку встречи прямой и плоскости, необходимо:
1) заключить прямую в плоскость, т.е. через заданную прямую провести плоскость, которой она бы принадлежала (рисунок 9).

Рисунок 7
2) построить линию пересечения этих плоскостей
3) на пересечении заданной прямой и линии пересечения и будет находиться искомая точка.
|
|
|
Примеры

Рисунок 10
3. Прямая перпендикулярная плоскости
Прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.
Чтобы провести перпендикуляр к плоскости на эпюре, необходимо из фронтальной проекции точки провести перпендикуляр на фронтальную проекцию фронтали (или фронтальный след), а из горизонтальной проекции - перпендикуляр на горизонтальную проекцию горизонтали (или горизонтальный след плоскости, который, собственно и является нулевой горизонталью).
Для нахождения точки встречи перпендикуляра с плоскостью, необходимо воспользоваться правилом, ранее рассмотренным, для нахождения точки встречи прямой и плоскостью.
Задача 1
Из точки А. опустить перпендикуляр на пл. Р.

Рисунок 11
Задача 2
Из точки А плоскости Р восстановить перпендикуляр и, выбрав на нем произвольную точку, определить ее расстояние до этой плоскости.

Рисунок 12
Плоскость, перпендикулярна к другой тогда, когда она проходит через прямую, перпендикулярную к этой плоскости (рисунки 13 а и в).
|
|
|


