 |
Построение напорной и пьезометрической линий трубопровода
|
|
|
|
Цели работы:
· Изучение уравнения Бернулли;
· Уяснение физической сущности полного напора и составляющих его скоростного (динамического), пьезометрического и геометрического напоров;
· Экспериментальное определение напорной и пьезометрической линий трубопровода.
Теоретические основы:
Уравнение Бернулли играет важнейшую роль в гидравлике. Оно необходимо для решения целого ряда практических инженерных задач.
Для струйки вязкой несжимаемой жидкости при установившемся движении уравнение Бернулли имеет вид:
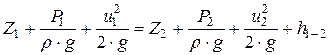
| (5) |
где Z1 - высоты расположения центра тяжести поперечного сечения струйки 1-1;
Z2 - высоты расположения центра тяжести поперечного сечения струйки 2-2;
P1 - давления в центре тяжести сечения 1-1;
P2 - давления в центре тяжести сечения 2-2;
u1 - скорости течения жидкости в сечение 1-1;
u2 - скорости течения жидкости в сечение 2-2;
ρ - плотность жидкости;
h1,2 - потеря напора при перемещении жидкости из сечения 1-1 в сечение 2-2.
Величина 
называется полным гидравлическим напором струйки в соответствующем сечении.
Слагаемые напора:
- геометрическая высота или геометрический напор;
- пьезометрическая высота или пьезометрический напор;
- скоростная высота или скоростной напор;
- гидростатический напор.
Для потока вязкой несжимаемой жидкости уравнение Бернулли записывается в виде:
| (6) |
где υ1 - средние скорости потока жидкости в сечении 1-1;
υ2 - средние скорости потока жидкости в сечении 2-2;
α - коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении. Его величина зависит от формы эпюры скорости и всегда больше единимы. Для ламинарного течения в круглых трубах α =2, для турбулентного течения коэффициент Кориолиса обычно принимает значение в пределах α = 1,05 - 1,1.
|
|
|
Для определения средней скорости потока υ в сечении необходимо использовать одно из основных уравнений гидродинамики - уравнение неразрывности (постоянство объемного расхода вдоль потока несжимаемой жидкости):
| (7) |
где S1, S2 -площади сечений потока.
Из уравнений (5) и (6) следует, что все члены уравнения Бернулли имеют линейную размерность. Однако им можно придать и энергетический смысл.
Действительно, если масса жидкости m поднята на высоту Z над некоторой плоскостью (плоскостью сравнения), то в поле силы тяжести она обладает потенциальной энергией положения тgZ. Отнеся эту энергию к весу жидкости, найдем, что величина Z представляет собой удельную потенциальную энергию положения. - удельная потенциальная энергия давления жидкости, так как частица жидкости массой m при давлении P обладает способностью подняться на высоту и приобрести энергию положения тg (если отнести эту величину к весу жидкости тg, то получим ); - удельная кинетическая энергия жидкости. Следовательно, полный гидродинамический напор потока 
представляет собой полную удельную механическую энергию потока жидкости в данном сечении, а величина h1-2 - уменьшение удельной механической энергии потоки на участке между сечениями 1-1 и 2-2, происходящее в результате работы сил вязкостного трения, сопровождающейся необратимым переходом части механической энергии в тепловую. Таким образом, энергетический смысл уравнения Бернулли для потока (струйки) реальной жидкости заключается в том, что оно является уравнением баланса энергии с учетом потерь. Если на участке потока уменьшается скорость (кинетическая энергия), то, согласно уравнению Бернулли, на этом участке должно соответственно возрасти давление (потенциальная энергия).
|
|
|
Экспериментальная часть:
Объектом исследования является участок трубопровода аб (внутренний диаметр трубопровода - 6 мм). К пяти сечениям трубопровода подключены манометры.
Для проведения эксперимента необходимо:
1. включить питание стенда;
2. включить, нажав кнопку «Пуск», электродвигатель;
3. тумблер Р1 переключить в верхнее положение;
4. дать возможность поработать стенду в течение 5 – 6 минут;
5. для двух значений расхода (настроек регулятора расхода РР) произвести измерения давлений (по манометрам МН1-МН5). Также необходимо уже описанным выше способом измерить расход и температуру рабочей жидкости.
После проведения экспериментов необходимо отключить питание секундомера, выключить электродвигатель и отключить питание стенда.
Обработка результатов опыта:
1. Определяем расходы жидкости:
| (8) |
2. Рассчитываем средние скорости потока в каждом сечении:
| (9) |
3. Определяем кинематическую вязкость масла:
| ν = 11,8·10-6 (50/ Т)1,79 | (10) |
4. Определяем числа Рейнольдса Re по формуле:
| (11) |
5. По величинам Re определяем режимы течения жидкости и значения коэффициента α.
6. Находим пьезометрические напоры.
7. Находим скоростной напор для первого сечения.
8. Рассчитываем полный напор для данного режима течения.
9. Пренебрегая потерями напора в выражении (6), т.е. считая H=const, рассчитываем значения скоростных напоров в остальных сечениях трубопровода.
10. Строим диаграммы геометрического, пьезометрического, скоростного и полного напоров для двух значений расхода в зависимости от расстояния l от первого сечения вдоль трубы.
Таблица 2
| № сеч. | 5 | Примечание | ||||
| Z, м | ρ =920кг/м2 | |||||
| l, м |
Таблица 3
| № | W, м3 | Q, м3/с | Р1, МПа | Р2, МПа | Р3, МПа | Р4, МПа | Р5, МПа | tж, ºC | t, с | V, м/с | ν, м2/с |
Таблица 4
| № | P1/ρg, м | P2/ρg, м | P3/ρg, м | P4/ρg, м | P5/ρg, м |
Таблица 5
| № | Re | Режим течения | α | αV12/2g, м | Н, м | αV22/2g, м | αV32/2g, м | αV42/2g, м | αV52/2g, м |
|
|
|
Отчет по работе
Отчет по работе выполняется по прилагаемой форме на листе форматом А4. На обратной стороне листа приводится пример расчета для одного из опытов.
Лабораторная работа № 3
|
|
|
