 |
Определение коэффициентов местных гидравлических сопротивлений
|
|
|
|
Цели работы:
· Изучение видов и причин потерь энергии в местных гидравлических сопротивлениях;
· Изучение методики экспериментального определения коэффициентов местных гидравлических сопротивлений;
· Экспериментальное определение коэффициента местного гидравлического сопротивления обратного клапана КО1, колена (поворот на 90°), гидродросселя ДР1 (местные сопротивления расположены на участке трубопровода аб с внутренним диаметром трубопровода 6 мм).
Теоретические основы:
Уравнение Бернулли для потока вязкой жидкости запишется в следующем виде:
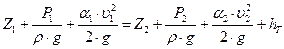
| (12) |
Для практического использования уравнения Бернулли необходимо установить способ определения величин потерь напора hт, вызванных действием в потоке сил сопротивления. Механизм действия этих сил настолько сложен, что до настоящего времени для произвольного движения не удалось найти точного метода вычисления потерь hТ. В технических расчетах чаще всего приходится пользоваться эмпирическими или полуэмпирическими зависимостями.
Как показал опыт прикладной гидродинамики, гидравлические сопротивления удобно разделить на два класса, или вида. Первый вид - это сопротивления, связанные с трением потока жидкости о стенки трубы. Потери в этом случае равномерно распределены по длине потока и называются потерями по длине hλ. Этот вид потерь в чистом виде может иметь место только в потоке с постоянной по его длине средней скоростью. Такие потоки называются равномерными: они могут существовать лишь в прямой цилиндрической трубе или призматическом канале.
С другим видом гидравлических сопротивлений, а следовательно, и потерь мы встречаемся в случаях резких изменений формы граничных поверхностей потока на коротком участке. Потери здесь вызываются деформацией потока пограничными поверхностями, сопровождающейся перестройкой закона распределения скоростей и образованием зон с вихревым движением жидкости. Такие участки резких деформаций потока называют местными гидравлическими сопротивлениями, а вызванные ими потери - местными потерями напора hм.
|
|
|
Наряду с различием конфигураций граничных поверхностей необходимо учитывать влияние режимов движения жидкости на величину и механизм потерь, т.е. важно знать условия перехода ламинарного течения в турбулентное. В реальных конструкциях участки равномерного движения жидкости могут чередоваться с местными сопротивлениями, число частных видов которых чрезвычайно велико. При подсчетах полных потерь напора широко применяется принцип сложения, согласно которому полные потери равны сумме потерь на отдельных участках равномерного движения и потерь на всех местных сопротивлениях:
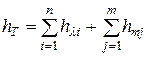
| (13) |
где hλi - потеря по длине на i -м участке равномерного движения;
hλj - местные потери на j -м местном сопротивлении.
При протекании жидкости через местное сопротивление в потоке возникают деформации эпюры скоростей, отрывы и вихревые зоны, которые могут распространяться как вверх, так и вниз по течению. В связи с этим, если величины hmj вычисляют по формулам, установленным для изолированных местных сопротивлений, то применение принципа сложения потерь согласно (13) будет правомерным лишь в том случае, когда местные сопротивления не влияют друг на друга, т.е. разделены участками движения со стабилизированным распределением скоростей. В противном случае два или более местных сопротивления следует рассматривать как одно сложное и для него должны быть, установлены специальные расчетные зависимости.
Исходя из общих законов гидродинамики, можно установить структуру общих формул, выражающих потери в любом сопротивлении. Из этих общих формул в некоторых случаях удается получить теоретические формулы для конкретных видов сопротивлений, а в других случаях приходится, пользуясь опытными данными, конкретизировать формулы эмпирическими коэффициентами. Общая формула потерь в гидравлическом сопротивлении называется формулой Вейсбаха и имеет вид:
|
|
|
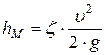
| (14) |
В общем случае коэффициент местного гидравлического сопротивления ζМ зависит от пограничной геометрии и числа Рейнольдса, и его можно представить в виде:
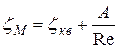
| (15) |
где А - константа, зависящая от формы сопротивления и числа Rе.
Из этой формулы вытекает, что при малых числах Rе второй член правой части, т.е. А/Rе,играет определяющую роль в величине ζМ.
А при возрастания числа Rе этот член становится малым и, следовательно, число Rе,а значит и вязкость, перестают влиять на величину ζМ. При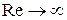 
значение 
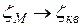. Индекс «кв»означает квадратичность сопротивления, т.е. пропорциональность потерь квадрату скорости, так как ζкв от числа Rе не зависит. Формулу (14) можно использовать и для расчета потерь по длине, если обозначить:
| (16) |
где λ - коэффициент трения по длине трубы;
l - длина трубы;
d - диаметр трубы.
Данные о коэффициентах местных сопротивлений, наиболее часто встречающихся в инженерной практике, приводятся в гидравлических справочниках.
В лабораторной работе потеря напора на местном сопротивлении hм определяется из уравнения Бернулли (12), записанного для каждого из исследуемых местных сопротивлений. Выражая коэффициент местного сопротивления из формулы (14), необходимо учитывать, что если сечение трубопровода меняется, то в формулу (13) подставляют один из скоростных напоров: в сечении до местного сопротивления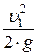 
или в сечении после него 
.
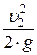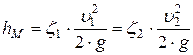
| (17) |
В справочниках указывается, к какому скоростному напору отнесен коэффициент местного сопротивления.
Экспериментальная часть:
Объектами исследований на стенде являются местные гидравлические сопротивления, установленные на участке трубопровода аб между манометрами МН1 - МН5.
Для проведения экспериментов необходимо:
|
|
|
- включить питание стенда;
- включить питание электродвигателя;
- включить тумблер Р1 в верхнее положение.
Дать возможность установке поработать в течение 5 - 6 минут.
Провести при различных расходах 4 - 5 опытов. В каждом опыте измерять по манометрам МН1 - МН5 давления, время прохождения через расходомер заданного объема рабочей жидкости и температуру жидкости.
После выполнения всех опытов отключить питание электронного секундомера, электродвигателя и стенда.
Обработка результатов опыта:
1. Определить расход жидкости:
| (18) |
2. Из уравнения расхода найти среднюю скорость потока до и после каждого сопротивления:
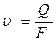
| (19) |
где F - площадь входного и выходного сечений трубопровода.
3. По температуре масла Т определить кинематический коэффициент вязкости по формуле (3).
4. Найти потери напора на местных сопротивлениях по уравнению Бернулли (12) учитывая, что скоростные напоры в рассматриваемых сечениях постоянны.
5. Вычислить коэффициенты местных сопротивлений по формуле (14).
6. Результаты расчетов занести в таблицу 6.
Таблица 6
| № | P1, МПа | P2, МПа | P3, МПа | P4, МПа | P5, МПа | t, с | T, oC | Q, л/с | v, м/с | ||||
Продолжение таблицы 6
| № | hм12, м | hм23, м | hм45, м | ζ12 | ζ23 | ζ45 |
Отчет по работе
Отчет по работе выполняется по прилагаемой форме на листе форматом А4. На обратной стороне листа приводится пример расчета для одного из опытов.
Лабораторная работа № 4
|
|
|
