 |
Определение коэффициента гидравлического трения (коэффициента Дарси)
|
|
|
|
Цели работы:
· Изучение способов определения коэффициента гидравлического трения;
· Изучение методики экспериментального определения коэффициента гидравлического трения;
· Экспериментальное определение коэффициента гидравлического трения и установления зависимости его от числа Рейнольдса.
Теоретические основы:
Потери напора h на участке трубопровода в общем случае определяются из уравнения Бернулли:

| (20) |
где Z1 – геометрическая высота сечения 1-1;
Z 2 – геометрическая высота сечения 2-2;
 - пьезометрический напор в сечении 1-1;
- пьезометрический напор в сечении 1-1;
 - пьезометрический напор в сечении 2-2;
- пьезометрический напор в сечении 2-2;
υ1 - средняя скорость потока в сечении 1-1;
υ 2 - средняя скорость потока в сечении 2-2;
α1 - коэффициент Кориолиса в сечение 1-1;
α2 - коэффициент Кориолиса в сечение 2-2;
Исследуемый участок трубопровода представляет собой отрезок прямой горизонтальной трубы постоянного диаметра, поэтому потери на трение является единственным видом потерь напора на этом участке. Кроме того, 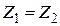 и υ1 = υ2, а значит и α1 = α2, поэтому из уравнения (20) следует, что потери на трение на исследуемом участке:
и υ1 = υ2, а значит и α1 = α2, поэтому из уравнения (20) следует, что потери на трение на исследуемом участке:
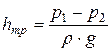
| (21) |
Потери напора на трение определяются по формуле Дарси:

| (22) |
Коэффициент λ называют коэффициентом гидравлического трения. Исследования показали, что для ламинарных потоков в трубах:

| (23) |
где А - константа, зависящая от формы сечения трубопровода. Для круглой трубы А =64, а число Рейнольдса определяется по формуле:

| (24) |
При турбулентных режимах λ зависит от конфигурации потока или, как говорят, от пограничной геометрии, а также от числа Рейнольдса:
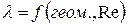
| (25) |
По результатам экспериментов коэффициент λ можно определить с помощью формулы (22), если измерить среднюю скорость υ и потери напора hтр.
|
|
|
Теоретические исследования показали, что согласно (25) следует искать эмпирическую зависимость λ от числа Re икакого-либо безразмерного параметра, определяющего геометрическое подобия потоков. Для гладких круглых труб такого параметра не требуется, поскольку все круглые трубы геометрически подобны и для них экспериментальные точки на графике λ=λ(Re) должны образовать единую кривую. Однако шероховатые трубы не являются геометрически подобными, поскольку требование геометрического подобия должно распространяться не только на форму поперечного сечения, но и, на форму выступов неровностей стенок. Но тогда при строгом подходе практически невозможно найти две геометрически подобные трубы с естественной шероховатостью. В связи с этим в качестве приближенного допущения принимают, что шероховатые трубы будут геометрически подобными, если отношение средней высоты, выступов шероховатости Δ к радиусу ro или диаметру d будет одинаковым. Тогда опытные данные следует обрабатывать в виде кривых:
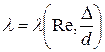
| (26) |
Отношение Δ/d (или Δ/r0) называют относительной шероховатостью, а обратную величину d/Δ – относительно гладкостью.
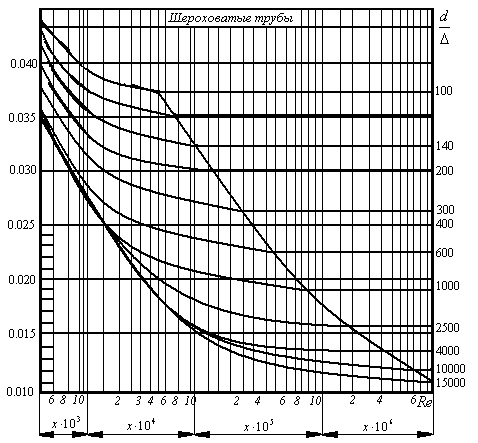
Н. Никурадзе (1933 г.) впервые обработал свои многочисленные опытные результаты указанным способом и построил универсальный график зависимости (17) приведенный на рисунке 3. Шероховатость в опытах Никурадзе создавалась искусственно путем наклеивания калиброванных песчинок на внутреннюю поверхность трубы. Такая шероховатость получалась равнозернистой, чем существенно отличалась от естественной шероховатости труб, образующейся в результате коррозии, отложений и т.п.
Рассмотрим подробно график Никурадзе:
1 - зона ламинарного режима, изображенная прямой. Здесь точки, относящиеся к опытам с разной шероховатостью, ложатся на одну прямую, уравнением которой является зависимость:
|
|
|

| (27) |
|

Границей служит значение абсциссы lg(2300)=lg(Reкр).
Таким образом, данная закономерность имеет место при Re ≤ Reкр, т.е. при ламинарном режиме движения.
В диапазоне чисел Re=2300¸4000 осуществляется переход от ламинарного течения к турбулентному. В потоке наблюдается неустойчивость, порождаемая периодическим возникновением очагов турбулентности и их исчезновением.
2 - зоне гладкостенного течения, образуемая опытными точками, расположенными вдоль другой прямой. Здесь λ также не зависит от шероховатости:

| (28) |
Границей зоны ориентировочно могут служить значения:

| (29) |
Строение потока в пределах гладкостенной зоны можно представить в виде: турбулентного ядра потока и вязкого подслоя в близи стенки, движения в котором преимущественно ламинарное. Толщина подслоя δл достаточна, чтобы покрыть все неровности стенки, благодаря чему движение турбулентного ядра потока происходит как бы в гладкой трубе. Трубы, работающие в таком режиме, называют гидравлически гладкими.
3 - доквадратичная зона сопротивления, которая ограничивается линией гладкостённого режима и штриховой линией К-К, образованной точками, отделяющими горизонтальные участки кривых. В зоне 3 каждая кривая отвечает определенному значению относительной гладкости. Здесь λ зависит от числа Rе и относительной гладкости трубы d/Δ:

| (30) |
Границами зоны приближенно служат значения:
 <Re <Re  . .
| (31) |
4 - зона квадратичного сопротивления, образуемая горизонтальными участками кривых. В этой зоне коэффициент λ не зависит от Rе,т.е.:

| (32) |
Эта зона имеет место при:
Re> 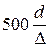
| (33) |
Толщина вязкого подслоя здесь весьма мала, и выступы шероховатости полностью взаимодействуют с турбулентным ядром потока.
График Никурадзе дает общее представление о характере зависимости  для труб с искусственной зернистой шероховатостью Δ. На рисунке 4 даны графики, построенные по результатам опытов с промышленными трубами, проведенных рядом советских исследователей, главным образом Г. А. Муриным во ВТИ им. Ф. Э. Дзержинского. Вид кривых в зоне 3 на графиках Никурадзе и Мурина несколько различен, что объясняют неравномерностью шероховатости естественных труб.
для труб с искусственной зернистой шероховатостью Δ. На рисунке 4 даны графики, построенные по результатам опытов с промышленными трубами, проведенных рядом советских исследователей, главным образом Г. А. Муриным во ВТИ им. Ф. Э. Дзержинского. Вид кривых в зоне 3 на графиках Никурадзе и Мурина несколько различен, что объясняют неравномерностью шероховатости естественных труб.
|
|
|
Таблица7
| Зона сопротивления | Режим течения | Границы зоны | Расчетные формулы | |
| Ламинарный | Re<2320 | 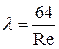
| ||
| Турбулентный гладкостенный | 
|  (Re<105)
(Re<105)

| Для всех турбулентных режимов

| |
| Турбулентный доквадратичный | 
| 
| ||
| Турбулентный квадратичный | 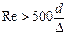
| 

|
Экспериментальная часть:
Коэффициент гидравлического трения определяется на участке трубопровода вг.
Для проведения эксперимента необходимо:
1. Включить питание стенда;
2. Включения питания электродвигателя;
3. Включить тумблер Р1 в нижнее положение.
Дать возможность поработать установке в течение 5-6 минут.
Опыты провести при различных значениях расхода. В каждом опыте необходимо регистрировать по манометрам МН6 и МН7 давления, а также время прохождения через расходомер заданного объема рабочей жидкости и температуру жидкости.
После выполнения всех опытов отключить питание электронного секундомера, электродвигателя и стенда.
|
Обработка результатов опыта:
1. Определить расход жидкости:

| (34) |
2. Из уравнения расхода найти среднюю скорость потока до и после каждого сопротивления:
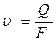
| (35) |
где F - площадь сечения трубопровода.
3. Определить потери напора на трение hтр по уравнению Бернулли.
4. Вычислить опытное значение коэффициента сопротивления λоп, выразив его из формулы (22).
5. По температуре масла найти кинематический коэффициент вязкости ν (см. лабораторную работу 1).
6. Найти число Рейнольдса:

| (36) |
7. По числу Рейнольдса определить режим движения жидкости, при Rе<2320 режим движения считается ламинарным, при Rе>2320 турбулентным.
8. Определить по таблице 1 зону сопротивления и вычислить λТ по выбранной для этой зоны формуле.
9. Найти величину коэффициента λвти по графику ВТИ.
10. Результаты расчетов занести в таблицу 8.
Таблица 8
| № | Р1, МПа | Р2, МПа | W1, м3 | W2, м3 | t, с |
Продолжение таблицы 8
|
|
|
| № | hтр, мм | Q, м3/с | V, м/с | λоп | Re | Режим движения | Зона сопротивления | λТ | λвти |
Отчет по работе
Отчет по работе выполняется по прилагаемой форме на листе форматом А4. На обратной стороне листа приводится пример расчета для одного из опытов.
Лабораторная работа № 5
|
|
|



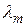 ) от Re для труб с искусственной шерховатостью, построенная Н. Никурадзе.
) от Re для труб с искусственной шерховатостью, построенная Н. Никурадзе.