 |
Импульсные сигналы в радиотехнических устройствах.
|
|
|
|
Сигналы импульсных устройств.
Структура импульсных сигналов.
Для сокращения сигналы импульсных устройств будем называть импульсными.
Импульсная последовательность становится сигналом, когда в соответствии с передаваемой информацией изменяются ее параметры: амплитуда импульсов, их длительность или фаза. В частном случае информация может выражаться появлениемимпульса, изменением его длительности или временного положенияотносительно опорного импульса.
Различают амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ) и фазоимпульсную (ФИМ) модуляции. При каждом виде модуляции один из параметров импульсной последовательности принимает значение, пропорциональное величине непрерывного модулирующего сигнала в момент присутствия импульса.
Рис. 1 иллюстрирует амплитудную модуляцию импульсной последовательности непрерывным сигналом (на рисунке его форма показана пунктиром).
Импульсный сигнал (рис. 1) называют дискретным, так как он составляется элементами — импульсами, действующими в отдельные (дискретные) моменты времени.
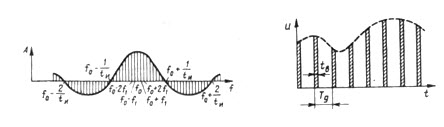
рис. 1
Эти импульсы являются выборками (отсчетами) непрерывного сигнала. Процесс взятия отсчетов называется дискретизацией непрерывного сигнала, а их период — периодом дискретизации.
Вместо передачи непрерывного сигнала можно передавать соответствующий ему дискретный сигнал. В основе этого утверждения лежит теорема отсчетов, сформулированная и доказанная академиком В. А. Котельниковым и ставшая фундаментальным положением теории связи. Суть ее состоит в том, что сигнал, спектр которого не имеет частот выше F m однозначно определяется своими мгновенными значениями (выборками, отсчетами), разделенными одинаковыми интервалами, не превышающими 1/(2 F m). Это означает, что на каждый период наивысшей частотной составляющей сигнала должно быть по меньшей мере два отсчета. Иными словами, частота отсчетов должна по меньшей мере вдвое превышать высшую частоту спектра F m.
|
|
|
Так как амплитуды гармоник сложного колебания уменьшаются с увеличением их частоты, то с некоторой погрешностью всякий спектр можно считать ограниченным, а не бесконечным.
Передачу непрерывного сигнала его выборками можно вести потому, что на приемной стороне канала связи по этим выборкам непрерывный сигнал однозначно восстанавливается фильтром нижних частот, подавляющим все составляющие с частотами выше F m.
Импульсные сигналы в радиотехнических устройствах.
Импульсные сигналы широко используются для передачи информации. Они переносят команды от одного узла устройства к другому, излучаются и принимаются радиолокационными станциями, обеспечивают дистанционное радиоуправление, несут информацию в составе телевизионного сигнала, передают непрерывную информацию в системах импульсной связи и т. д.
При импульсной связи имеется возможность «уплотнить» канал, т. е. одновременно передавать по одному каналу несколько сообщений.
Уплотнение канала состоит в следующем. Так как длительность выборки сигнала (рис. 1)составляет незначительную часть периода дискретизации Tд, то между выборками одного сигнала можно «разместить» выборки других сигналов — по одному каналу связи может одновременно передаваться несколько сигналов. Такой способ одновременной передачи сигналов называется временным уплотнением канала.
При временном уплотнении канала на его передающей и приемной сторонах устанавливаются коммутаторы. Коммутатор на передающей стороне периодически на небольшое время подключает к каналу связи источники непрерывных сигналов, в результате чего в канал поступают выборки то одного, то другого сигнала. На приемной стороне канала устанавливаются фильтры нижних частот, на выходе которых выделяются непрерывные сигналы, восстановленные из поступающих выборок. К этим фильтрам канал связи периодически подключается коммутатором, работающим точно в таком же режиме, что и коммутатор на передающей стороне. В результате к каждому фильтру поступают выборки только одного передаваемого сигнала.
АИМ-сигналы (выборки непрерывного сигнала) могут передаваться непосредственно по проводам. Для передачи таких сигналов через открытое пространство ими модулируется высокочастотное колебание. Полученные радиоимпульсы передаются на приемную сторону канала связи, где в результате детектирования преобразуются в видеоимпульсы — выборки передаваемого непрерывного сигнала. Фильтром низких частот из этих выборок формируется непрерывный сигнал.
|
|
|
Цифровые сигналы
Двоичные числа представляются обычно двумя уровнями напряжения. Например в транзисторно-транзисторной логике (ТТЛ) логическому нулю соответствует напряжение меньше 0,4 В, а логической единице соответствует напряжение от 2,4 В до 5 В. Сигналы двоичных чисел представленные в такой форме называют цифровыми.
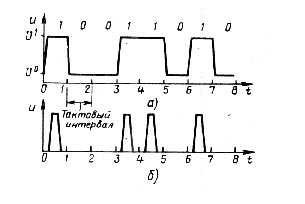
Рис. 2
Цифровой сигнал может быть потенциальным или импульсным.
В потенциальном цифровом сигнале каждый уровень напряжения остаётся неизменным в течение тактового интервала. На рис. 2,а изображен потенциальный цифровой сигнал, представляющий написанное сверху число; высоким потенциалом отображается 1, а низким – 0.
В импульсном цифровом сигнале импульс напряжения представляет 1, а его отсутствие – 0. Такой сигнал изображён на рис. 2,б.
Цифровые сигналы могут представляться в последовательной и параллельной формах.
В последовательной форме разряды числа передаются последовательно друг за другом по одной линии.
В параллельной форме разряды числа передаются одновременно по нескольким линиям, их число равно количеству разрядов числа.
Сигнал представленный в последовательной форме представлен на рис. 1,а и 1,б – в параллельной форме на рис 3.
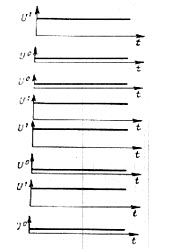
Рис.3
Цифровой сигнал может быть сформирован из непрерывного аналогового сигнала аналого-цифровым преобразователем (АЦП), который называют преобразователем аналог-код или аналог-цифра.
При таком преобразовании из непрерывного сигнала, как показано на рис. 3,а периодически производится выборка мгновенных значений; каждая выборка округляется до ближайшего разрешённого уровня, а код этого уровня (двоичное число) представляется элементами цифрового сигнала. В результате получаем цифровой сигнал, соответствующий непрерывному сигналу.
Такой процесс называют квантованием. Для этого весь диапазон возможных изменений непрерывного сигнала разбивается на конечное число равноотстоящих уровней (называемых уровнями квантования), которые дискретный сигнал только и может принимать. Каждая выборка сигнала округляется до ближайшего разрешённого уровня. Каждому из них может быть присвоен код. Эту операцию называют кодированием. После кодирования операцию над непрерывным сигналом можно заменить операцией над кодами его уровней.
Так, при передаче сигнала (рис. 3,а) надо последовательно в моменты времени t1, t2 …tn передавать информацию о записанных числах. Это осуществляется цифровым сигналом, один элемент которого представляет 1 каждого числа, а другой – 0.
|
|
|
Квантованный дискретный сигнал имеет конечное (счетное) количество значений. Благодаря
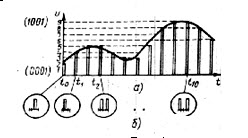
Рис. 4
этому каждому из них может быть присвоен какой-то код (число). Эту операцию называют кодированием.
На рис. 4,б изображен цифровой сигнал, соответствующий квантованному дискретному сигналу (рис. 4,а).
Так как в отношении передаваемой информации цифровой сигнал эквивалентен непрерывному, из которого он сформирован, то вместо операций над непрерывным сигналом (передачи, преобразования, хранения) можно производить операции над соответствующим ему цифровым сигналом. Во многих случаях это оказывается более эффективным.
Обратное преобразование цифрового сигнала в непрерывный осуществляется цифроаналоговым преобразователем (ЦАП). На входы такого преобразователя одновременно поступают потенциалы, представляющие разряды кода каждой выборки. Потенциалы, соответствующие единицам, открывают ключи, через которые на выход поступают напряжения, пропорциональные весам единиц разрядов. Так на выходе формируется напряжение, пропорциональное весу кода каждой выборки.
Устройства, в которых действуют цифровые сигналы, называют цифровыми. Цифровые сигналы используются в устройствах различного назначения. В электронных вычислительных машинах (ЭВМ) и в цифровой автоматике входная информация представляется цифровыми сигналами, над которыми эти устройства осуществляют необходимые действия.
В системах радиосвязи цифровыми сигналами передаются сообщения, имеющие разную форму: звуковую, печатную, форму изображения и т. д. Такая связь отличается скрытностью и помехоустойчивостью.
Последнее обусловлено тем, что такой сигнал имеет только два различимых уровня. Поэтому когда значение сигнала попадает между ними, то это фиксируется как помеха. Если помеха меньше половины разности уровней сигнала, то она легко различается и значения уровней престо восстанавливаются регенераторами.
Непрерывный сигнал очистить от помехи значительно сложнее, что объясняется следующим. Мгновенные значения непрерывного сигнала, разделенные бесконечно малым временным интервалом, отличаются на бесконечно малую величину, т. е. непрерывный сигнал имеет несчетное (бесконечное) количество значений. Поэтому, искаженный помехой, он может быть принят за полезный.
На передающей стороне канала цифровой связи непрерывный сигнал преобразуется в цифровой с помощью аналого-цифрового преобразователя. Цифровой сигнал может непосредственно передаваться по проводам. Для передачи по радиоканалу им модулируется высокочастотное колебание.
На приемной стороне радиоканала цифровой связи принятые радиоимпульсы преобразуются детектором в видеоимпульсы -цифровой сигнал. Этот сигнал может быть использован непосредственно (например, введен в ЭВМ) или преобразован в исходный непрерывный сигнал с помощью цифроаналогового преобразователя.
|
|
|
Импульсы. В большинстве случаев в И. у. используют видеоимпульсы - кратковрем. униполярные изменения тока или напряжения, разделённые паузами (см. также Импульсный сигнал).Различают след, элементы видеоимпульса: резкий подъём (фронт), медленно меняющуюся часть (вершину), быстрый спад (срез), часто завершающийся длинным "хвостом". Иногда после фронта и среза наблюдаются быстро затухающие колебания (двусторонние выбросы). Параметры импульса: размах (амплитуда) А, длительность tи, отсчитываемая на заранее обусловленном уровне (напр., 0,1 A, 0,5А), длительности фронта и среза. Последние обычно отсчитывают между уровнями (0,1-0,9) А. Для нек-рых задач важным параметром является спад или подъём на вершине D A. Если детальная конфигурация импульса не имеет существ, значения, форму видеоимпульсов идеализируют и говорят о прямоугольных, треугольных, трапецеидальных, колокольных (гауссовых) экспоненциальных и др. импульсах. Помимо одиночных н нерегулярно следующих во времени потоков импульсов на практике используют периодпч. последовательности, к-рые дополнительно характеризуют периодом (ср. периодом) Т пли частотой повторения F=T-1. Важным параметром периодич. последовательности является скважность потока Q=T/t и При генерировании мощных видеоимпульсов в промежутках между импульсами (в паузах) производится запасание энергии в накопителях, а её высвобождение - за время tи. При Qд1 в нагрузке реализуются огромные мощности, в Q раз большие средней.
|
|
|
65. Системы счисления.
Системы счисления
Системы счисления - совокупность приемов и правил для записи любого числа с помощью ограниченного количества знаков.
Существующие системы счисления подразделяются на позиционные и непозиционные.
Позиционные системы счисления – такие системы счисления, где значимость числа определяется его местоположением в записи числа.
Любое число Х в позиционной системе счисления с основанием q можно представить в виде полинома:
 (1),
(1),
где q- основание системы счисления – количество цифр, необходимых для записи любого числа,
qi- весовой коэффициент,
хi-разрядный коэффициент.
Разряды с неотрицательными степенями q отражают целую часть числа, а с отрицательными степенями – дробную часть числа.
Примеры позиционных систем счисления: 25(10), Е56(16), 100110(2), 470(8).
При заданном числе разрядов и заданном основании системы счисления, может быть N=qn+m различных наборов чисел.
Непозиционные системы счисления, соответственно, такие системы счисления, где значимость числа не определяется его местоположением в записи числа. Например, римская система записи числа: XXIV, III, VI.
Десятичная система счисления используется человеком в обыденной жизни. При использовании в технике десяти цифр десятичной системы счисления предполагается использование 10 различных уравнений напряжения. В этом случае надо повысить пороги между соседними уровнями напряжения, чтобы не снизить устойчивость к помехам или значительно усложнить устройство распознавания уровней напряжения. Сколько разрядов – столько устройств необходимо.
С другой стороны чем выше q (основание системы счисления), тем меньше надо разрядов (хi) меньше линий, ниже устройств поразрядного анализа.
Однако все же критерием выбора основания системы счисления, используемым в технических системах, является минимизация аппаратных затрат при достижении достаточной помехоустойчивости.
Математические расчеты дали оптимальную величину основания системы счисления q = е» 2.71, что технически реализовать сложно и нецелесообразно.
В технике применяется двоичная система счисления (q=2) c цифровыми знаками 0 и 1.
Так же встречается 8-ричная и 16-ричная система счисления. Само число изображается в 2-ой системе счисления, а адрес числа в 8-ой или 16-ой системе счисления. Пример чисел от 0 до 16 в различных системах счисления представлен в таблице 1.
Таблица 1Пример представления чисел в различных системах счисления
| «10» | «2» | «8» | «16» |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | 0 01 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 | 0 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 20 | 0 01 02 03 04 05 06 07 08 09 A B C D E F 10 |
Разработан ряд правил перевода чисел из одной системы счисления в другую.
Перевод из q –ичной системы счисления в 10 –ую осуществляется по формуле (1).
Пример: 0110,112=0*23+1*22+1*21+0*20+1*2-1+1*2-2=4+1+0,5+0,25=5,7510.
Перевод из 10 –чной системы счисления в q –ичную осуществляется следующим образом:
- целая часть числа делится на основание новой системы счисления до тех пор, пока частное от деления не станет меньше величины основания новой системы счисления. Результат записывается из остатков от деления, начиная с последнего частного.
- дробная часть числа умножается на основание новой системы счисления, целая часть числа отбрасывается, и операция умножения производится до достижения требуемой точности (количества знаков после запятой). Результат записывается из целых частей результатов произведений, производимых сначала.
Пример:

Ответ: 3951910=9A5F16.
Пример:
0,7821502
х 16
12,514403
х 16
8,230448
х 16
3,687168
х 16
10,994688
Ответ: 0.782150210=0,С83А16.
Перевод из 8-чной системы в 2-чную и из 16-чной в 2–чную:
производится из соображений того, что 23=8 и 24=16. Поэтому в исходном 8-чном или 16-чном числе цифры исходного кода заменяются на двоичные 3-х (23=8) или 4-х (24=16) празрядные комбинации.
На том же основан перевод чисел из 2–чной системы счисления в 8-чную и в 16-чную, только теперь данное двоичное многоразрядное число разбивается на группы по 3 или 4 разряда, соответственно, от предполагаемой запятой, разделяющей целую и дробную части двоичного числа.
Алгебра логики.
| Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. |
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Что же такое логическое высказывание?
| Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo. |
Так, например, предложение " 6 — четное число " следует считать высказыванием, так как оно истинное. Предложение " Рим — столица Франции " тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения " ученик десятого класса " и " информатика — интересный предмет ". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие " интересный предмет ". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа " в городе A более миллиона жителей ", " у него голубые глаза " не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
| Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. |
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания. Так, например, высказывание " площадь поверхности Индийского океана равна 75 млн кв. км " в одной ситуации можно посчитать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так, например, из элементарных высказываний " Петров — врач ", " Петров — шахматист " при помощи связки " и " можно получить составное высказывание " Петров — врач и шахматист ", понимаемое как " Петров — врач, хорошо играющий в шахматы ".
При помощи связки " или " из этих же высказываний можно получить составное высказывание " Петров — врач или шахматист ", понимаемое в алгебре логики как " Петров или врач, или шахматист, или и врач и шахматист одновременно ".
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В — высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" — логическая связка, А, В — логические переменные, которые мoгут принимать только два значения — "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием (или знаком  ). Высказывание
). Высказывание  истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна — спутник Земли " (А); " Луна — не спутник Земли " (
истинно, когда A ложно, и ложно, когда A истинно. Пример. " Луна — спутник Земли " (А); " Луна — не спутник Земли " ( ).
).
И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой ". " (может также обозначаться знаками  или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v (или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" — истинны.
ЕСЛИ-ТО Операция, выражаемая связками "если..., то", "из... следует", "... влечет...", называется импликацией (лат. implico — тесно связаны) и обозначается знаком 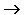 . Высказывание
. Высказывание 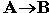 ложно тогда и только тогда, когда А истинно, а В ложно.
ложно тогда и только тогда, когда А истинно, а В ложно.
Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: "данный четырёхугольник — квадрат" (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание 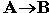 , понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание
, понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание 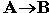 истинно:
истинно:
1. А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
2. А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
3. A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка "если..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США — демократ, то в Африке водятся жирафы", "если арбуз — ягода, то в бензоколонке есть бензин".
РАВНОСИЛЬНО Операция, выражаемая связками " тогда и только тогда ", " необходимо и достаточно ", "... равносильно...", называется эквиваленцией или двойной импликацией и обозначается знаком  или ~. Высказывание
или ~. Высказывание  истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
Высказывания А и В, образующие составное высказывание  , могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" (
, могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" ( ), "пингвины не живут в Антарктиде" (
), "пингвины не живут в Антарктиде" (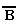 ). Образованные из высказываний А и В составные высказывания A
). Образованные из высказываний А и В составные высказывания A  B и
B и 

 истинны, а высказывания A
истинны, а высказывания A 
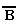 и
и 
 B — ложны.
B — ложны.
Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию можно выразить через дизъюнкцию и отрицание:
А 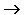 В = В =  v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А  В = ( В = ( v В) . ( v В) . (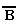 v А). v А).
|
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
Логические операции.
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность  («тогда и только тогда, когда»), импликация
(«тогда и только тогда, когда»), импликация  («следовательно»), сложение по модулю два
(«следовательно»), сложение по модулю два  («исключающее или»), штрих Шеффера
(«исключающее или»), штрих Шеффера  , стрелка Пирса
, стрелка Пирса  и другие.
и другие.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция  приобретает смысл вычитания из единицы;
приобретает смысл вычитания из единицы;  — немодульного сложения; & — умножения;
— немодульного сложения; & — умножения;  — равенства;
— равенства;  — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);
— в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);  — непревосходства суммы над 1 (то есть A
— непревосходства суммы над 1 (то есть A  B = (A + B) <= 1).
B = (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
[править] Свойства логических операций
1. Коммутативность: x  y = y
y = y  x,
x,  {&,
{&,  }.
}.
2. Идемпотентность: x  x = x,
x = x,  {&,
{&,  }.
}.
3. Ассоциативность: (x  y)
y)  z = x
z = x  (y
(y  z),
z),  {&,
{&,  }.
}.
4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
o  ,
,
o  ,
,
o  .
.
5. Законы де Мо́ргана:
o  ,
,
o  .
.
6. Законы поглощения:
o  ,
,
o  .
.
7. Другие (1):
o  .
.
o  .
.
o  .
.
o  .
.
o  .
.
8. Другие (2):
o 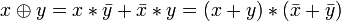 .
.
o  .
.
o  .
.
o 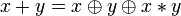
9. Другие (3) (Дополнение законов де Мо́ргана):
o  .
.
o  .
.
Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класк
|
|
|


