 |
Основные законы алгебры логики.
|
|
|
|
Законы алгебры логики базируются на аксиомах и позволяют преобразовывать логические функции. Логические функции преобразуются с целью их упрощения, а это ведет к упрощению цифровой схемы.
АКСИОМЫ алгебры логики описывают действие логических функций "И" и "ИЛИ" и записываются следующими выражениями:
| 0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1 | 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 |
Всего имеется пять законов алгебры логики:
Закон одинарных элементов
1 * X = X
0 * X = 0
1 + X = 1
0 + X = X
Этот закон непосредственно следует из приведённых выше выражений аксиом алгебры логики.
Верхние два выражения могут быть полезны при построении коммутаторов, ведь подавая на один из входов элемента “2И” логический ноль или единицу можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал.
Второй вариант использования этих выражений заключается в возможности избирательного обнуления определённых разрядов многоразрядного числа. При поразрядном применении операции "И" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал. Например, требуется обнулить 6, 3 и 1 разряды. Тогда:

В приведённом примере отчётливо видно, что для обнуления необходимых разрядов в маске (нижнее число) на месте соответствующих разрядов записаны нули, в остальных разрядах записаны единицы. В исходном числе (верхнее число) на месте 6 и 1 разрядов находятся единицы. После выполнения операции "И" на этих местах появляются нули. На месте третьего разряда в исходном числе находится ноль. В результирующем числе на этом месте тоже присутствует ноль. Остальные разряды, как и требовалось по условию задачи, не изменены.
|
|
|
Точно так же можно записывать единицы в нужные нам разряды. В этом случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов. При поразрядном применении операции “ИЛИ” можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды нулевой или единичный потенциал. Пусть требуется записать единицы в 7 и 6 биты числа. Тогда:

Здесь в маску (нижнее число) мы записали единицы в седьмой и шестой биты. Остальные биты содержат нули, и, следовательно, не могут изменить первоначальное состояние исходного числа, что мы и видим в результирующем числе под чертой.
Первое и последнее выражения позволяют использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов. Для этого неиспользуемые входы в схеме “И” должны быть подключены к источнику питания, как это показано на рисунке 1:

Рисунок 1. Схема "2И-НЕ", реализованная на элементе "3И-НЕ".
а неиспользуемые входы в схеме "ИЛИ" должны быть подключены к общему проводу схемы, как это показано на рисунке 2.

Рисунок 2. Схема "НЕ", реализованная на элементе "2И-НЕ".
Законы отрицания
a. Закон дополнительных элементов.


Выражения этого закона широко используется для минимизации логических схем. Если удаётся выделить из общего выражения логической функции такие подвыражения, то можно сократить необходимое количество входов элементов цифровой схемы, а иногда и вообще свести всё выражение к логической константе.
a. Двойное отрицание
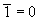



b. Закон отрицательной логики


Закон отрицательной логики справедлив для любого числа переменных. Этот закон позволяет реализовывать логическую функцию "И" при помощи логических элементов “ИЛИ” и наоборот: реализовывать логическую функцию “ИЛИ” при помощи логических элементов “И”. Это особенно полезно в ТТЛ схемотехнике, так как там легко реализовать логические элементы “И”, но при этом достаточно сложно логические элементы “ИЛИ”. Благодаря закону отрицательной логики можно реализовывать элементы “ИЛИ” на логических элементах “И”. На рисунке 3 показана реализация логического элемента “2ИЛИ” на элементе “2И-НЕ” и двух инверторах.
|
|
|

Рисунок 3. Логический элемент “2ИЛИ”, реализованный на элементе “2И-НЕ” и двух инверторах.
То же самое можно сказать и о схеме монтажного “ИЛИ”. В случае необходимости его можно превратить в монтажное “И”, применив инверторы на входе и выходе этой схемы.
Комбинационные законы.
Комбинационные законы алгебры логики во многом соответствуют комбинационным законам обычной алгебры, но есть и отличия.
a. закон тавтологии (многократное повторение)
X+X+X+X=X
X*X*X*X=X
Этот закон позволяет использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов. Например, можно реализовать двухвходовую схему 2И на элементе 3И, как это показано на рисунке 4:

Рисунок 4. Схема “2И-НЕ”, реализованная на элементе “3И-НЕ”.
или использовать схему 2И-НЕ в качестве обычного инвертора, как это показано на рисунке 5:

Рисунок 5. Схема “НЕ”, реализованная на элементе “2И-НЕ”.
Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его ёмкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом.
Для уменьшения числа входов в логическом элементе лучше воспользоваться законом одинарных элементов, как это было показано выше.
a. закон переместительности
A+B+C+D=A+C+B+D
b. закон сочетательности
A+B+C+D=A+(B+C)+D=A+B+(C+D)
c. закон распределительности
X1(X2+X3)= X1X2 + X1X3
X1+X2X3=(X1+X2)(X1+X3)=/ докажем это путём раскрытия скобок/= X1X1+ X1X3+ X1X2+ X2X3= X1(1+X3+X2)+ X2X3= X1+X2X3
|
|
|


