 |
Импульсная и переходная характеристики ситемы. Связь между ними. Интеграл дюамеля. Условие физической реализуемости системы.
|
|
|
|
ФИЗИЧЕСКИЕ СИСТЕМЫ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ: СИСТЕМНЫЕ ОПЕРАТОРЫ, СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СИСТЕМЫ, ЛИНЕЙНЫЕ СИСТЕМЫ.
Системные операторы. Система – совокупность физ. объектов, между которыми существуют опред. взаимодействия. В структуре системы можно выделить вход, на который подается исходный сигнал, и выход, откуда снимается преобразованный сигнал. В наиболее простом случае как входной сигнал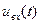 
, так и выходной сигнал 
, называемый также откликом или выходной реакцией системы, описываются одиночными функциями времени. В более общем случае вх. сигнал представляется в виде т -мерного вектора
, а выходной сигнал – в виде п -мерного вектора
.
Закон связи между сигналами 
и 
задают системным оператором Т, результатом возд-я которого на сигнал служит сигнал :
. (1)
Чтобы полностью определить задачу, следует указать область D вх некоторого функц. простр-ва, к-ая называется областью допустимых входных воздействий. Задание этой области описывает х-р вх. сигналов, к-ые могут быть непрерывными, дискретными, детерминированными или случайными. Подобным же образом должна быть указана область D вых допустимых выходных сигналов.
Математической моделью системы наз-ют совокупность сист. оператора Т и двух областей допустимых сигналов D вх, D вых.
Стационарные и нестационарные системы. Принято говорить, что система стационарна, если ее выходная реакция не зависит от того, в какой момент времени поступает вх. сигнал. Если Т – оператор стац. системы, то из рав-ва (1) следует, что
при любом значении t 0. Стац. системы наз-ют также системами с постоянными во времени параметрами.
Если же св-ва системы не инвариантны относительно выбора начала отсчета времени, то такую систему наз-ют нестационарной (системой с переменными во времени параметрами или парам. системой).
|
|
|
Оба указанных класса систем широко прим-ся в радиотехнике.
Линейные системы. Важнейший принцип классификации систем основан на том, что разл. системы по-разному ведут себя при подаче на вход суммы нескольких сигналов. Если оператор системы таков, что справедливы рав-ва
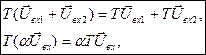(2)
где α – произвольное число, то данная система наз-ся линейной. Условия (2) выражают фундаментальный принцип суперпозиции.
Если эти усл-я не выполняются, то говорят, что система явл-ся нелинейной.
Лин. системы замечательны тем, что, по крайней мере теоретически, можно решить любую задачу о преобразовании вх. сигнала такой системой.
ИМПУЛЬСНАЯ И ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКИ СИТЕМЫ. СВЯЗЬ МЕЖДУ НИМИ. ИНТЕГРАЛ ДЮАМЕЛЯ. УСЛОВИЕ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ СИСТЕМЫ.
Импульсная характеристика. Пусть некоторая лин. стац. система описывается оператором Т, а вх. и вых. сигналы одномерны. По определению, импульсной характеристикой системы наз-ся функция h (t), являющаяся откликом системы на вх. сигнал δ (t), т.е. h (t) удовлетворяет уравнению
. (1)
Поскольку система стационарна, то справедливо следующее:
.
Имп. х-ка, так же как и порождающая ее дельта-функция, есть результат разумной идеализации. С физ. т. зр. имп. х-ка приближенно отображает реакцию системы на вх. имп. сигнал произвольной формы с един. площадью при усл-и, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например периодом ее собств. колебаний.
Интеграл Дюамеля. Зная имп. х-ку лин. стац. системы, можно формально решить любую задачу о прохождении детерм. сигнала через такую систему. Действительно, вх. сигнал допускает представление вида
.
Отвечающая ему выходная реакция 
. (2)
Теперь примем во внимание, что интеграл есть предельное зн-е суммы, поэтому лин. оператор Т на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ. Поэтому из выражения (2) следует, что
|
|
|
, или окончательно 
. (3)
Эта формула называется интегралом Дюамеля (ИД). Она свидетельствует о том, что вых. сигнал лин. стац. системы представляет собой свертку 2-х функций – вх. сигнала и имп. х-ки системы. Очевидно, формула (3) может быть записана также в виде 
.
Условие физической реализуемости. Вых. сигнал, отвечающий импульсному вх. воздействию, не может возникнуть до момента появления импульса на входе.
Отсюда вытекает очень простое ограничение на вид допустимых импульсных характеристик: 
.
Легко видеть, что для физически реализуемой системы верхний предел в формуле ИД может быть заменен на текущее значение времени: 
.
Лиин. стац.система, выполняя обработку поступающего на вход сигнала, проводит опцию взвешенного суммир-я всех его мгн.зн-й, существовавших «в прошлом» при 
.Физически реализуемая система ни при каких обстоятельствах не способна оперировать «будущими» значениями входного сигнала.
Переходная характеристика. Пусть на входе лин. стац. системы действует сигнал, изоб-мый ф-цией Хевисаида σ(t). Выходную реакцию 
принято называть переходной характеристикой системы. Поскольку система стационарна, переходная характеристика инвариантна относительного временного сдвига:
.
Переход. х-ка физ-ки реал-мой системы отлична от нуля лишь при 
, в то время как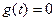 
при t <0.
Между имп. и перех. х-ками имеется тесная связь. Действительно, т.к. 
, то на основании (1)
.
Оператор диффер-ния d/dt и линейный оператор Т могут меняться местами, поэтому
или 
.
Еще одна форма ИД: 
.
|
|
|
