И анализ тела неопределенности. Сложный сигнал.

Вопросы выбора радиосигналов в РЛС. При оптимальной обработке радиосигналов на выходе приемника формируется сигнал, совпадающий по форме с автокорреляционной функцией. Поэтому возможность обнаружения, разрешения сигналов и оценки их параметров связаны с формой корреляционной функции.

Под разрешением сигналов с РЛ понимается возможность раздельно обнаруживать и измерять параметры сигналов от близкорасположенных целей. Решение этой задачи неизбежно осложняется действием шумов. Наибольший интерес в РЛ представляет разрешение сигналов по времени, несущей частоте и углу прихода сигнала. Сдвиг по времени несет информацию о дальности, сдвиг по частоте – о радиальной скорости, угловой сдвиг – об угловом положении цели. Количественно разрешающая способность по некоторому сигналу хар-ся разностью параметров двух разрешаемых сигналов, у к-рых остальные параметры одинаковы. , . Чтобы они мак-но разл-сь необходимо, чтобы наиб. зн-я имел ср. кв-т их разн-ти: . Интегрируя, получим: . Существенным для разрешения сигналов является изменение АКФ – .

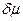Разрешение по углу определяется главным образом характеристиками системы, поэтому существенным для разрешения сигналов является выбор такого сигнала, у которого АКФ при временном и частотном сдвиге быстро убывает.

Двумерная КФ сигнала и анализ тела неопределенности. Сдвиг отраженного сигнала по времени связан с положением цели по дальности. Движение цели в радиальном направлении приводит к возникновению доплеровского сдвига несущей частоты сигнала на величину, пропорциональной радиальной скорости целей: , , где и – комплексные амплитуды двух гармонических сигналов и , которые различаются смещением по частоте . При этом условие (разрешающую способность) по и можно охарактеризовать интегралом: .

Этот интеграл называют двумерной КФ сигнала. Если , то эта функция вырождается в обычную АКФ. Если и , то (4). Эту функцию часто строят в корреляционном виде: 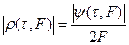– функция неопределенности зондирующего сигнала. Для частного случая график функции неопределенности представлен на рисунке. По рельефу этой функции можно судить о свойствах сигнала по его оптимальной обработке. Например, наличие острого основного максимума свидетельствует о возможности точного измерения дальности и скорости и высокой разрешающей способности сигнала. Для упрощения анализа тела неопределенности, сформированного графиком функции , иногда переходят к цилиндру, высота которого совпадает с максимумом функции неопределенности, а поперечное сечение совпадает с сечением тела неопределенности плоскостью, параллельной плоскости на уровне линии пересечения цилиндра и поверхности тела неопределенности, образующую на этом уровне эллипсоидальную фигуру, называемую диаграммой неопределенности (ДН) (заштрихованная часть на рисунке).

Сложный сигнал. Анализ тел неопределенности и ДН, выполненных при изучении РЛС, показывает, что при простых зондирующих сигналах (таких, у которых база или произведение длительности импульса на ширину его спектра равно 1). Вследствие постоянства объема функции неопределенности и площади ДН невозможно увеличивать одновременно разрешающую способность и точность по дальности и по скорости.

Требования одновременного возрастания точности по дальности и по скорости являются противоречивыми. Разрешения этого противоречия достигают применением так называемых сложных сигналов, у которых база . К таким сигналам относится ЛЧМ сигнал. У этого сигнала база может составлять сотни единиц. Коэффициент сжатия такого сигнала часто равен базе сигнала, что свидетельствует о соответствующем повышении максимума функции неопределенности и увеличении разрешающей способности. К числу сложных сигналов относят так называемые шумоподобные сигналы, у которых АКФ приближается по форме к -функции (не имеет боковых лепестков).

Хорошей разрешающей способностью обладают сигналы, синтезированные с использованием кодов Баркера, которые также имеют разновыраженный максимум АКФ и низкий уровень боковых лепестков.