 |
Интерактивный ввод матриц
|
|
|
|
Интерактивный ввод матриц
Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix:
> А:=аггау(1..3,1..3):
А:=аггау(1..3,1.. 3, [ ])
После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:
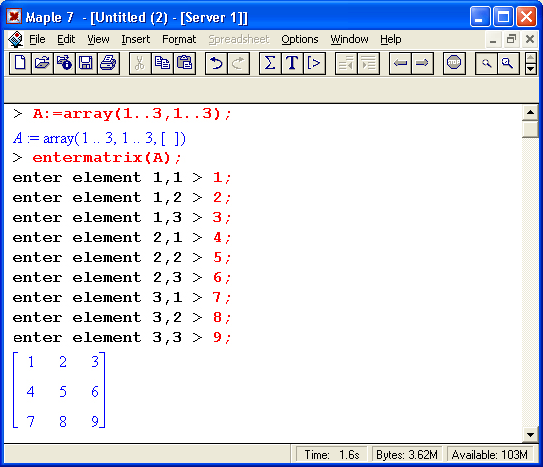
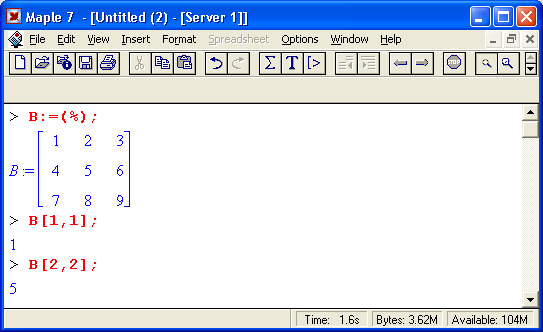
Gif

Gif

Основные функции для задания векторов и матриц
Основные функции для задания векторов и матриц
В библиотечном файле Unalg имеются следующие функции для задания векторов и матриц:
- vector(n,list) — сoздание вектора с n элементами, заданными в списке list;
- matrix(n,m,list) — создание матрицы с числом строк n и столбцов m с элементами, заданными списком list.
Ниже показано применение этих функций:
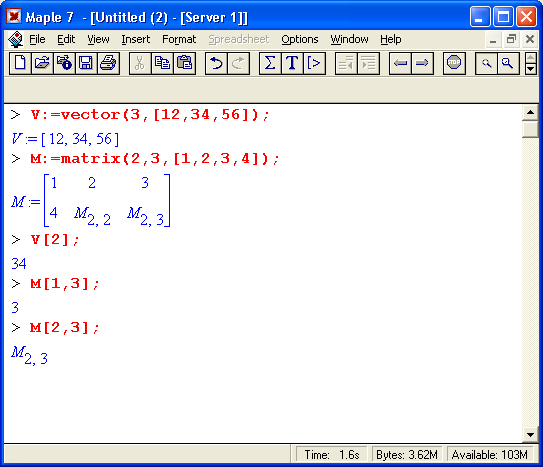
Обратите внимание на последние примеры — они показывают вызов индексированных переменных вектора и матрицы.
Gif

Функции для работы, с векторами и матрицами
Функции для работы с векторами и матрицами
Для работы с векторами и матрицами Maple 7 имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.
Операции со структурой отдельного вектора V и матрицы М:
- coldim(M) — возвращает число столбцов матрицы М;
- rowdim(M) — возвращает число строк матрицы М;
- vectdim(V) — возвращает размерность вектора V;
- col(M,i) — возвращает i-й столбец матрицы М;
- row(M,i) — возвращает i-ю строку матрицы М;
- tninor(M,i, j) — возвращает минор матрицы М для элемента с индексами i и j;
- delcols(M,i.. j) — удаляет столбцы матрицы М от i-roдо j-ro;
- del rows (V,i..j) — удаляет строки матрицы М от i-й до j-й;
- extend (М, т, n,х) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.
Основные векторные и матричные операции:
- dotprod(U,V) — возвращает скалярное произведение векторов U и V;
- crossprod(U,V) — возвращает векторное произведение векторов U и V;
- norm(V) или norm(M) — возвращает норму вектора или матрицы;
- copyinto(A,B,i, j) — копирует матрицу А в В для элементов последовательно от i до j;
- concat(Ml,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2;
- stack(Ml,M2) — возвращает объединенную матрицу с вертикальным слиянием Ml и М2;
- matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;
- multlply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;
- adjoint (М) или adj(M) — возвращает присоединенную матрицу, такую что M?adj(M) дает диагональную матрицу, определитель которой есть det(M);
- charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;
- det(M) — возвращает детерминант (определитель) матрицы М;
- Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;
- jordan(M) — возвращает матрицу М в форме Жордана;
- hermite(M) — возвращает матрицу М в эрмитовой форме;
- trace(M) — возвращает след матрицы М;
- rank(M) — возвращает ранг матрицы М;
- transpose(M) — возвращает транспонированную матрицу М;
- inverse(M) или evalm(l/M) — возвращает матрицу, обратную к М;
- singularvals(A) — возвращает сингулярные значения массива или матрицы А.
Приведем примеры применения некоторых из этих функций:
|
|
|
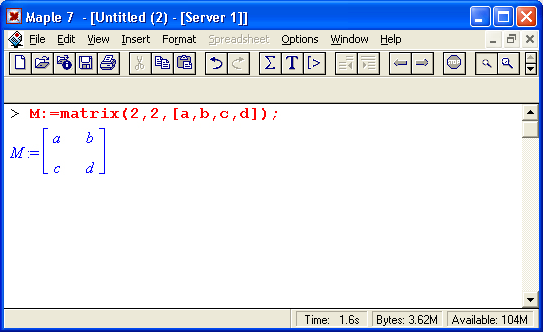
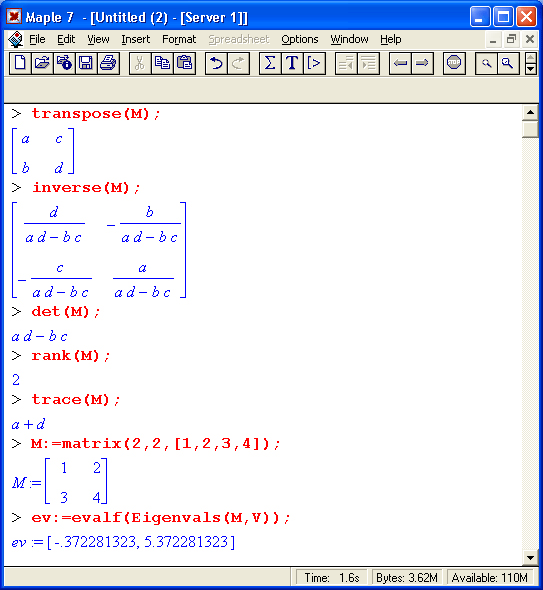
Читатель, понимающий суть матричных вычислений, легко справится с тестированием других функций, входящих в пакет linalg. В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.
Gif

Gif

|
|
|


