 |
Примеры применения пакета networks
|
|
|
|
Примеры применения пакета networks
Рассмотрим некоторые избранные функции этого пакета, которые наиболее часто используются при работе с графами. Детали синтаксиса функций можно найти в справочной базе данных Maple 7.
Функции создания графов:
- new — создает пустой граф (без ребер и узлов);
- void — создает пустой граф (без ребер);
- duplicate — создает копию графа;
- complete — создает полный граф;
- random — возвращает случайный граф;
- petersen — создает граф Петерсена. Функции модификации графов:
- addedges — добавляет в граф ребро;
- addvertex — добавляет в граф вершины;
- connect — соединяет одни заданные вершины с другими;
- delete — удаляет из графа ребро или вершину. Функции контроля структуры графов:
- draw — рисует граф;
- edges — возвращает список ребер графа;
- vertices — возвращает список узлов графа;
- show — возвращает таблицу с полной информацией о графе;.
- ends — возвращает имена вершин графа;
- head — возвращает имя вершины, которая является головой ребер;
- tail — возвращает ими вершины, которая является хвостом ребер;
- incidence — возвращает матрицу инцидентности;
- adjacency — возвращает матрицу смежности;
- eweight — возвращает веса ребер;
- weight — возвращает веса вершин;
- isplanar — упрощает граф, удаляя циклы и повторяющиеся ребра, и проверяет его на планарность (возвращает true, если граф оказался планарным, и false — в противном случае).
Функции с типовыми возможностями графов:
- flow — находит максимальный поток в сети от одной заданной вершины к другой;
- shortpathtree — находит кратчайший путь в графе с помощью алгоритма Дейкстры.
Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить с помощью справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.
|
|
|
На рис. 16.9 показан пример создания Графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.
На рис. 16.10 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.
В третьем примере (рис. 16.11) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину а с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.
В четвертом примере, представленном на рис.,16.12, показано создание графа G2 (его изображение было приведено на рис. 16.10) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и соmр — принимает значение множества, в котором содержатся вершины, по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.
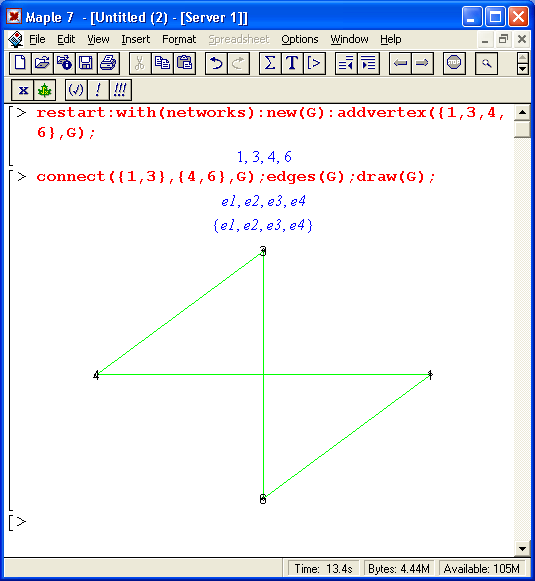
Рис. 16.9. Построение графов
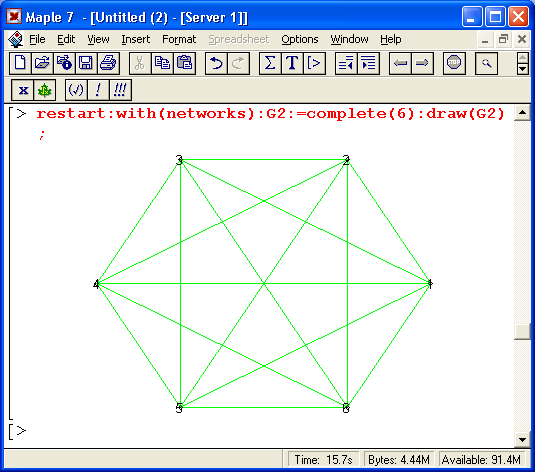
Рис. 16.10. Преобразование графа удалением части вершин
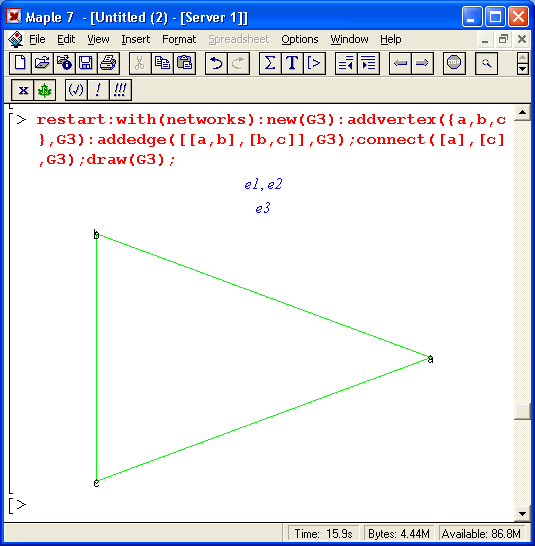
Рис. 16.11. Формирование графа и определение его «голов» и «хвостов»

Рис. 16.12. Пример вычисления максимального потока и наиболее коротких путей для заданного графа
Gif

Gif

Gif

Gif

|
|
|


