 |
Материальный баланс в сорбции
|
|
|
|
Закон сохранения вещества в применении к гетерофазной системе может быть сформулирован следующим образом:
сумма изменений в течение некоторого времени количества (массы) данного вещества по всем фазам равна разности вносимых в систему и выводимых из нее количеств этого вещества за то же время.
Исходя из этой формулировки, запишем уравнение материального баланса:
 (1)
(1)
где  - концентрация
- концентрация  -го вещества в
-го вещества в  –й фазе;
–й фазе;  - объем фазы;
- объем фазы;  - масса вещества, внесенного в систему;
- масса вещества, внесенного в систему; 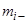 - масса вещества, выведенного из системы;
- масса вещества, выведенного из системы;  - границы временного интервала величиной
- границы временного интервала величиной  . Уравнение (1) справедливо для каждого вещества (компонента) рассматриваемой смеси. Если смесь содержит
. Уравнение (1) справедливо для каждого вещества (компонента) рассматриваемой смеси. Если смесь содержит  компонентов, то можно записать
компонентов, то можно записать  уравнений (1).
уравнений (1).
Для рассмотренного выше примера сорбции в статике уравнение (1) сильно упрощается:
 (2)
(2)
Здесь учтено, что система замкнута, т.е. правая часть уравнения (1) равна нулю; отсчет времени начинается после внесения смеси в систему, а равновесие, строго говоря, наступает в бесконечно удаленный момент времени.
Предположим, что первоначально в фазе сорбента (индекс «2») веществ, содержащихся в смеси, не было ( ); введем обозначения для фазового отношения:
); введем обозначения для фазового отношения:  , коэффициента распределения:
, коэффициента распределения:  , тогда получим удобную формулу для экспериментального нахождения коэффициента распределения (индекс первой фазы опущен):
, тогда получим удобную формулу для экспериментального нахождения коэффициента распределения (индекс первой фазы опущен):
 (3)
(3)
(справа приведено выражение с тривиальными обозначениями). Из формулы (3) следует, что для нахождения коэффициента распределения произвольного вещества в любой двухфазной системе методом сорбции в статике надо знать исходную концентрацию, конечную концентрацию и фазовое отношение.
Уравнение баланса для другого примера, приведенного выше, названного «кинетикой сорбции из ограниченного объема», отличается от уравнения (2) тем, что в его записи вместо равновесных концентраций  используются текущие величины
используются текущие величины  , зависящие от времени. При подстановке
, зависящие от времени. При подстановке  получим выражение искомой величины
получим выражение искомой величины  через измеряемую величину
через измеряемую величину  :
:
|
|
|
 , или в тривиальных обозначениях:
, или в тривиальных обозначениях:
 (4)
(4)
Далее перейдем к дифференциальным соотношениям, устремив к нулю интервал времени: 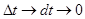 :
:
 (5)
(5)
где  - радиус-вектор точки на поверхности фазы,
- радиус-вектор точки на поверхности фазы,  - площадь поверхности фазы,
- площадь поверхности фазы,  - скорость вещества в данной фазе,
- скорость вещества в данной фазе,  - нормаль к поверхности в рассматриваемой точке, направленная во внешнюю сторону
- нормаль к поверхности в рассматриваемой точке, направленная во внешнюю сторону
Первое равенство в (5) получено из (1) с учетом того, что накопление вещества в фазе (отмечаемое знаком +) соответствует отрицательному знаку проекции скорости элемента вещества  на нормаль к поверхности и наоборот. Второе равенство является результатом применения теоремы Гаусса-Остроградского.
на нормаль к поверхности и наоборот. Второе равенство является результатом применения теоремы Гаусса-Остроградского.
Следующий шаг в получении дифференциального уравнения – уменьшение рассматриваемых пространственных областей ( ); тогда интеграл справа можно приближенно заменить произведением:
); тогда интеграл справа можно приближенно заменить произведением:
 (6)
(6)
В квадратных скобках уравнения (6) содержится хорошо известное выражение для непрерывного потока вещества, которое в отсутствие источников и поглотителей этого вещества должно быть равно нулю. Смысл уравнения (6) заключается, таким образом, в расширении условия непрерывности потока вещества на многофазную систему, в которой фазы могут служить друг для друга источниками и поглотителями вещества.
Предельное условие в (6) легко можно выполнить, рассматривая геометрическую систему с размерностью меньше 3. Наиболее важным и простым случаем является одномерная задача. К такому случаю сводится большинство динамических сорбционных процессов, использующих ламинарные режимы для подвижных фаз.
Из гидродинамики известно, что ламинарный поток может быть представлен в виде пучка одномерных трубок потока, не пересекающихся между собой. Поместив в такую трубку достаточно малые частицы неподвижной фазы, получим двухфазную систему, подчиняющуюся уравнению (6).
|
|
|
Сузим задачу выбором цилиндрической формы макросистемы. В сорбционных процессах эта система называется колонной, или колонкой. Продольная координата колонки совпадает с координатой вдоль трубки потока  . В цилиндрической трубке скорость подвижной фазы (фазы с индексом «1»)
. В цилиндрической трубке скорость подвижной фазы (фазы с индексом «1»)  и согласно (6) найдем:
и согласно (6) найдем:
 ,
,
где произведены подстановки:  - фазовое отношение,
- фазовое отношение,  - часть плотности потока вещества в подвижной фазе, которая не зависит от движения фазы, и
- часть плотности потока вещества в подвижной фазе, которая не зависит от движения фазы, и 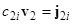 - вектор плотности потока в неподвижной фазе. Две последние величины определяются характером переноса вещества в неподвижной фазе (или в остановленной 1-й фазе): в отсутствие макроскопического движения перенос вещества осуществляется только посредством диффузии. Диффузионный поток пропорционален градиенту концентрации и направлен в противоположную сторону (1-й закон Фика):
- вектор плотности потока в неподвижной фазе. Две последние величины определяются характером переноса вещества в неподвижной фазе (или в остановленной 1-й фазе): в отсутствие макроскопического движения перенос вещества осуществляется только посредством диффузии. Диффузионный поток пропорционален градиенту концентрации и направлен в противоположную сторону (1-й закон Фика):
 ,
,
 (7)
(7)
где  - коэффициенты диффузии
- коэффициенты диффузии  -го компонента в фазах.
-го компонента в фазах.
Перегруппировав члены и имея в виду одномерность процесса, получим:
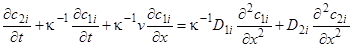 (8)
(8)
Уравнение (8) носит название условия материального баланса динамического сорбционного процесса. Правая часть включает в баланс так называемую продольную диффузию и придает всему дифференциальному уравнению в частных производных второй порядок. В тех случаях, когда его учет несуществен, порядок уравнения баланса понижается до первого.
В некоторых вариантах теории динамики сорбции, для удобства используют вместо фазового отношения понятие порозности, означающее долю объема системы, занимаемую подвижной фазой. При этом считается, что неподвижная фаза равномерно распределена по всему объему системы. То же полагается и для потока подвижной фазы: под живым сечением потока, т.е. сечением системы, проницаемым для подвижной фазы и перпендикулярным ее скорости, принимается полное сечение системы. Вводимая таким образом, нормировка параметров удобна при экспериментальной работе, однако она несколько смещает их физический смысл. Подстановка таких определений в (8) приводит к хорошо известному виду уравнения материального баланса:
|
|
|
 (9)
(9)
где  - порозность,
- порозность,  - так называемый коэффициент продольной диффузии – эффективная величина, слабо зависящая от координаты и времени как отношение вторых производных концентраций по координате, умноженное на малую, как правило, величину коэффициента внутренней диффузии. Более существенным фактором продольной дисперсии является гидродинамическая неоднородность, которая отражается в дополнительном слагаемом порядка произведения скорости ПФ на поперечный размер канала; в случае насадочной колонки этот размер сопоставим с диаметром зерен НФ (
- так называемый коэффициент продольной диффузии – эффективная величина, слабо зависящая от координаты и времени как отношение вторых производных концентраций по координате, умноженное на малую, как правило, величину коэффициента внутренней диффузии. Более существенным фактором продольной дисперсии является гидродинамическая неоднородность, которая отражается в дополнительном слагаемом порядка произведения скорости ПФ на поперечный размер канала; в случае насадочной колонки этот размер сопоставим с диаметром зерен НФ ( ). Оставив прежнее обозначение, для коэффициента продольной дисперсии запишем:
). Оставив прежнее обозначение, для коэффициента продольной дисперсии запишем:
 (10)
(10)
Наконец, в пренебрежении часто малым продольно-диффузионным членом из (9) получают уравнение первого порядка:
 (11)
(11)
Уравнение материального баланса (11) можно вывести более наглядно (рис.3.1).

Рис.3.1. Динамический баланс масс в элементе слоя сорбента длиной  и сечением s.
и сечением s.
Для величин закона сохранения масс в форме (1) получим (индекс i опущен):

где значок 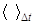 обозначает среднюю величину для малого интервала
обозначает среднюю величину для малого интервала  . Подставив полученные величины в (1) и устремив интервалы к нулю, получим (11).
. Подставив полученные величины в (1) и устремив интервалы к нулю, получим (11).
Цель применения уравнений типа (8-11) – найти закон перемещения зоны повышенного содержания данного вещества по сорбционной колонке. Известно, что в высокоэффективной хроматографии границы (фронты) такой зоны чрезвычайно резкие. Рассмотрим, как это отражается на величинах, входящих в уравнение (11). Наиболее быстрое перемещение вещества происходит в подвижной фазе, так что концентрация неподвижной фазы зависит от продольной координаты неявно – через концентрацию подвижной фазы:
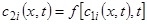 .
.
Запишем производные этой функции по времени и координате:
 , (12)
, (12)
где обозначены:  .
.
Резкий фронт вещества, переносимого по колонке, возникает только в том случае, когда зона вещества в подвижной фазе совпадает по скорости перемещения с ее образом в неподвижной фазе. Очевидно, что в противном случае зона вещества будет уширяться с течением времени тем сильнее, чем больше дисбаланс скоростей перемещения зоны в подвижной и неподвижной фазах. Скорость переноса вещества в какой-либо фазе определяется по скорости точки постоянной концентрации  , принадлежащей фронту вещества. Для подвижной фазы из условия постоянства концентрации получим:
, принадлежащей фронту вещества. Для подвижной фазы из условия постоянства концентрации получим:
|
|
|
 ,
,
откуда:
 (12а)
(12а)
Аналогично, для скорости соответствующей точки фронта вещества в неподвижной фазе имеем:
 (12б)
(12б)
Здесь обратим внимание на то, что производные в (12а) и (12б) соответствуют одной и той же точке на фронте. Таким образом, близость скоростей зависит от малости отношения  . Числитель этого отношения определяется кинетикой сорбции и тем меньше, чем быстрее она протекает. Знаменатель отношения есть производная концентрации сорбированного вещества по концентрации несорбированного вещества и при линейной изотерме сорбции равен коэффициенту распределения:
. Числитель этого отношения определяется кинетикой сорбции и тем меньше, чем быстрее она протекает. Знаменатель отношения есть производная концентрации сорбированного вещества по концентрации несорбированного вещества и при линейной изотерме сорбции равен коэффициенту распределения:
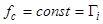 .
.
Если условие малости отношения  достигнуто (что является критерием высокой эффективности хроматографии), то для скорости фронта вещества из уравнения (11) получим:
достигнуто (что является критерием высокой эффективности хроматографии), то для скорости фронта вещества из уравнения (11) получим:
 ,
,
а в случае линейной изотермы (характерном для элютивной хроматографии):
 (13)
(13)
Воспользовавшись формулой (13), мы можем определить время, через которое зона вещества выйдет из колонки, разделив длину колонки  на скорость движения зоны:
на скорость движения зоны:
 (14)
(14)
Получили выражение для времени удерживания вещества ( ) в высокоэффективной хроматографии. Положив
) в высокоэффективной хроматографии. Положив  , найдем:
, найдем:  - время выхода неудерживаемого компонента, а так как оно совпадает с временем однократной смены подвижной фазы в колонке, его также называют «мертвым» временем и т.п.
- время выхода неудерживаемого компонента, а так как оно совпадает с временем однократной смены подвижной фазы в колонке, его также называют «мертвым» временем и т.п.
Определение времени удерживания по (14) сопряжено с ошибкой, связанной с отброшенным членом в (12б). В более точном приближении малый член  является поправкой к скорости фронта, и, следовательно, к времени удерживания:
является поправкой к скорости фронта, и, следовательно, к времени удерживания:  . Смысл неопределенности времени удерживания (
. Смысл неопределенности времени удерживания ( ) состоит в том, что хроматографический пик имеет соизмеримую ширину (
) состоит в том, что хроматографический пик имеет соизмеримую ширину ( ) и эта ширина обратно пропорциональна скорости процесса
) и эта ширина обратно пропорциональна скорости процесса  . Этот аспект является предметом кинетики сорбции, которая будет рассмотрена позже.
. Этот аспект является предметом кинетики сорбции, которая будет рассмотрена позже.
Связь (14) времени удерживания с коэффициентом распределения вещества составляет суть хроматографического метода. Различие в хроматографическом поведении компонентов пропорционально различию в их сорбируемости:
 (15)
(15)
Имеют место также и соотношения, явным образом не зависящие от параметров системы; они включают в себя только параметры выходной кривой процесса хроматографии – хроматограммы:
 (16)
(16)
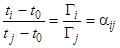 (17)
(17)
где  — коэффициент емкости для компонента – величина, аналогичная коэффициенту распределения,
— коэффициент емкости для компонента – величина, аналогичная коэффициенту распределения,  — коэффициент селективности разделения пары компонентов i и j.
— коэффициент селективности разделения пары компонентов i и j.
|
|
|
Чем сильнее коэффициент селективности отличается от 1, тем легче при прочих равных условиях провести хроматографическое разделение компонентов.
Сорбционное равновесие
Итак, термодинамическая природа аналита и хроматографической системы проявляется в коэффициенте распределения, который равен тангенсу угла наклона в начале зависимости концентрации компонента в неподвижной фазе от его концентрации в подвижной фазе при заданной температуре. Такая зависимость называется изотермой сорбции, она является основной характеристикой равновесия в сорбционной системе.
Условие равновесия фаз можно записать в виде уравнений химической реакции двух видов:
свободная сорбция -
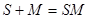 (18)
(18)
и конкурентная сорбция -
 , (19)
, (19)
где  - элемент неподвижной фазы (НФ), или сорбента, с которым взаимодействует 1 молекула аналита,
- элемент неподвижной фазы (НФ), или сорбента, с которым взаимодействует 1 молекула аналита,  - молекула аналита,
- молекула аналита,  - молекула подвижной фазы (ПФ),
- молекула подвижной фазы (ПФ),  - число (не обязательно целое) молекул подвижной фазы, вытесняемых из неподвижной фазы 1 молекулой аналита; назовем этот параметр показателем дискриминации молекул ПФ.
- число (не обязательно целое) молекул подвижной фазы, вытесняемых из неподвижной фазы 1 молекулой аналита; назовем этот параметр показателем дискриминации молекул ПФ.
При выводе условий материального баланса для элементов НФ, молекул ПФ и аналита надо иметь ввиду, что полные их концентрации равны соответственно:  . Для свободной сорбции запишем два уравнения:
. Для свободной сорбции запишем два уравнения:
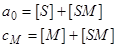 (20)
(20)
(как это принято в химических записях, квадратные скобки обозначают концентрацию вещества, символ которого указан в этих скобках). Для сорбции с конкуренцией запишем три балансовых уравнения:
 (21)
(21)
Случай свободной сорбции. Согласно закону действующих масс для свободной сорбции получим:
 ,
,
где второе равенство получено при подстановке  из (20). Отсюда следует выражение для концентрации аналита в НФ через его равновесную концентрацию в ПФ:
из (20). Отсюда следует выражение для концентрации аналита в НФ через его равновесную концентрацию в ПФ:
 (22)
(22)
Уравнение (22) называется уравнением изотермы Лэнгмюра (рис.3.2).

Рис.3.2. Вид изотермы Лэнгмюра. Пунктиром выделена область Генри.
Физический смысл параметров легко определить, исходя из предельных случаев: для  получим, что равновесная концентрация в НФ равна
получим, что равновесная концентрация в НФ равна 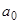 , т.е.
, т.е. 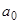 - предельная равновесная концентрация в НФ, или емкость сорбента (см. выше: определение емкости сорбента); для
- предельная равновесная концентрация в НФ, или емкость сорбента (см. выше: определение емкости сорбента); для  изотерма характеризуется линейным участком (так называемым участком Генри) с коэффициентом распределения, или константой Генри:
изотерма характеризуется линейным участком (так называемым участком Генри) с коэффициентом распределения, или константой Генри:
 (23)
(23)
Выражение (23) наглядно представляет структуру коэффициента распределения, о чем на качественном уровне говорилось выше: коэффициент распределения пропорционален сорбционной емкости и термодинамической константе (связанной экспоненциально с отношением энергии Гиббса к температуре и поэтому обусловливающей селективность сорбента к данному аналиту). Константа  является фактором селективности НФ по отношению к аналиту.
является фактором селективности НФ по отношению к аналиту.
Подстановка второго уравнения из (20) дает связь между общей и равновесной концентрацией аналита в ПФ, что актуально при рассмотрении замкнутых систем (см. выше: сорбция в статике).
Случай конкурентной сорбции. Аналогично, согласно закону действующих масс и первому из уравнений (21) для случая конкурентной сорбции получим:
 (24)
(24)
где приближение соответствует малой доле заполнения емкости сорбента аналитом. Выразим концентрацию аналита в НФ через его равновесную концентрацию в ПФ:
 (25)
(25)
Таким образом, случай конкурентной сорбции при любом показателе дискриминации  в первом приближении также описывается изотермой Лэнгмюра, а при
в первом приближении также описывается изотермой Лэнгмюра, а при 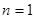 соотношение (25) выполняется в точности на всем интервале изменения концентрации аналита в ПФ.
соотношение (25) выполняется в точности на всем интервале изменения концентрации аналита в ПФ.
Из (25) для  найдем коэффициент распределения
найдем коэффициент распределения
 (26)
(26)
Выражение (26) указывает на то, что, в отличие от выражения (23) для случая свободной сорбции, при конкурентной сорбции коэффициент распределения обратно пропорционален концентрации молекул ПФ, взятой в степени показателя дискриминации.
Процессы, протекающие в различных видах хроматографии, имеют разный характер. Так, в газовой хроматографии реализуется свободная сорбция, а в жидкостной хроматографии – конкурентная сорбция.
Наиболее отчетливо характер конкурентной сорбции проявляется в ионном обмене и базирующихся на этом механизме хроматографических методах. Ионы взаимодействуют с ионообменником посредством кулоновских сил, приводя к локальной электронейтральности любого участка ионообменника. Благодаря этому гетерогенное равновесие записывается в форме ионного равновесия в гомогенном растворе:
 ,
,
где  - величины зарядов соответствующих ионов в единицах заряда электрона, знак зарядов, единый для всех ионов, участвующих в реакции, определяет тип ионного обмена: катионный или анионный (для примера взят обмен катионов); черта над символом указывает на форму, связанную с ионообменником.
- величины зарядов соответствующих ионов в единицах заряда электрона, знак зарядов, единый для всех ионов, участвующих в реакции, определяет тип ионного обмена: катионный или анионный (для примера взят обмен катионов); черта над символом указывает на форму, связанную с ионообменником.
Поделив все стехиометрические коэффициенты уравнения реакции на произведение зарядов, придем к записи, в которой у каждого члена только свои параметры:
 (27)
(27)
Сравнив (27) с (19), найдем показатель дискриминации ионов элюента (с индексом A): 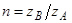 . Записав выражение для константы реакции, получим уравнение изотермы ионного обмена в форме уравнения Никольского:
. Записав выражение для константы реакции, получим уравнение изотермы ионного обмена в форме уравнения Никольского:
 (28)
(28)
Как было показано в общем случае конкурентной сорбции (см. выше: (25)), в первом приближении изотерма Никольского аппроксимируется изотермой Лэнгмюра. Связь между (24, 25) и (28) осуществляется путем замены:
 (29)
(29)
Используя эти переходы, найдем из (26) выражение для коэффициента распределения аналита в ионообменном процессе:
 (30)
(30)
Выше мы определяли емкость сорбента как предельную концентрацию аналита (в широком смысле — сорбата) в НФ. Такое определение ставит свойство сорбента – емкость – в зависимость от выбора сорбата.
· Локальная электронейтральность ионного обмена позволяет определить емкость как грамм-эквивалентную концентрацию функциональных групп, определенную на единицу объема или массы НФ – неизменяемое свойство ионообменника.
В этом случае в выражении (30) множитель 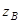 в скобке отсутствует.
в скобке отсутствует.
Выразим селективность сорбции через энергетические факторы. Из термодинамики химического равновесия известна связь константы равновесия реакции с изменением энергии Гиббса рассматриваемой системы:  . Изменение энергии Гиббса определяется изменениями энтальпии и энтропии:
. Изменение энергии Гиббса определяется изменениями энтальпии и энтропии:  . Энтальпия зависит от внутренней энергии системы, в которую входит не только тепловая энергия, но и энергия взаимодействия сорбата с сорбентом (имеющая характер притяжения, т.е. отрицательная по знаку). Энтропия существенно меняется только в реакциях с изменением числа частиц, например, в случае свободной сорбции. Таким образом, при прочих равных условиях сорбция тем сильнее, чем больше (по абсолютной величине) энергия притяжения между сорбатом и сорбентом.
. Энтальпия зависит от внутренней энергии системы, в которую входит не только тепловая энергия, но и энергия взаимодействия сорбата с сорбентом (имеющая характер притяжения, т.е. отрицательная по знаку). Энтропия существенно меняется только в реакциях с изменением числа частиц, например, в случае свободной сорбции. Таким образом, при прочих равных условиях сорбция тем сильнее, чем больше (по абсолютной величине) энергия притяжения между сорбатом и сорбентом.
Ввиду того, что условием сорбции является отрицательная величина разности энергий Гиббса, а не величина самой энергии Гиббса при равновесии, возможен другой механизм сорбции, основанный не на притяжении молекул к поверхности твердого тела, а на силе выталкивания молекул из жидкой фазы на границу раздела фаз. Для этого силы сцепления между молекулами жидкости должны быть намного больше обычных межмолекулярных сил дисперсионного и диполь-дипольного типа, характерных для взаимодействия молекул аналита с растворителем или с адсорбентом. Такими силами являются водородные связи, поэтому в качестве основного растворителя может рассматриваться вода, а механизм сорбции носит название «гидрофобного». Подчеркнем, что характеристики сорбции при гидрофобном механизме принципиально ничем не отличаются от характеристик физической адсорбции (с конкуренцией), основанной на силах притяжения к поверхности.
Итак, сорбционные процессы имеют сходные характеристики равновесия – изотермы, имеющие для небольших концентраций форму Лэнгмюра. В хроматографии рассматриваются настолько малые концентрации аналитов, что их распределение между фазами определяется начальным участком изотерм – областью Генри. Коэффициент распределения в этой области постоянен и в общем случае пропорционален емкости, константе равновесия сорбции и обратно пропорционален концентрации подвижной фазы в степени коэффициента дискриминации ее молекул.
Лекция 3 (2 часа)
Кинетика сорбции
Диффузионный, т.е. случайный, стохастический, характер движения молекул, очевидно, всегда приводит к уменьшению градиента концентрации, т.е. к размыванию фронта. Колонки в хроматографии используются достаточной длины, чтобы вероятность для молекулы аналита не побывать в неподвижной фазе была исчезающе мала. Таким образом, движение любой молекулы в колонке складывается из движения в ПФ и движения в НФ (рис.3.3). Неподвижная фаза в насадочных колонках в высокоэффективной хроматографии состоит из мелких гранул специального строения. Нижний предел по размеру зерен выбирают из гидродинамических соображений: слой сорбента в колонке должен быть достаточно проницаем для ПФ. Особенности строения гранулы должны обеспечивать максимально быстрый процесс сорбции – десорбции аналитов. В этой связи применяются сорбенты, имеющие слоистое строение, например, с тонким поверхностным слоем сорбирующего материала (или поверхностно-модифицированным слоем; см. «в» на рис. 3.3). Такие сорбенты называются пелликулярными, или поверхностно-слоистыми, или поверхностно-привитыми.
1. Движение молекулы в ПФ. В ПФ существует две области с различным характером движения молекул:
а - стремнинная область потока ПФ, где молекулы в среднем движутся со скоростью потока, их фронт здесь испытывает только продольно-диффузионное размытие, связанное с градиентом концентрации этого фронта;
б - приповерхностная область ПФ – область вблизи границы раздела фаз, где движение молекул определяется их диффузией через малоподвижную тонкую зону («пленку») вблизи сорбента. Впервые модель внешней диффузии как диффузии через пленку жидкости (модель пленочной диффузии) была предложена Нернстом, поэтому используется название «нернстовская пленка».
Подчеркнем, что в области а средняя скорость аналита равна скорости ПФ, а в области б равна нулю. В обеих областях имеет место диффузионное размытие фронта аналита: продольно-диффузионное – в области а и внешне-диффузионное, или пленочное, размытие – в области б. В местах контакта зерен (в области б’) толщина нернстовской пленки в несколько раз превышает среднюю величину; эти области характеризуются сильно замедленной внешнедиффузионной кинетикой и для поверхностно-слоистых сорбентов, чувствительных к поверхностным эффектам, фактически создают второй внешнедиффузионный процесс сорбции, протекающий параллельно с более быстрой диффузией в области б.
2. Движение молекулы в НФ. Диффузия молекулы внутри частиц НФ называется внутренней диффузией и определяется пористостью, геометрией пор сорбента, взаимодействием молекулы с его активными центрами, их плотностью. Все эти факторы отражаются на величине коэффициента диффузии, как правило, намного меньшей, чем коэффициент диффузии в ПФ. Время внутренней диффузии определяется также и средней длиной пути молекулы внутри НФ (в зоне в).
Выше уже говорилось (см. раздел 3.1), что разброс в положении фронтов одного и того же аналита в неподвижной и подвижной фазах связан с временем перехода молекул из ПФ в НФ (и наоборот). Указанный интервал времени q i складывается из интервалов, характерных для внешней q ai и внутренней диффузии q bi:
 (31)
(31)
В целом, кинетическое уравнение для высокоэффективного сорбционного процесса можно задать кинетическим уравнением химической реакции 1-го рода (ниже индекс компонента «i» опущен):
 (32)
(32)
Интересно было бы сравнить выражение (32) с (12): 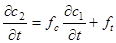 . Они тождественны при выполнении уравнений:
. Они тождественны при выполнении уравнений:
 (33)
(33)
где введенный параметр, согласно условию постоянства концентраций при равновесии, является равновесной концентрацией компонента в НФ:  .
.
Довольно сложные с экспериментальной точки зрения задачи кинетики упрощаются в тех случаях, когда один из двух последовательно протекающих процессов оказывается намного быстрее другого. Поэтому достаточно хорошо изученными являются частные случаи:
· 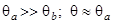 - внешнедиффузионная кинетика;
- внешнедиффузионная кинетика;
·  - внутридиффузионная кинетика.
- внутридиффузионная кинетика.
Уравнение внешнедиффузионной кинетики имеет вид:
 (34)
(34)
где 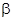 - внешнедиффузионный коэффициент, связанный со скоростью ПФ и диаметром зерен насадки соотношением:
- внешнедиффузионный коэффициент, связанный со скоростью ПФ и диаметром зерен насадки соотношением:  .
.
Уравнение внутридиффузионной кинетики имеет вид:
 (35)
(35)
где  - соответственно коэффициент внутренней диффузии, радиус зерна
- соответственно коэффициент внутренней диффузии, радиус зерна  сорбента или толщина сорбирующего слоя в зерне со слоистым строением.
сорбента или толщина сорбирующего слоя в зерне со слоистым строением.
Сравнивая (34,35) с (32), найдем:
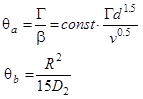 (35)
(35)
|
|
|


