 |
Первообразная и неопределенный интеграл
|
|
|
|
М.А. ЕВДОКИМОВ,
Л.В. ЛИМАНОВА
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
И ЕГО ПРИЛОЖЕНИЯ
Самара
Самарский государственный технический университет
2012
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
К а ф е д р а «Высшая математика и прикладная информатика»
М.А. ЕВДОКИМОВ,
Л.В. ЛИМАНОВА
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
И ЕГО ПРИЛОЖЕНИЯ
Утверждено редакционно-издательским советом университета
в качестве учебника
Самара
Самарский государственный технический университет
2012
УДК 517
Е 15
Рецензент д-р физ.-мат. наук, проф. Жданов А.И.
Евдокимов М.А.
Е15 Интегральное исчисление и его приложения: Учебник / М.А. Евдокимов, Л.В. Лиманова. – Самара: Самар. гос. техн. ун-т, 2012. – 209 с.
ISBN 978-5-7964-1155-1
При переходе к стандартам обучения по учебным планам бакалавриата неизбежно значительное сокращение учебных часов, отводимых на курс математики. Поэтому приходится изыскивать возможности внесения в программу разделов курса ранее изучавшихся отдельными главами, например, теории функции комплексного переменного. Так, в разделах «Введение в математический анализ» и «Дифференциальное исчисление» входят соответствующие темы из курса ТФКП. В данном учебном пособии авторы продолжили реализовывать эту концепцию построения курса высшей математики и ввели раздел, посвященный интегрированию функции комплексного переменного. Это соответствует принятой учебной программе бакалавриата для студентов многих инженерно-технических специальностей ВУЗов.
|
|
|
В каждый раздел включено достаточное количество задач, примеров и упражнений, многие из которых иллюстрируют связь математики с другими дисциплинами. Отличительной чертой данного учебного пособия является включение в него множества задач профессиональной направленности, подобранных для различных специальностей технического вуза.
Предназначен для студентов и преподавателей технических университетов.
УДК 517
Е 15
ISBN 978-5-7964-1155-1 © М.А. Евдокимов, Л.В. Лиманова,
2012
© Самарский государственный
технический университет, 2012
ВВЕДЕНИЕ
Понятие «интеграл» непосредственно связано с интегральным исчислением − разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления. Вместе с дифференциальным исчислением интегральное исчисление составляет основу математического анализа.
Истоки интегрального исчисления относятся к античному периоду развития математики и берут начало от метода исчерпывания, разработанного математиками Древней Греции. Метод исчерпывания − это набор правил для вычисления площадей и объёмов, разработка которых приписывается Евдоксу Книдскому[1]. Дальнейшее развитие метод получил в работах Евклида, а особым искусством и разнообразием применения метода исчерпывания славился Архимед.
Упадок древнего мира привёл к забвению многих научных достижений. О методе исчерпывания вспомнили лишь в XVII веке. Это было связано с именами Исаака Ньютона, Готфрида Лейбница, Леонарда Эйлера и ряда других выдающихся учёных, заложивших основу современного математического анализа. В конце XVII и в XVIII веке все возрастающие запросы практики и других наук побуждали ученых-математиков максимально расширять область приложения математических методов.
В конце XVII и в XVIII веке в математике и механике были получены классические результаты фундаментального значения. Основным здесь было развитие дифференциального и интегрального исчисления, теории дифференциальных уравнений, вариационного исчисления и аналитической механики.
|
|
|
Основные понятия и теория интегрального и дифференциального исчислений, прежде всего связь операций дифференцирования и интегрирования, а также их применения к решению прикладных задач были разработаны в конце XVII века, но основывались на идеях, сформулированных в начале XVII веке великим математиком и астрономом Иоганом Кеплером. Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование − взаимно обратные операции.
Примерно с последней четверти XVIII века область приложений математического анализа начинает значительно перекрывать границы его обычного приложения в механике и геометрии. Ещё быстрее развертывается этот процесс в первой четверти XIX века.
Дух времени требовал аналитического пути развития точных наук, применения дифференциального и интегрального исчисления для описания физических явлений. Этот путь и начал прокладывать Леонард Эйлер.
Это было время, когда великие идеи Ньютона и Лейбница были опубликованы сравнительно недавно, и современный математический анализ только создавался. Мощные методы, которые принесли с собой эти идеи, находили применение во всех отраслях точного знания. Применение это шло рука об руку с развитием самого анализа, часто указывая пути и направления, по которым должно развиваться новое исчисление. Это была, пожалуй, единственная по своей интенсивности эпоха математического творчества, и Эйлер был одним из немногих по своей продуктивности творцов. Его «Введение в анализ бесконечно малых», «Основания дифференциального исчисления» и «Основания интегрального исчисления» были первыми трактатами, в которых уже обширный, но разрозненный материал нового анализа был объединен в цельную науку. В них был выработан тот скелет современного анализа, который сохранился и до нашего времени.
|
|
|
В развитии интегрального исчисления приняли участие русские математики М.В. Остроградский (1801-1862), В.Я. Буняковский (1804-1889), П.Л. Чебышев (1821-1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, невыразимые через элементарные функции. Строгое изложение теории интеграла появилось только в XIX веке. Решение этой задачи связано с именами О. Коши (1789-1857), немецкого ученого Б. Римана (1826-1866), французского математика Г. Дарбу (1842-1917). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1826-1922) теории меры. Эти работы стали теоретическим обоснованием построения интеграла по мере и развития теории кратных, криволинейных интегралов, а также интегралов теории функции комплексного переменного. Различные обобщения понятия интеграла уже в начале двадцатого столетия были предложены французскими математиками А. Лебегом (1875-1941) и А. Данжуа (1884-1974), советским математиком А.Я. Хичиным (1894-1959).
Сегодня понятия производной и интеграла стали необходимыми элементами общей культуры человека. Они расширяют кругозор и оказываются полезными не только при решении технических задач, но и в самых разных областях знаний.
1. неопределенный интеграл
Первообразная и неопределенный интеграл
Пусть дана функция  Тогда производная
Тогда производная  Оператор, сопоставляющий функции её производную, называется оператором дифференцирования D:
Оператор, сопоставляющий функции её производную, называется оператором дифференцирования D:

Рассмотрим обратную задачу: зная функцию  найти функцию
найти функцию  , производная которой равна
, производная которой равна 
 (1.1)
(1.1)
Говорят, что функция F (x)является первообразной для функции f (x).
Примеры
1) 
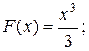
2) первообразной для функции  является функция
является функция  Вместе с тем первообразной будет и функция
Вместе с тем первообразной будет и функция  , и
, и  , и т. д.
, и т. д.
Из последнего примера следует, что задача об отыскании первообразной не имеет единственного решения.
Теорема 1 (о виде первообразных). Любые две первообразные для одной и той же функции различаются лишь на постоянную величину.
Доказательство. Пусть F (x) и Ф(х) – две первообразные для функции f (x), т. е.
|
|
|

Таким образом, любая первообразная для заданной функции имеет вид
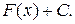
Здесь F (x) – какая-либо первообразная; С – произвольная постоянная.
Совокупность всех первообразных для функции f (x)называется неопределённым интегралом от функции f (x) и обозначается

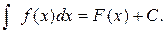 (1.2)
(1.2)
В (1.2) f (x)называется подынтегральной функцией, f (x) dx – подынтегральным выражением. Процедура вычисления неопределённого интеграла называется интегрированием функции f (x).
Геометрический смысл неопределённого интеграла ясен из рис. 1.1, где показано множество кривых, каждая из которых может быть получена сдвигом кривой y = F (x)в направлении оси ординат. Неопределённый интеграл есть произвольный элемент y = F (x) + С указанного семейства кривых.
На неопределённый интеграл можно смотреть как на оператор, действующий из С в С 1:

Оператор интегрирования иногда обозначают следующим образом:

имея в виду, что если заменить точку функцией f (x), то получится значение оператора на функции f (x).
Теорема 2 (о существовании неопределённого интеграла). Для всякой функции класса С [ a , b ] существует неопределённый интеграл на том же отрезке  .
.
В данном курсе доказательство этой теоремы не рассматривается.
1.2. Основные свойства неопределённого интеграла
1. Производная от неопределённого интеграла равна подынтегральной функции:
 (1.3)
(1.3)
Доказательство:
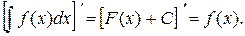
2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

Доказательство:
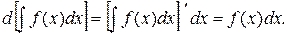
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

Доказательство:

4. Постоянный множитель можно выносить за знак неопределённого интеграла:
 (1.4)
(1.4)
Доказательство. Знак равенства в (1.4) понимается как совпадение производных для левой и правой частей. Отсюда следует очень простое доказательство

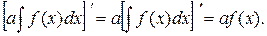
5. Неопределённый интеграл от суммы функций равен сумме интегралов от этих функций, если интегралы существуют:
 (1.5)
(1.5)
Доказательство. Доказательство проводится аналогично доказательству свойства 4:
 ,
,
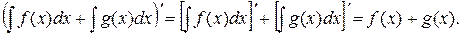
Из равенств (1.4), (1.5) следует, что оператор интегрирования является линейным оператором, что аналитически можно записать так
 .
.
1.3. Таблица основных интегралов
Приведём основные формулы для интегрирования элементарных функций. Часть этих формул известна из школьного курса математики.
1. 
2. 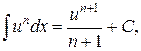

частный случай 

3. 
4. 

5. 
6. 
7. 
8. 
9. 
10. 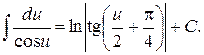
11. 
12. 
13. 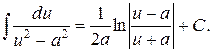
14. 
15. 
16. 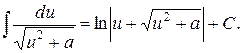
Приведенные формулы проверяют с помощью дифференцирования. Например, проверим формулу 15:
|
|
|

Аналогично убеждаемся в справедливости формулы 3:
 .
.
В качестве упражнения докажите справедливость формул 13, 14, 16.
Примеры. Вычислить интегралы:
1. 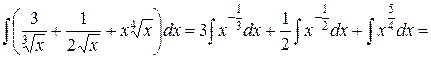
 .
.
2. 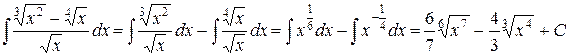 .
.
3. 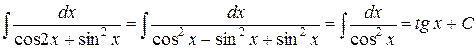 .
.
4. 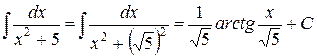 .
.
5. 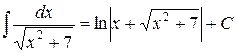 .
.
6.  .
.
7.  .
.
8. 
 .
.
|
|
|


