 |
Тригонометрические подстановки
|
|
|
|
Интегралы вида  ,
, 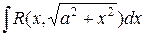 ,
, 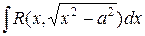 приводятся к рациональной функции относительно
приводятся к рациональной функции относительно  и
и  с помощью тригонометрических подстановок:
с помощью тригонометрических подстановок:
 -
- 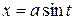 или
или 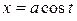 ;
;
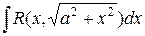 -
-  или
или 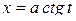 ;
;
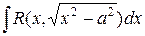 -
- 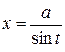 или
или 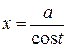 .
.
Получившиеся рациональные тригонометрические функции интегрируются разобранными выше методами.
Пример 1. Найти интеграл
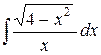 .
.
Решение
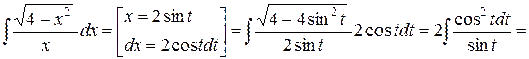
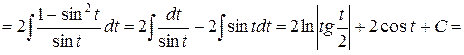
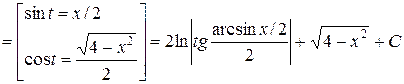 .
.
Пример 2. Найти интеграл
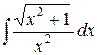 .
.
Решение
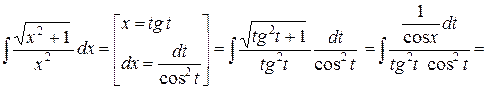
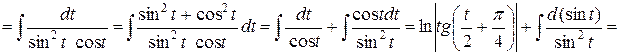
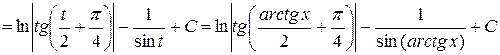 .
.
Пример 3. Найти интеграл
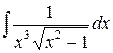 .
.
Решение
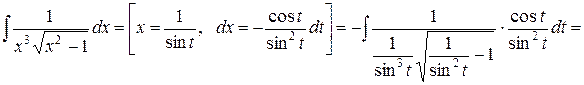


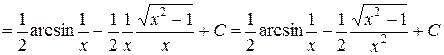 .
.
6. Интегралы вида 
Интеграл данного вида может быть преобразован к интегралу вида 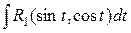 , который был рассмотрен в п. 1.9.5.
, который был рассмотрен в п. 1.9.5.
Произведем преобразования трехчлена, стоящего под корнем:
 .
.
Сделаем замену переменной, положив 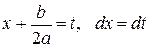 . Тогда
. Тогда
 .
.
Рассмотрим все возможные случаи.
1. Пусть  ,
, 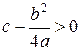 . Введем обозначения
. Введем обозначения 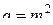 ,
,  . В этом случае будем иметь
. В этом случае будем иметь
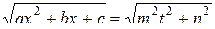 .
.
2. Пусть  ,
, 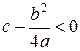 . Тогда
. Тогда 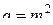 ,
, 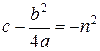 . Следовательно,
. Следовательно,
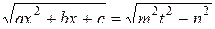 .
.
3. Пусть  ,
, 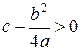 . Тогда
. Тогда  ,
, 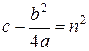 . Следовательно,
. Следовательно,
 .
.
4. Пусть  ,
, 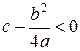 . В этом случае
. В этом случае 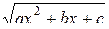 есть комплексное число при любом x.
есть комплексное число при любом x.
Таким образом, данный интеграл преобразуется к одному из следующих типов интегралов:
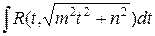 ,
, 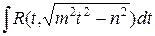 ,
, 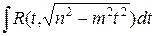 ,
,
которые сводятся к интегралам, рассмотренным в п. 1.9.5.
Пример. Вычислить интеграл
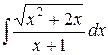 .
.
Решение
Преобразуем подкоренное выражение, выделив полный квадрат:
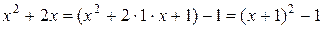 ,
,
т. е.  ,
, 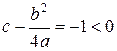 , получили второй случай. Значит,
, получили второй случай. Значит,
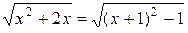 .
.
Выражение соответствует третьему случаю тригонометрических подстановок (см. п. 1.9.5). Выполним замену: 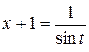 ,
, 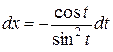 .
.
Подставляя полученные выражения в исходный интеграл, находим
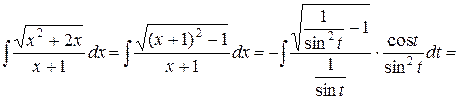
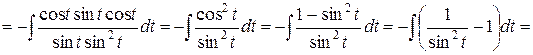
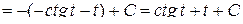 .
.
Возвращаясь к старой переменной с помощью формул
 и
и 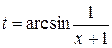 ,
,
получим
 .
.
Задания для самостоятельного решения
Вычислить интегралы:
1. 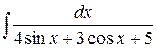 . Ответ.
. Ответ. 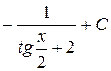 .
.
2.  . Ответ.
. Ответ. 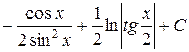 .
.
3. 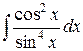 . Ответ.
. Ответ.  .
.
4. 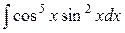 . Ответ.
. Ответ. 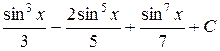 .
.
5. 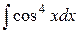 . Ответ.
. Ответ. 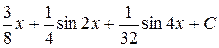 .
.
|
|
|
6.  . Ответ.
. Ответ. 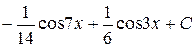 .
.
7. 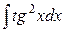 . Ответ.
. Ответ. 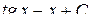 .
.
8.  . Ответ.
. Ответ.  .
.
9.  . Ответ.
. Ответ.  .
.
10. 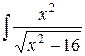 . Ответ.
. Ответ.  .
.
11.  . Ответ.
. Ответ. 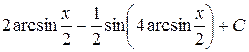 .
.
1.10. Функции, интегралы от которых
не выражаются через элементарные функции
В п. 1.1 отмечалось, что всякая функция f (x), непрерывная на интервале (a, b), имеет на этом интервале первообразную, т. е. существует такая функция F (x), что 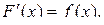 Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами
Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами 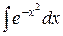 ,
, 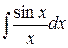 ,
,  ,
,  ,
,  , и многие другие.
, и многие другие.
Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций. Так, например, та из первообразных  , которая обращается в нуль при x = 0, называется функцией Лапласа и обозначается Ф(х). Таким образом,
, которая обращается в нуль при x = 0, называется функцией Лапласа и обозначается Ф(х). Таким образом,
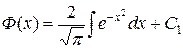 , если Ф (0) = 0.
, если Ф (0) = 0.
Эта функция хорошо изучена. Составлены подробные таблицы ее значений при различных значениях х [12].
Та из первообразных 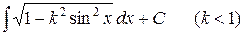 , которая обращается в нуль при x = 0, называется эллиптическим интегралом и обозначается Е(х), т. е.
, которая обращается в нуль при x = 0, называется эллиптическим интегралом и обозначается Е(х), т. е.
 , если Е (0) = 0.
, если Е (0) = 0.
Для этой функции также составлены таблицы значений при различных значениях х.
Такие функции называются специальными и получили широкое применение в различных приложениях. Методы их вычисления и свойства будут рассмотрены в соответствующих разделах курса математики.
Контрольные вопросы
по теме «Неопределенный интеграл»
1. Является ли оператор интегрирования линейным оператором? Какие из свойств это доказывают?
2. В качестве упражнения докажите справедливость формул
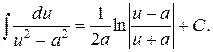

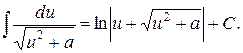
3. Доказать свойство
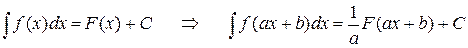 .
.
4. Почему не пишется произвольная постоянная в правой части равенства (формула по частям)
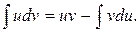
5. Какую функцию выбрать в качестве u (x)в интегралах
|
|
|
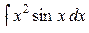 ,
, 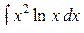 ,
, 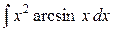 ,
,
вычисляемых по частям.
6. Как разложить правильную рациональную дробь на простейшие дроби?
7. Как выделить целую часть неправильной рациональной дроби? (группировка, деление многочленов)
8. Что такое «универсальная тригонометрическая подстановка»?
2. Интеграл по мере области
2.1. Понятие интеграла по мере области
При решении многих задач физики, техники, математики требуется вычислить какие-то суммарные характеристики рассматриваемого объекта или процесса (часто говорят: «интегральные характеристики»). При этом характеристики объекта или процесса могут быть переменными: говорят, что локальные характеристики переменны и зависят от координат, времени. К таким задачам относятся, например, задачи отыскания площади, объема тел различной конфигурации, массы, моментов инерции тел, материал которых имеет различную плотность в различных точках, нахождения пути, пройденного материальной точкой при движении с изменяющейся скоростью, и т. д.
При решении таких задач используется общая математическая модель – интеграл по мере (или «интеграл по фигуре»).
Рассмотрим, как решается задача об отыскании массы тела, плотность которого в каждой точке известна и различна. Этим телом (фигурой) может быть:
1) прямолинейный стержень – l;
2) криволинейный стержень – L;
3) плоская пластина любой формы – D;
4) криволинейная поверхность – G;
5) тело, ограниченное любыми поверхностями, – V.
Чтобы обобщить эти объекты, будем говорить о фигуре G, обладающей некоторой массой. Пусть известна плотность распределения массы этой фигуры в каждой её точке Р
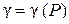 .
.
Так как масса – величина положительная, то необходимо считать эту функцию непрерывной и положительной на G.
Вычислим массу такой фигуры.
1. Разобьем фигуру G произвольным образом на непересекающиеся части  . Заметим, что при таком делении мы используем метрическую характеристику:
. Заметим, что при таком делении мы используем метрическую характеристику:
- в  – длина;
– длина;
- в 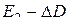 – площадь;
– площадь;
- в 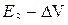 – объем.
– объем.
Будем обозначать эту характеристику 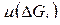 и назовём её мерой.
и назовём её мерой.
Меру можно представить как функцию множества
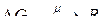 ,
,
т. е. множество 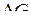 отображается на множество действительных чисел.
отображается на множество действительных чисел.
Основные свойства меры:
а) неотрицательность
 ;
;
б) аддитивность
 ,
,
предполагается, что 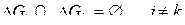 .
.
|
|
|
2. В каждой части выберем произвольную точку Pi и предположим, что плотность массы постоянна в пределах 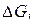 и равна её значению в точке Pi, т. е.
и равна её значению в точке Pi, т. е.  .
.
3. Определим приближенное значение массы части 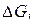
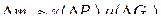 .
.
4. Масса (приближение) всей фигуры ищется суммированием частичных масс 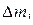
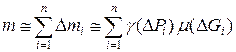 .
.
Выражение, стоящее справа, называется интегральной суммой.
5. Для нахождения точного значения массы переходим к пределу, устремив к нулю наибольший из диаметров частей  . Обозначим его
. Обозначим его 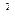 :
:
 .
.
Тогда
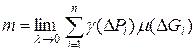 .
.
Заметим, что при 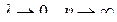 .
.
Если теперь отвлечься от конкретной задачи поиска массы, то можно составить интегральную сумму для некоторой непрерывной функции f (P), заданной на замкнутой, ограниченной фигуре G (можно говорить о замкнутой, ограниченной области, множестве). Это выражение вида
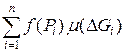 .
.
Рассмотрим предел этих интегральных сумм при  Если этот предел не зависит ни от способа разбиения фигуры на части
Если этот предел не зависит ни от способа разбиения фигуры на части  , ни от выбора точек Pi в каждой из частей, то его называют интегралом по мере (по фигуре)
, ни от выбора точек Pi в каждой из частей, то его называют интегралом по мере (по фигуре) 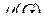 от функции f (P) и обозначают
от функции f (P) и обозначают
 . (2.1)
. (2.1)
 Конкретизируем введенные понятия для различных фигур.
Конкретизируем введенные понятия для различных фигур.
I. Для отрезка [ a, b ] оси 0х (отрезок прямолинейного стержня, рис. 2.1)
 (2.2)
(2.2)
− это обычный определенный интеграл.
Если  − линейная плотность материала стержня, то (2.2) выражает его массу.
− линейная плотность материала стержня, то (2.2) выражает его массу.
II. Для пространственной кривой l (рис. 2.2), т. е. G – это часть кривой, интеграл (2.1) принимает вид
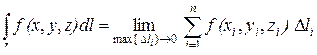 . (2.3)
. (2.3)
 Если
Если 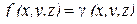 – функция линейной плотности массы, то (2.3) определяет массу криволинейного стержня.
– функция линейной плотности массы, то (2.3) определяет массу криволинейного стержня.
Для плоской кривой выражение (2.3) немного упрощается:
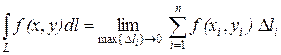 . (2.4)
. (2.4)
Интегралы (2.3) и (2.4) называются криволинейными интегралами по длине дуги, или криволинейными интегралами I рода.
III. В пространстве R 2 в качестве фигуры имеем ограниченную часть плоскости – область D (рис. 2.3). Тогда

 ,
,  .
.
Интеграл (2.1) принимает вид
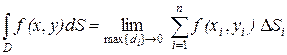 , (2.5)
, (2.5)
где di – диаметр 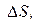 .
.
Интеграл (2.5) называется двойным интегралом по области D.
Если 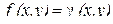 – функция плотности массы, то (2.5) выражает массу неоднородной пластины.
– функция плотности массы, то (2.5) выражает массу неоднородной пластины.
IV. Для поверхности Q, где
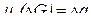 ,
, 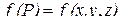 ,
,
интеграл (2.1) принимает вид
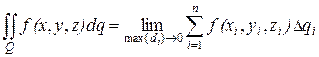 (2.6)
(2.6)
|
|
|
и называется поверхностным интегралом по площади поверхности.
Если 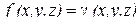 – функция поверхностной плотности массы, то (2.6) выражает массу поверхности Q.
– функция поверхностной плотности массы, то (2.6) выражает массу поверхности Q.
 V. Для пространственного тела Т (рис. 2.4), где
V. Для пространственного тела Т (рис. 2.4), где
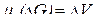 ,
, 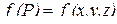 ,
,
интеграл (2.1) принимает вид
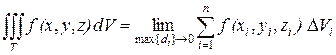 (2.7)
(2.7)
и называется тройным интегралом по области Т.
Если 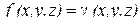 − функция объемной плотности массы, то (2.7) выражает массу тела Т.
− функция объемной плотности массы, то (2.7) выражает массу тела Т.
2.2. Основные свойства интеграла по мере области
1. Аддитивность относительно подынтегральной функции
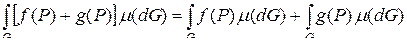
(при этом каждый интеграл должен существовать).
Для доказательства достаточно учесть, что
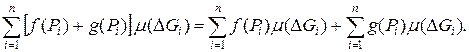
2. Однородность
 , С = const.
, С = const.
Это свойство следует из очевидного равенства
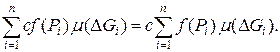
Объединяя свойства 1 и 2, можно сказать, что интеграл по мере области является линейным функционалом.
3. Если f (P)  1, то
1, то 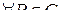
 .
.
Доказательство следует из определения интеграла по мере (формула (2.1)).
Конкретизируем это важное свойство:
· 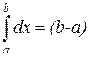 – длина отрезка
– длина отрезка 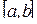 ;
;
·  – длина линии L;
– длина линии L;
· 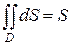 – площадь области D;
– площадь области D;
·  – площадь поверхности Q;
– площадь поверхности Q;
· 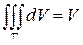 – объём тела Т.
– объём тела Т.
4. Если  , то
, то
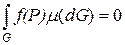 .
.
Например:
1) двойной интеграл по области G, которая является дугой кривой;
2) определенный интеграл, когда областью является точка, т. е. отрезок 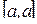 .
.
5. Аддитивность относительно области интегрирования
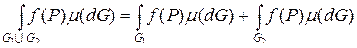 , если
, если 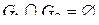 .
.
Доказательство
Рассмотрим область в пространстве R 2. Тогда
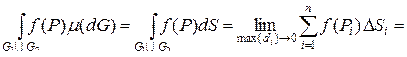

 .
.
6. Теорема о знаке интеграла по мере.
Если  .
.
Доказательство следует из определения интеграла по мере (формула (2.1)).
7. Если 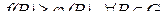 , то
, то
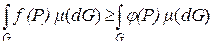 .
.
Доказательство
Так как 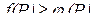 , то
, то 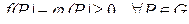 . Проинтегрируем обе части этого неравенства по области G:
. Проинтегрируем обе части этого неравенства по области G:
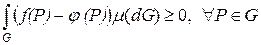 .
.
Тогда

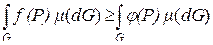 .
.
Из этого свойства следует, что неравенства можно почленно интегрировать.
8. Если 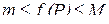 , то
, то
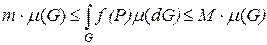 .
.
Доказательство следует из свойств 3 и 7.
Это свойство определяет двустороннюю оценку интеграла по мере.
Пример 1. Рассмотрим определенный интеграл.
 Сравним площади фигур
Сравним площади фигур  ,
,  ,
, 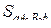 . Из рис. 2.5 очевидно, что
. Из рис. 2.5 очевидно, что
 .
.
Вычислив площади прямоугольников, получим
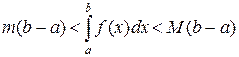 .
.
9. Оценка модуля интеграла по мере области
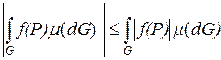 .
.
Доказательство
По определению интеграла по мере имеем
 .
.
Воспользуемся свойством модуля  , тогда
, тогда
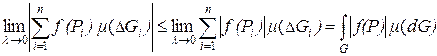 .
.
Таким образом, получаем
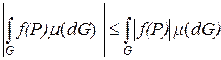 .
.
10. Теорема о среднем значении функции в области с ненулевой мерой. Если функция f (P) непрерывна на замкнутой ограниченной фигуре G, то найдется такая точка 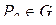 , что
, что
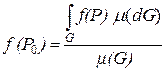 .
.
Доказательство
Так как фигура G ограничена и функция f (P) непрерывна, то функция f (P) принимает на G свои наибольшее  и наименьшее
и наименьшее 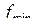 значения, т. е.
значения, т. е.
 .
.
Проинтегрируем это неравенство
 .
.
Воспользуемся свойством 8
 .
.
Разделим неравенство на  :
:
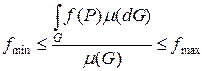 ,
,
т. е. величина 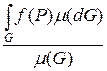 заключена между
заключена между 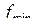 и
и 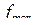 . Функция f(P) непрерывна и принимает значения между
. Функция f(P) непрерывна и принимает значения между 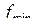 и
и 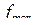 . Значит, она должна принять и это значение в некоторой точке P0. Таким образом,
. Значит, она должна принять и это значение в некоторой точке P0. Таким образом,
|
|
|
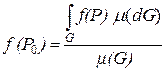 .
.
Пример 2. Рассмотрим определенный интеграл.
 На отрезке
На отрезке 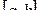 найдется точка
найдется точка 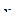 такая, что площадь криволинейной трапеции аАВ b будет равна площади прямоугольника аА1В1 b (рис. 2.6):
такая, что площадь криволинейной трапеции аАВ b будет равна площади прямоугольника аА1В1 b (рис. 2.6):
 .
.
Отсюда
 .
.
2.3. Вычисление определенного интеграла
2.3.1. Формула Ньютона − Лейбница
Пусть 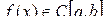 . Как было показано ранее, определенным интегралом от функции f (x) по отрезку
. Как было показано ранее, определенным интегралом от функции f (x) по отрезку 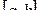 называется
называется
 , (2.8)
, (2.8)
причем а называется нижним пределом интегрирования, b – верхним пределом интегрирования.
Если 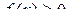 то величину определенного интеграла естественно принять за площадь криволинейной трапеции
то величину определенного интеграла естественно принять за площадь криволинейной трапеции  (рис. 2.7).
(рис. 2.7).
Формула, найденная Ньютоном и Лейбницем (независимо друг от друга), устанавливает связь между определённым и неопределённым интегралами. Она позволяет эффективно вычислять определенные интегралы и является основной формулой интегрального исчисления.
 Разобьем отрезок
Разобьем отрезок  на n частей (не обязательно равных по длине). Абсциссы границ полученных частей обозначим через
на n частей (не обязательно равных по длине). Абсциссы границ полученных частей обозначим через 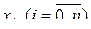 :
:
 .
.
Очевидно, справедливо равенство
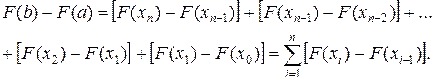 (2.9)
(2.9)
Пусть  Тогда по теореме Лагранжа
Тогда по теореме Лагранжа
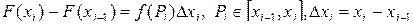
и формуле (2.9) можно придать вид
 (2.10)
(2.10)
Формула (2.10) показывает, что при соответствующем выборе точек 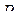 величина интегральной суммы при любом n постоянна и равна
величина интегральной суммы при любом n постоянна и равна  Поэтому при
Поэтому при 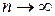 получим формулу
получим формулу
 ,
,
которую называют формулой Ньютона − Лейбница.
Определённый интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.
Для обозначения приращения функции 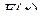 на отрезке
на отрезке  часто используют знак двойной подстановки
часто используют знак двойной подстановки
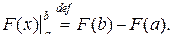
Формулу Ньютона − Лейбница можно вывести и другим способом.
Рассмотрим определённый интеграл
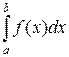 .
.
Для его существования необходимо, чтобы функция 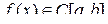 . Очевидно, что интеграл зависит от пределов интегрирования а и b.
. Очевидно, что интеграл зависит от пределов интегрирования а и b.
Если закрепить а, а верхнюю границу сделать переменной, то интеграл
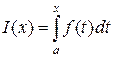
будет представлять некоторую функцию от х. Вычислим производную этой функции по переменной х. Для этого найдем
 .
.
Тогда
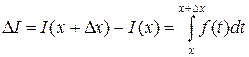 .
.
Применим теорему о среднем
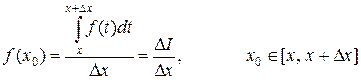 .
.
Перейдем к пределу при 
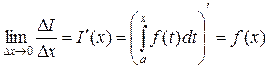 ,
,
так как 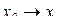 при
при 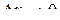 .
.
Итак, мы доказали теорему Барроу.
Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу равна подынтегральной функции, вычисленной на верхнем пределе.
Эта теорема является одной из основных теорем математического анализа и вскрывает глубокую связь между операциями определенного интегрирования и дифференцирования.
Следствие. Любая функция f (x), непрерывная на  , имеет первообразную, выражаемую формулой
, имеет первообразную, выражаемую формулой
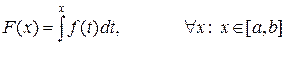 .
.
Исходя из геометрического смысла определённого интеграла как площади криволинейной трапеции, заметим, что соотношение
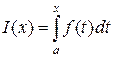
выражает переменную площадь криволинейной трапеции с основанием 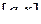 .
.
Теорема Барроу позволяет установить простой метод вычисления определённого интеграла.
Мы установили, что 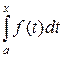 является первообразной для f (x). Первообразная имеет вид
является первообразной для f (x). Первообразная имеет вид
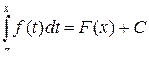 .
.
Пусть х = а, тогда
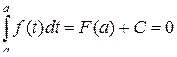 .
.
Тогда  . Подставим значение С в определение первообразной
. Подставим значение С в определение первообразной
 .
.
Пусть теперь х = b, тогда
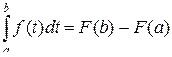 .
.
Получили формулу Ньютона – Лейбница, которая устанавливает связь между определённым и неопределённым интегралами от непрерывной функции f (x).
Пример 1. Вычислить 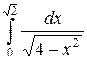 .
.
Решение
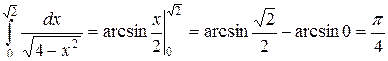 .
.
Пример 2. Вычислить 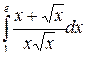 .
.
Решение
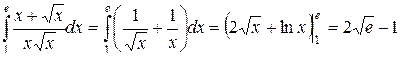 .
.
Пример 3. Вычислить 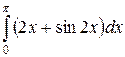 .
.
Решение
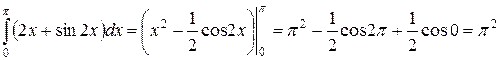 .
.
Пример 4. Вычислить  .
.
Решение
Под знаком интеграла стоит правильная рациональная дробь. Разложим подынтегральную функцию на сумму простейших дробей
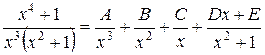 .
.
Освободимся от знаменателя

т. е. 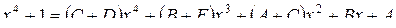 .
.
Сравним коэффициенты при одинаковых степенях  :
:

Находим, что  .
.
Итак,

 .
.
Пример 5. Вычислить 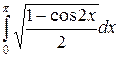 .
.
Решение
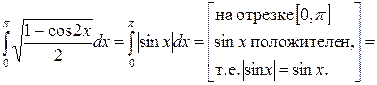
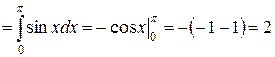 .
.
Пример 6. Вычислить 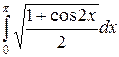 .
.
Решение
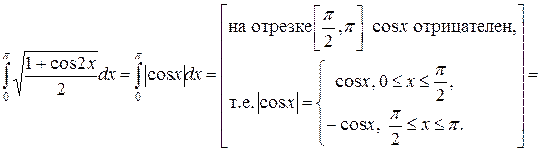
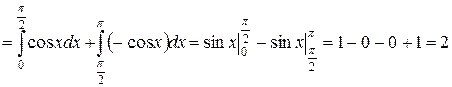 .
.
Пример 7. Вычислить площадь криволинейной трапеции, ограниченной сверху кривой  при
при 
Решение
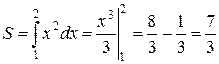 (кв. ед.)
(кв. ед.)
Пример 8. Оценить интеграл 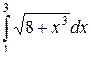 .
.
Решение
Так как подынтегральная функция 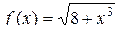 монотонно возрастает на отрезке
монотонно возрастает на отрезке  , то наибольшее и наименьшее значение достигается на концах отрезка
, то наибольшее и наименьшее значение достигается на концах отрезка  . Воспользовавшись свойством 8, получим
. Воспользовавшись свойством 8, получим
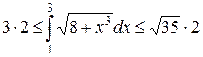 или
или  .
.
Пример 9. Найти двустороннюю оценку интеграла 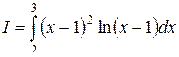 .
.
Решение
Для рассматриваемого интеграла
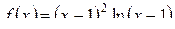 ;
;  ;
;  ;
; 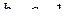 .
.
Для нахождения наибольшего и наименьшего значений функции на отрезке [ a, b ] исследуем функцию на экстремум:
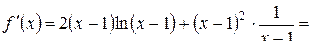
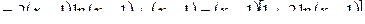 ,
,
 ,
,
 или
или  ,
,
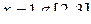
 ,
,
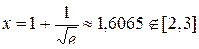 .
.
Следовательно, на [ a, b ] функция f (x) экстремумов не имеет. Определяем значение функции на концах отрезка [ a, b ]:
 ,
,
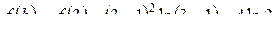 .
.
Значит, 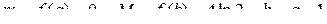 . Воспользуемся свойством 8, получим
. Воспользуемся свойством 8, получим

Задания для самостоятельного решения
Вычислить интегралы:
1. 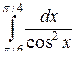 . Ответ.
. Ответ. 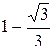 .
.
2. 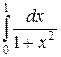 . Ответ.
. Ответ. 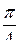 .
.
3. 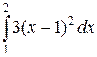 . Ответ. 1.
. Ответ. 1.
4. 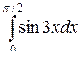 . Ответ.
. Ответ. 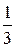 .
.
5. 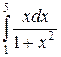 . Ответ.
. Ответ. 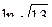 .
.
6. 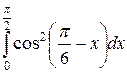 . Ответ.
. Ответ.  .
.
7.  . Ответ.
. Ответ.  .
.
8.  . Ответ. 0.
. Ответ. 0.
2.3.2. Вычисление определённых интегралов
с помощью подстановки
Теорема. Если 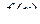
 С
С  ,
, 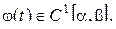 причём функция
причём функция 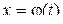 отображает отрезок
отображает отрезок  на отрезок
на отрезок  ,
, 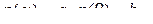
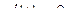 то
то
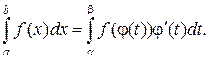
Доказательство
Пусть F (x) – первообразная для f (x), тогда
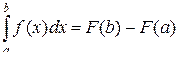 .
.
С другой стороны,
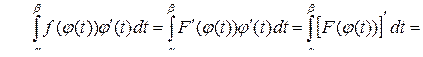
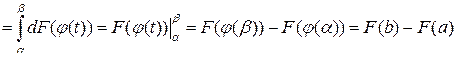 .
.
При вычислении определённого интеграла с помощью подстановки возвращаться к прежней переменной интегрирования не нужно. Однако не следует забывать о необходимости изменения пределов интегрирования.
Пример 1. Вычислить 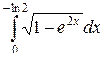 .
.
Решение
Применим подстановку 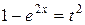 . Выразим
. Выразим 
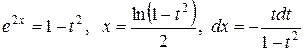 .
.
Найдем новые пределы интегрирования
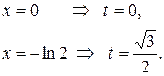
Получим
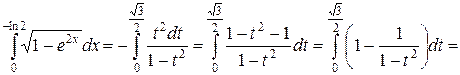
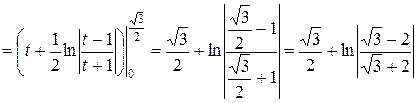 .
.
Пример 2. Вычислить 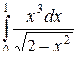 .
.
Решение
Применим подстановку 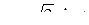 , тогда
, тогда 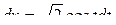 . Найдем новые пределы интегрирования
. Найдем новые пределы интегрирования

Получим
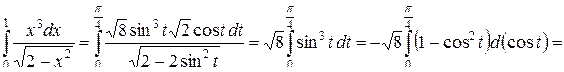

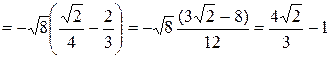 .
.
Пример 3. Вычислить 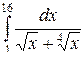 .
.
Решение
Пусть  , тогда
, тогда 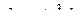 . Новые пределы интегрирования
. Новые пределы интегрирования

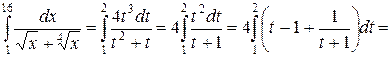
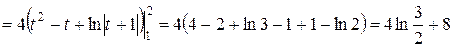 .
.
Пример 4. Вычислить площадь эллипс
|
|
|


