 |
Интегрирование простейших дробей
|
|
|
|
Рациональной дробью называется дробь вида 
, где P (x) и Q (x) – многочлены. Рациональная дробь называется правильной, если степень многочлена P (x) ниже степени многочлена Q (x); в противном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
А. 
.
Б. 
, где m – целое число, большее единицы.
В. 
.
Г. 
, где n – целое число, большее единицы.
Рассмотрим интегралы от простейших дробей:
А. 
.
Б. 
.
Вычисление интегралов от функций типа В было рассмотрено ранее в п. 1.6 «Интегрирование функций, содержащих квадратный трехчлен».
Г. Рассмотрим теперь частный случай интеграла от простейшей дроби типа Г. Для интеграла 
(n – целое положительное число) имеет место следующая рекуррентная формула:
.
Эта формула позволяет после (n -1)-кратного применения свести данный интеграл In к табличному интегралу 
.
Пример 1. Вычислить интеграл
.
Решение
Здесь 
. После первого применения рекуррентной формулы получим
.
К интегралу 
снова применяем рекуррентную формулу (полагаем 
)
.
Итак,
.
Окончательно имеем
.
Покажем теперь в общем виде, как интегрируются простейшие дроби типа Г. Требуется найти 
.
Выделим в числителе производную от квадратного трехчлена, стоящего в знаменателе:
.
Первый интеграл в правой части равенства легко находится при помощи подстановки 
, а второй преобразуем так:
.
Полагая теперь 
и обозначая 
, получаем
.
Таким образом, интегрирование элементарной дроби типа Г может быть выполнено при помощи рекуррентной формулы.
Пример 2. Вычислить интеграл
.
Решение
Имеем
.
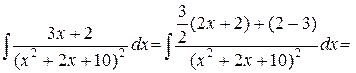
В первом интеграле произведем замену 
, 
, а во втором интеграле положим 
. Отсюда
|
|
|
.
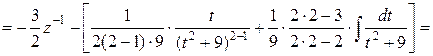
Возвращаясь к старой переменной, получим
.
1.7.2. Интегрирование рациональных дробей с помощью
разложения на простейшие дроби
Интегрирование рациональной дроби проводится по следующему алгоритму:
1) если дана неправильная рациональная дробь, то необходимо выделить из нее целую часть, т. е. представить в виде
,
где M (x) – многочлен, а 
– правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
,
где 
, т. е. трехчлен 
имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби:
4) вычислить неопределенные коэффициенты 
. Для этого привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения.
В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.
Случай 1. Знаменатель имеет только действительные различные корни.
Пример. Вычислить интеграл
.
Решение
Рассмотрим подынтегральную функцию 
– правильная рациональная дробь. Представим ее в виде суммы простейших дробей, разложив знаменатель на множители:
;
.
Приведем к общему знаменателю и рассмотрим числители дробей
.
Полагая, что 
, найдем 
, т. е. 
. Если 
, то получим 
, т. е. 
. При 
получим 
, т. е. 
.
Итак,
.
Случай 2. Знаменатель имеет только действительные корни, причем некоторые из них – кратные.
Пример. Вычислить интеграл
.
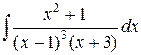Решение
Рассмотрим подынтегральную функцию 
– правильная рациональная дробь. Представим ее в виде суммы простейших дробей. Корни знаменателя – действительные числа, среди них есть кратные (выражению 
соответствует сумма трех простейших дробей).
|
|
|
Таким образом,
.
Приведем к общему знаменателю и рассмотрим числители дробей:
.
Сравним коэффициенты при одинаковых степенях x:
Решая полученную систему уравнений, находим неизвестные коэффициенты
.
Итак,
.
Случай 3. Среди корней имеются простые комплексные корни.
Пример 1. Вычислить интеграл
.
Решение
Рассмотрим подынтегральную функцию 
– неправильная рациональная дробь. Выделим целую часть
.
Представим дробь в виде суммы простейших дробей, разложив знаменатель на множители
.
Тогда
.
Приведем к общему знаменателю и рассмотрим числители дробей
.
Сравним коэффициенты при одинаковых степенях x:
Итак,
.
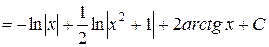Пример 2. Найти интеграл
Решение
Рассмотрим подынтегральную функцию 
– правильная рациональная дробь. Представим в виде суммы простейших дробей. Разложим знаменатель на множители
Тогда
Приведем к общему знаменателю и рассмотрим числители дробей
Воспользуемся комбинированным способом определения коэффициентов. Перепишем предыдущее равенство в виде
Сравнивая коэффициенты при соответствующих степенях и придавая значение 
, получаем систему:
при 
, 
; 
т. е. 
Следовательно,
Случай 4. Среди корней знаменателей имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.
Пример 1. Найти интеграл
.
Решение
Так как в знаменателе есть двукратный множитель, то
.
Приведем к общему знаменателю и рассмотрим числители дробей
.
Приравняем коэффициенты при одинаковых степенях x
Следовательно,
.
Заметим, что данный интеграл можно было найти проще с помощью подстановки 
.
Пример 2. Вычислить интеграл
.
Решение
Выделим целую часть данной неправильной рациональной дроби. Для этого разделим многочлен 
на многочлен 
:
Тогда подынтегральную функцию можно представить в виде суммы целой части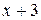 
и дроби, в числителе которой стоит остаток от деления 
:
.
Тогда
.
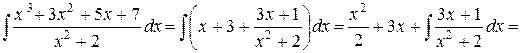
Задания для самостоятельного решения
Вычислить интегралы:
1. 
. Ответ. 
.
2. 
. Ответ. 
.
3. 
. Ответ. 
.
|
|
|
4. 
. Ответ. 
.
5. 
. Ответ. 
.
6. 
. Ответ. 
.
7. 
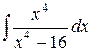. Ответ. 
.
8. 
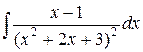. Ответ. 
.
1.8. Интегрирование иррациональных функций
1. Интегралы вида 
, где R – рациональная функция; m 1, n 1, m 2, n 2, … – целые числа
С помощью подстановки 
, где s – наименьшее общее кратное чисел n 1, n 2, …, указанный интеграл преобразуется в интеграл от рациональной дроби.
Пример 1. Вычислить интеграл
.
Решение
.
Пример 2. Вычислить интеграл
.
Решение
Так как наименьшее общее кратное чисел 2, 3, 6 равно 6, то
.
Интегрирование некоторых функций, рационально зависящих от 
, описано ранее в п. 1.6 «Интегрирование функций, содержащих квадратный трехчлен».
2. Интегралы вида 
Такой интеграл приводится к интегралу от рациональной функции новой переменной с помощью следующих подстановок Эйлера.
Первая подстановка Эйлера. Если 
, то полагаем
.
Перед корнем 
возьмем для определенности знак плюс. Тогда
,
откуда x определяется как рациональная функция от t:
(значит, dx тоже будет выражаться рационально через t), следовательно,
,
т. е. 
оказывается рациональной функцией от t.
Так как 
, x и dx выражаются рационально через t, то, следовательно, данный интеграл преобразуется в интеграл от рациональной функции от t.
Пример 1. Вычислить интеграл
.
Решение
Так как 
, то
, 
, 
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
Вторая подстановка Эйлера. Если 
, то полагаем
.
Перед корнем 
возьмем для определенности знак плюс. Тогда
,
откуда x определяется как рациональная функция от t:
.
Так как , x и dx выражаются рационально через t, то, следовательно, данный интеграл преобразуется в интеграл от рациональной функции от t.
Пример 2. Вычислить интеграл
.
Решение
Полагаем 
, тогда
, 
, 
,
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
Третья подстановка Эйлера. Пусть 
и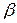 
– действительные корни трехчлена 
. Полагаем
.
Так как 
, то
,
,
.
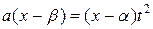Отсюда находим x как рациональную функцию от t:
.
|
|
|
Так как 
, x и dx выражаются рационально через t, то, следовательно, данный интеграл преобразуется в интеграл от рациональной функции от t.
Замечание 1. Третья подстановка Эйлера применима не только при 
, но и при , – лишь бы многочлен 
имел два действительных корня.
Пример 3. Вычислить интеграл
.
Решение
Полагаем 
, тогда
, 
, 
, 
,
, 
.
Подставляя полученные выражения в исходный интеграл, находим
.
Замечание 2. Для приведения исходного интеграла к интегралу от рациональной функции достаточно первой и третьей подстановок Эйлера. Рассмотрим трехчлен 
. Если 
, то корни трехчлена действительны и, следовательно, применима третья подстановка Эйлера. Если 
, то в этом случае
и трехчлен имеет знак, совпадающий со знаком a. Чтобы 
был действительным, нужно, чтобы трехчлен был положительным, а следовательно, должно быть . В этом случае применима первая подстановка.
3. Интегралы вида 
С помощью подстановки 
этот интеграл приводится к рассмотренному в п. 1.8.2.
Пример 1. Вычислить интеграл
.
Решение
.
Пример 2. Вычислить интеграл
.
Решение
.
4. Интегралы от дифференциальных биномов 
, где m, n, p – рациональные числа
Интегралы от дифференциальных биномов выражаются через элементарные функции только в трех случаях:
1) p – целое число; тогда данный интеграл сводится к интегралу от рациональной функции с помощью подстановки 
, где s – наименьшее общее кратное знаменателей дробей m и n;
2) 
– целое число; в этом случае данный интеграл рационализируется с помощью подстановки 
, где s – знаменатель дроби p;
3) 
– целое число; в этом случае к той же цели ведет подстановка 
, где s – знаменатель дроби p.
Пример 1. Вычислить интеграл
.
Решение
Преобразуем подынтегральную функцию
,
т. е. 
– целое число. Значит, имеем первый случай интегрируемости дифференциального бинома. Поэтому следует применить подстановку 
, тогда 
и искомый интеграл принимает вид
.
Возвращаясь к исходной переменной по формуле 
, получим
.
Пример 2. Вычислить интеграл
.
Решение
Переписав подынтегральную функцию в виде 
, имеем 
. Так как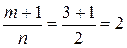 
– целое число, то имеет место второй случай интегрируемости. Используя подстановку 
, получим 
. Следовательно,
.
Пример 3. Вычислить интеграл
.
Решение
Так как 
, то 
– целое число, т. е. пример соответствует третьему случаю дифференциального бинома. Тогда
Задания для самостоятельного решения
Вычислить интегралы:
1. 
. Ответ. 
.
2. 
. Ответ. 
.
3. 
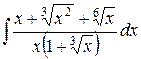. Ответ. 
.
4. 
. Ответ.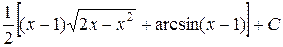 
.
5. 
. Ответ. 
.
6. 
. Ответ. 
.
|
|
|
7. 
. Ответ. 
.
8. 
. Ответ.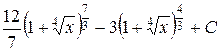 
.
9. 
. Ответ. 
.
1.9. Интегрирование тригонометрических функций
1. Интегралы вида 
, где R – рациональная функция
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью, так называемой универсальной тригонометрической подстановки 
.
В результате этой подстановки имеем
; 
;
.
Пример 1. Вычислить интеграл
Решение
Воспользуемся универсальной тригонометрической подстановкой и приведенными выше формулами:
Пример 2. Вычислить интеграл
Решение
Универсальная тригонометрическая подстановка 
во многих случаях приводит к сложным вычислениям, так как при ее применении 
и 
выражаются через t в виде рациональных дробей, содержащих 
.
В некоторых случаях нахождение интегралов вида 
может быть упрощено:
1) если 
– нечетная функция относительно 
, т. е. если 
, то интеграл вычисляется с помощью подстановки 
;
2) если 
– нечетная функция относительно 
, т. е. если 
, то интеграл вычисляется с помощью подстановки 
;
3) если 
– четная функция относительно 
и 
, т. е. если 
, то к цели приводит подстановка 
.
Пример 3. Вычислить интеграл
Решение
Пример 4. Вычислить интеграл
Решение
Пример 5. Вычислить интеграл
Решение
Пример 6. Вычислить интеграл
Решение
2. Интегралы вида 
Выделим два случая решения такого интеграла:
1) если n – нечетное положительное число, то применяется подстановка 
; если же m – нечетное положительное число, то подстановка 
;
2) если оба показателя степени m и n – четные положительные числа, то следует преобразовать подынтегральную функцию с помощью формул
,
,
.
Пример 1. Вычислить интеграл
Решение
Пример 2. Вычислить интеграл
Решение
Пример 3. Вычислить интеграл
Решение
.
3. Интегралы вида 
и 
, где m – целое положительное число
При нахождении таких интегралов применяются формулы
или 
,
с помощью которых последовательно понижается степень тангенса или котангенса.
Пример 1. Вычислить интеграл
.
Решение
Пример 2. Вычислить интеграл
Решение
Выделим 
и распишем по формуле
4. Интегралы вида 
, 
, 
Тригонометрические формулы
,
,
дают возможность представить произведение тригонометрических функций в виде суммы.
Пример 1. Вычислить интеграл
Решение
Пример 2. Вычислить интеграл
Решение
|
|
|
