 |
Задания для самостоятельного решения
|
|
|
|
Вычислить интегралы:
1.  . Ответ.
. Ответ. 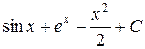 .
.
2.  . Ответ.
. Ответ.  .
.
3. 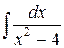 . Ответ.
. Ответ. 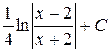 .
.
4.  . Ответ.
. Ответ.  .
.
5. 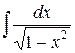 . Ответ.
. Ответ.  .
.
6.  . Ответ.
. Ответ.  .
.
7.  . Ответ.
. Ответ.  .
.
1.4. Замена переменной в неопределенном интеграле. Интегрирование подстановкой
Выполним в интеграле  формальную замену переменной интегрирования
формальную замену переменной интегрирования 
 (1.6)
(1.6)
Проверим полученную формулу, вычислив производные по x от левой и правой частей равенства:



Таким образом, формула (1.6) доказана. При этом считалось, что

Формула (1.6) выражает метод интегрирования подстановкой, или метод замены переменной интегрирования. Этот метод целесообразно использовать в тех случаях, когда интеграл в правой части равенства (1.6) проще, чем в левой. После вычисления нового интеграла приходится возвращаться к старой переменной, для чего находят обратную функцию 
Примеры
1.  =
=  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6. 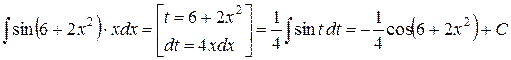 .
.
7.  .
.
8. 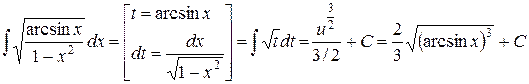 .
.
Подстановки, использованные в приведенных примерах, весьма просты, и их следует научиться выполнять «в уме», не производя записей с переменной t.
Также для решения можно использовать свойство:
 .
.
Доказать его можно с помощью подстановки  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
Задания для самостоятельного решения
Вычислить интегралы:
1.  . Ответ.
. Ответ.  .
.
2.  . Ответ.
. Ответ.  .
.
3. 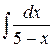 . Ответ.
. Ответ.  .
.
4. 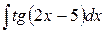 . Ответ.
. Ответ.  .
.
5.  . Ответ.
. Ответ.  .
.
6.  . Ответ.
. Ответ.  .
.
7.  . Ответ.
. Ответ.  .
.
8.  . Ответ.
. Ответ.  .
.
9. 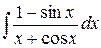 . Ответ.
. Ответ. 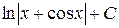 .
.
10. 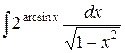 . Ответ.
. Ответ.  .
.
11.  . Ответ.
. Ответ.  .
.
12.  . Ответ.
. Ответ.  .
.
|
|
|
13. 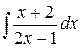 . Ответ.
. Ответ. 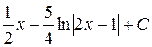 .
.
14.  . Ответ.
. Ответ.  .
.
1.5. Интегрирование по частям
Второй из основных методов интегрирования базируется на формуле, выражающей дифференциал произведения:

Отсюда имеем

или, рассматривая левую и правую части равенства как подынтегральные выражения, получаем
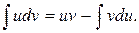 (1.7)
(1.7)
Произвольная постоянная в правой части равенства не пишется.
Формула (1.7) выражает метод интегрирования по частям. Этот метод уместно использовать в тех случаях, когда функция u (x)при дифференцировании упрощается. Поэтому в качестве u (x)выбирают функции  (по возрастанию сложности).
(по возрастанию сложности).
Пример 1. Вычислить интеграл

Решение


 .
.
Пример 2. Вычислить интеграл
 .
.
Решение

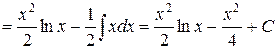 .
.
Иногда, чтобы свести данный интеграл к табличному, приходится применять формулу интегрирования по частям несколько раз. В некоторых случаях с помощью интегрирования по частям получают уравнение, из которого определяется искомый интеграл (такой интеграл называют циклическим).
Пример 3. Вычислить интеграл

Решение


 .
.
Пример 4. Вычислить интеграл
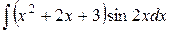 .
.
Решение

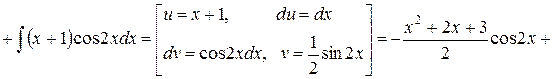
 .
.
Пример 5. Вычислить интеграл

Решение


 .
.
Обозначив исходный интеграл за I, получим уравнение
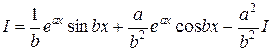 .
.
Решим его относительно I:
 .
.
Тогда
 .
.
Пример 6. Вычислить интеграл
 .
.
Решение
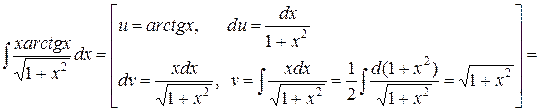

 .
.
Пример 7. Вычислить интеграл
 .
.
Решение
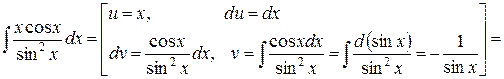
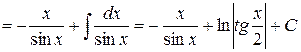 .
.
Следует обратить внимание на то, как усложняется вид функции при действии на неё оператора интегрирования. Это явление является типичным.
Задания для самостоятельного решения
Вычислить интегралы:
1.  . Ответ.
. Ответ.  .
.
2.  . Ответ.
. Ответ. 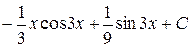 .
.
3. 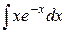 . Ответ.
. Ответ.  .
.
4.  . Ответ.
. Ответ.  .
.
5.  . Ответ.
. Ответ. 
 .
.
6.  . Ответ.
. Ответ.  .
.
7.  . Ответ.
. Ответ.  .
.
8.  . Ответ.
. Ответ.  .
.
|
|
|
1.6. Интегрирование функций,
содержащих квадратный трехчлен
1. Интегралы вида  .
.
Выделим полный квадрат в знаменателе дроби:
 .
.
В зависимости от знака выражения  интеграл сведется
интеграл сведется


Пример 1. Вычислить интеграл
 .
.
Решение
Выделим полный квадрат в знаменателе дроби
 .
.
Тогда
 .
.
Пример 2. Вычислить интеграл
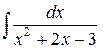 .
.
Решение
Выделим полный квадрат в знаменателе дроби
 .
.
Тогда
 .
.
Пример 3. Найти интеграл

Решение


2. Интегралы вида  .
.
Выделим в числителе производную от знаменателя. Для этого числитель представим в виде
 .
.
Тогда
 .
.
В первом интеграле числитель является производной от знаменателя. Поэтому
 .
.
Второй интеграл рассмотрен в п. 1.
Пример 1. Вычислить интеграл
 .
.
Решение
Имеем


Пример 2. Вычислить интеграл

Решение
Преобразуем знаменатель
 .
.
Тогда

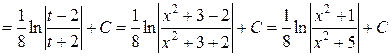 .
.
3. Интегралы вида  .
.
Выделим полный квадрат в подкоренном выражении
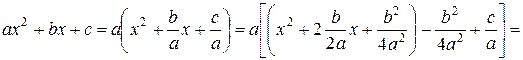

Интеграл сведется к табличным интегралам 15 или 16.
Пример 1. Вычислить интеграл
 .
.
Решение
Выделим полный квадрат в подкоренном выражении
 .
.
Тогда
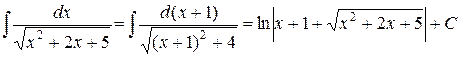 .
.
Пример 2. Вычислить интеграл
 .
.
Решение
Преобразуем квадратный трехчлен к виду

 .
.
Тогда


4. Интегралы вида  .
.
Для нахождения этого интеграла выделим в числителе производную квадратного трехчлена, стоящего под знаком корня, и разложим интеграл на сумму двух интегралов


Первый из интегралов есть табличный интеграл
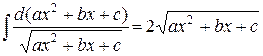 ,
,
а второй рассмотрен в п. 3.
Пример 1. Вычислить интеграл
 .
.
Решение
Выделим в числителе производную от подкоренного выражения



Пример 2. Вычислить интеграл
 .
.
Решение
Выделим в числителе производную от подкоренного выражения



Задания для самостоятельного решения
Вычислить интегралы:
1.  . Ответ.
. Ответ.  .
.
2.  . Ответ.
. Ответ.  .
.
3.  . Ответ.
. Ответ.  .
.
4. 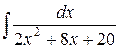 . Ответ.
. Ответ.  .
.
5.  . Ответ.
. Ответ.  .
.
6.  . Ответ.
. Ответ.  .
.
7.  . Ответ.
. Ответ. 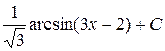 .
.
8.  . Ответ.
. Ответ. 
 .
.
1.7. Интегрирование рациональных дробей
|
|
|


