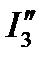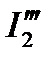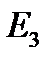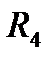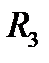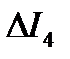Основные теоретические положения
Принцип суперпозиции (наложения) является одним из важнейших физических принципов, отражающих основное свойство линейных систем – независимость действия возбуждающих сил.
Этот принцип используется при рассмотрении явлений, возникающих под воздействием нескольких причин. В соответствии с этим принципом сложные явления подразделяются на более простые, в которых каждая причина действует независимо от других, а результаты воздействий, накладываясь один на другой, образуют суммарный эффект.
Этот принцип можно применить только к линейным цепям. Его формулируют следующим образом: Ток через любой элемент электрической цепи (напряжение на нем) равен алгебраической сумме частичных токов через этот же элемент (частичных напряжений на нем), вызванных действием каждого источника энергии в отдельности.
При анализе сложных электрических цепей принцип суперпозиции используется для того, чтобы воздействие нескольких источников электрической энергии на данный элемент цепи можно было рассматривать как результат воздействия на этот элемент каждого из источников в отдельности.
Отметим, что принцип суперпозиции применяется также для того, чтобы результат воздействия одной ЭДС сложной формы можно было заменить воздействием составляющих ЭДС более простых форм.
Применяя принцип суперпозиции, можно найти ток любой ветви или напряжение любого участка линейной электрической цепи как алгебраическую сумму частичных токов или напряжений, вызываемых отдельным действием источников ЭДС и тока. С помощью принципа суперпозиции (наложения) расчёт сложной цепи с несколькими источниками ЭДС и тока можно свести к расчёту нескольких цепей с одним источником.
Выбирая, поочерёдно, следующий источник энергии для расчёта частичных токов, остальные источники из схемы устраняют. При этом, устраняя источники ЭДС, оставляют их внутренние сопротивления, устраняя источники тока – их внутренние проводимости; место включения источника ЭДС закорачивают, место соединения источника тока разрывают. На рис. 1 – 4 показано, как устраняются из схемы идеальный (рис. 1) и реальный (рис. 2) источники ЭДС, а также идеальный (рис. 3) и реальный (рис. 4) источники тока.
Рассмотрим схему электрической цепи (рис. 5), в которой имеется три источника ЭДС. Для определения токов в такой цепи вначале полагают, что в ней действует только источник ЭДС  . Сопротивления всех элементов считают неизменными. Определение частичных токов
. Сопротивления всех элементов считают неизменными. Определение частичных токов  отдельных ветвей от действия источника ЭДС
отдельных ветвей от действия источника ЭДС  сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов
сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов  от действия источника ЭДС
от действия источника ЭДС  в соответствии со схемой рис.7. и частичных токов
в соответствии со схемой рис.7. и частичных токов  от действия источника ЭДС
от действия источника ЭДС  по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей:
по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей:
 . (1)
. (1)
Как видно, метод расчёта электрических цепей с использованием принципа суперпозиций является довольно громоздким и поэтому применяется редко. Он целесообразен тогда, когда электрическое состояние цепи определено для каких – либо источников ЭДС и токов и требуется проанализировать электрическое состояние цепи при изменении ЭДС или тока одного из источников. В этом случае нет необходимости вновь рассчитывать значения токов и напряжений от действия всех источников, а достаточно определить лишь частичные токи и напряжения от действия дополнительной ЭДС  или дополнительного тока
или дополнительного тока  источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении
источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении 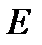 или
или  .
.
Пример: На схеме замещения электрической цепи (рис. 9) при заданных значениях  и
и  известны токи всех ветвей:
известны токи всех ветвей:  ,
, 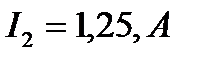 ,
,  ,
, 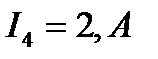 . Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС
. Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС 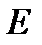 в 2 раза, т. е. при новых значениях ЭДС
в 2 раза, т. е. при новых значениях ЭДС 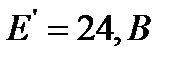 и
и 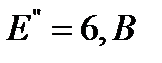 . Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС
. Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС  и
и  в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС
в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС  равны:
равны:  ,
,  ,
,  . Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС
. Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС  . После увеличения ЭДС токи примут значения:
. После увеличения ЭДС токи примут значения:
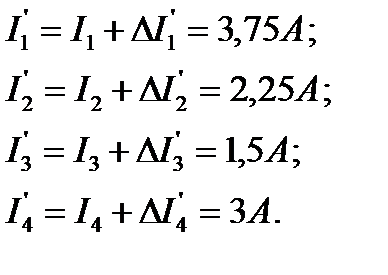
От действия ЭДС  частичные токи будут иметь значения:
частичные токи будут иметь значения:  ,
,  , а новые значения токов в ветвях при уменьшении ЭДС
, а новые значения токов в ветвях при уменьшении ЭДС 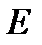 в 2 раза составят:
в 2 раза составят:  ,
,  ,
,  ,
, 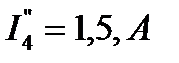 . Следует обратить внимание на то, что ток
. Следует обратить внимание на то, что ток  . Это произошло вследствие того, что потенциалы точек
. Это произошло вследствие того, что потенциалы точек  и
и  в схеме рис. 10 при новом значении ЭДС
в схеме рис. 10 при новом значении ЭДС  оказались равными
оказались равными

В заключении подчеркнём, что метод суперпозиций не применим для расчёта мощностей элементов цепи, так как их значения пропорциональны квадратам токов.
Порядок выполнения работы
1. Ознакомиться с приборами, необходимыми для выполнения работы и записать основные технические данные измерительных приборов, источников питания и реостатов.
2. Провести измерение сопротивлений шести реостатов, необходимых для выполнения лабораторной работы. Для этого собрать цепь по схеме на рис. 11, используя один из требуемых для работы источников. Каждый раз, подключая новый реостат при замкнутом ключе и снимая показания измерительных приборов, вычислить (в последствии) его сопротивление (методом амперметра (pA1) и вольтметра (pV1)). При необходимости по указанию преподавателя, меняя положение ползунка реостата, подобрать требуемое значение сопротивления этого реостата. Результаты измерений и вычислений занести в таблицу 1.
3. Определить ЭДС и внутреннее сопротивление каждого источника. Для этого использовать прежнюю электрическую цепь (рис. 11). Используя ее для первого (произвольного) источника, снять показания приборов при замкнутом и разомкнутом ключе К. При этом показания вольтметра pV1 при разомкнутом ключе ( ) определяют величину ЭДС этого источника
) определяют величину ЭДС этого источника
 .
.
Показания приборов (pV1 и pA1) при замкнутом ключе ( ) позволяют рассчитать внутреннее сопротивление источника
) позволяют рассчитать внутреннее сопротивление источника
 .
.
Аналогично определить внутреннее сопротивление второго источника. Занести результаты измерений и вычислений в табл. 2.
4. Собрать цепь по схеме на рис. 12, провести три опыта:
а) опыт №1: ключ  – в положении «а», ключ
– в положении «а», ключ  – в положении «б»;
– в положении «б»;
б) опыт №2: ключ  – в положении «б», ключ
– в положении «б», ключ  – в положении «а»;
– в положении «а»;
в) опыт №3: ключи  и
и  – в положении «а».
– в положении «а».
Результаты измерений занести в табл. 3.
5. Для электрической цепи третьего опыта составить эквивалентную схему замещения, в которой по известным величинам 
 определить токи в каждой ветви методом наложения. результаты вычислений занести в табл. 3 и сравнить полученные результаты с данными опыта №3.
определить токи в каждой ветви методом наложения. результаты вычислений занести в табл. 3 и сравнить полученные результаты с данными опыта №3.
ЛИТЕРАТУРА
1. Касаткин А. С., Немцов Н. В. Электротехника: учебное пособие для ВУЗов. М.: Издательский центр «Академия», 2005 (подраздел 1.15).
2. Борисов Ю. М., Липатов Д. Н., Зорин Ю. Н. Электротехника: Учебное пособие для ВУЗов. М.: Энергоатомиздат, 1985 (подраздел 1.14.4).
3. Электротехника: Учебник для неэлектрических специальностей ВУЗов / Под редакцией В. Г. Герасимова. М.: Высшая школа, 1985 (подразделы 1.7; 1.11).
4. Общая электротехника: Учебное пособие для ВУЗов / Под редакцией А. Т. Блажина. Л.: Энергоатомиздат, 1986 (подраздел 1.6).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чём заключается сущность принципа наложения?
2. Как производится расчёт электрических цепей методом наложения?
3. В каких случаях для расчёта сложной цепи целесообразно применять метод наложения?
4. Применим ли метод наложения для расчёта электрической мощности цепи?
5. Как устраняются из схемы активные элементы при расчёте методом наложения? Проиллюстрировать на примере.
Рис. 1. Рис. 2.
Рис. 3. Рис. 4.
Рис. 5.
Рис. 6.
Рис. 7.
Рис. 8.
Рис. 9.
Рис. 10.
Рис. 11.
Таблица 1
Воспользуйтесь поиском по сайту:


 . Сопротивления всех элементов считают неизменными. Определение частичных токов
. Сопротивления всех элементов считают неизменными. Определение частичных токов  отдельных ветвей от действия источника ЭДС
отдельных ветвей от действия источника ЭДС  сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов
сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов  от действия источника ЭДС
от действия источника ЭДС  в соответствии со схемой рис.7. и частичных токов
в соответствии со схемой рис.7. и частичных токов  от действия источника ЭДС
от действия источника ЭДС  по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей:
по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей: . (1)
. (1) или дополнительного тока
или дополнительного тока  источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении
источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении 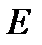 или
или  .
. и
и  известны токи всех ветвей:
известны токи всех ветвей:  ,
, 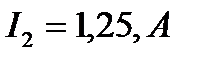 ,
,  ,
, 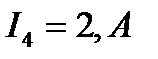 . Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС
. Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС 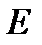 в 2 раза, т. е. при новых значениях ЭДС
в 2 раза, т. е. при новых значениях ЭДС 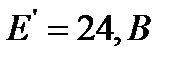 и
и 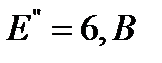 . Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС
. Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС  и
и  в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС
в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС  равны:
равны:  ,
,  ,
,  . Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС
. Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС  . После увеличения ЭДС токи примут значения:
. После увеличения ЭДС токи примут значения: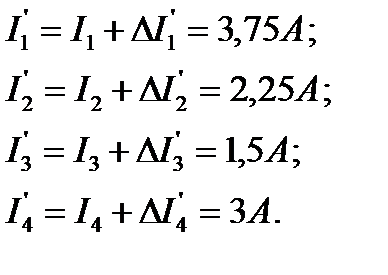
 частичные токи будут иметь значения:
частичные токи будут иметь значения:  ,
,  , а новые значения токов в ветвях при уменьшении ЭДС
, а новые значения токов в ветвях при уменьшении ЭДС 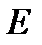 в 2 раза составят:
в 2 раза составят:  ,
,  ,
,  ,
, 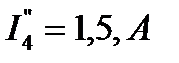 . Следует обратить внимание на то, что ток
. Следует обратить внимание на то, что ток  . Это произошло вследствие того, что потенциалы точек
. Это произошло вследствие того, что потенциалы точек  и
и  в схеме рис. 10 при новом значении ЭДС
в схеме рис. 10 при новом значении ЭДС  оказались равными
оказались равными
 ) определяют величину ЭДС этого источника
) определяют величину ЭДС этого источника .
. ) позволяют рассчитать внутреннее сопротивление источника
) позволяют рассчитать внутреннее сопротивление источника .
. – в положении «а», ключ
– в положении «а», ключ  – в положении «б»;
– в положении «б»; – в положении «б», ключ
– в положении «б», ключ  – в положении «а»;
– в положении «а»; и
и  – в положении «а».
– в положении «а».
 определить токи в каждой ветви методом наложения. результаты вычислений занести в табл. 3 и сравнить полученные результаты с данными опыта №3.
определить токи в каждой ветви методом наложения. результаты вычислений занести в табл. 3 и сравнить полученные результаты с данными опыта №3.