 |
В комплексной форме записи
|
|
|
|
Первый закон Кирхгофа. Имеем цепь, в которой действуют ЭДС, напряжения и протекают токи синусоидальные по форме зависимости от времени, к тому же эти параметры имеют одинаковую частоту. Выделим произвольный узел, в котором сходится 
ветвей и, соответственно, синусоидальных токов
………………………….;
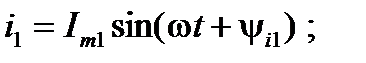
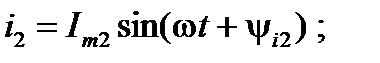
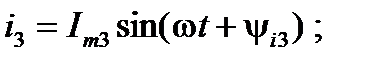
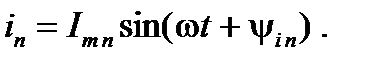
В соответствии с первым законом Кирхгофа для данного узла можно составить уравнение в мгновенной форме записи
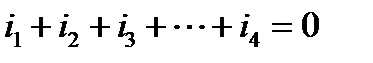. (21)
Учитывая установленное ранее взаимнооднозначное соответствие между синусоидальными токами и их изображениями на комплексной плоскости в виде комплексов действующих значений, сумму токов можно заменить суммой комплексных векторов
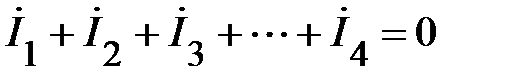. (22)
Выражение (22) представляет собой одну из форм записи первого закона Кирхгофа в комплексной форме. Условно эту форму можно интерпретировать следующим образом. Алгебраическая сумма комплексов действующих значений синусоидальных токов в узле цепи равна нулю.
Второй закон Кирхгофа. Выделим в указанной цепи некоторый контур, в который включены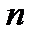 
пассивных элементов (
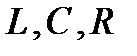) и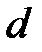 
источников синусоидальной ЭДС. В соответствии со вторым законом Кирхгофа для данного контура можно записать
.
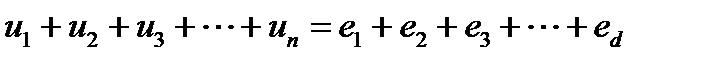Аналогичным образом, учитывая установленное ранее взаимнооднозначное соответствие между синусоидальными напряжениями, ЭДС и их изображениями на комплексной плоскости в виде комплексов действующих значений, сумму мгновенных значений этих параметров можно заменить суммой комплексных векторов
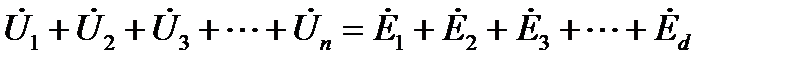. (23)
Выражение (23) представляет собой одну из форм записи второго закона Кирхгофа в комплексной форме. Условно эту форму можно интерпретировать следующим образом. Алгебраическая сумма комплексов действующих значений синусоидальных напряжений на пассивных элементах в любом контуре цепи равна алгебраической сумме комплексов действующих значений синусоидальных ЭДС в этом же контуре.
|
|
|
Закон Ома. Выделим в некоторой цепи синусоидального тока участок, через который протекает синусоидальный ток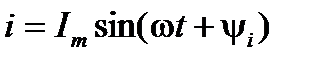 
и к этому участку приложено синусоидальное напряжение 
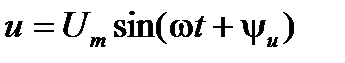. Учитывая взаимно-однозначное соответствие между этими синусоидальными параметрами и изображающими их на комплексной плоскости векторами, мгновенные значения этих параметров можно заменить комплексными векторами (комплексами действующих значений)
;
.
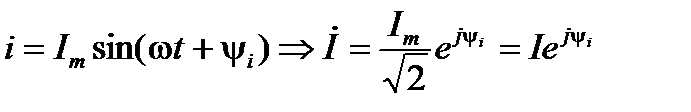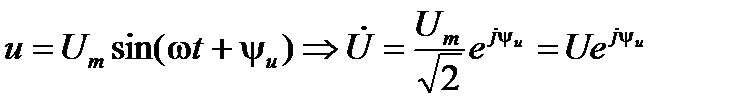Возьмем формальное отношение комплексных векторов
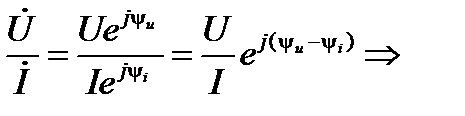
отношение можно интерпретировать как сопротивление указанного участка, поскольку численное равенство между напряжением, током и модулем соответствующего вектора соблюдается. Разность начальных углов векторов численно равную разности начальных фаз напряжения и тока, можно интерпретировать как разность или сдвиг фаз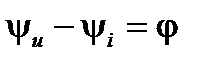 
. В таком случае
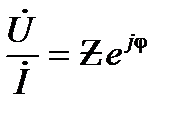(24)
или
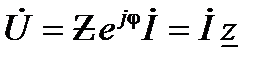. (25)
Выражения (24) и (25) определяют закон Ома в комплексной форме для пассивного участка цепи. В них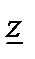 
– комплексное сопротивление данного участка цепи, 
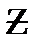– полное сопротивление этого участка (в литературе это сопротивление также обозначают как 
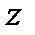). В соответствии с формами записи комплексную величину 
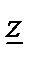можно представить в алгебраической
,
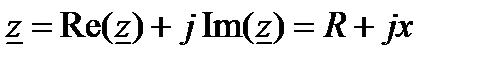тригонометрической
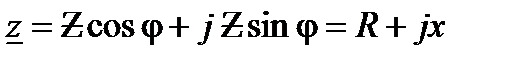
или в показательной форме записи
.
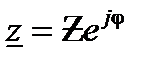В электротехнике составляющие комплексного сопротивления имеют специфические определения. Так, полное сопротивление участка цепи выражается через составляющие комплексного сопротивления
,
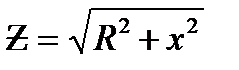где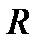 
– определяется как активное сопротивление участка цепи, 
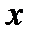– реактивное сопротивление этого участка, угол 
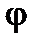, определенный как разность фаз между синусоидами напряжения и тока, в данном случае имеет еще дополнительное определение и обозначается как фазовый угол полного сопротивления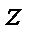 
|
|
|
.
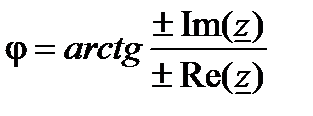При вычислении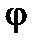 
необходимо учитывать знаки составляющих комплексного сопротивления, которые определяют, в какой четверти лежит этот угол.
Возьмем противоположное формальное отношение
,
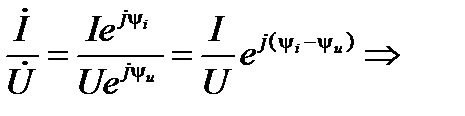рассуждая аналогично, получим
.
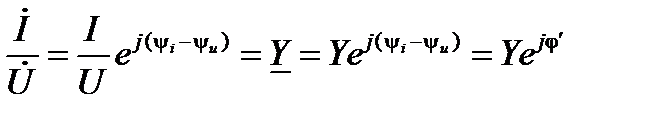Окончательно
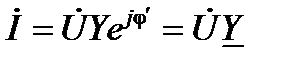, (26)
где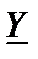 
– комплексная проводимость участка цепи; 
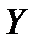– полная проводимость этого участка (в литературе этот параметр также обозначают как 
); 
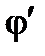– угол сдвига фаз между синусоидами тока и напряжения, а также фазовый угол полной проводимости.
В соответствии с формами записи комплексную величину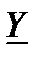 
можно представить в алгебраической
,
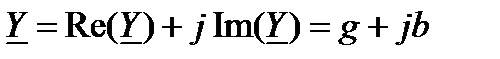тригонометрической
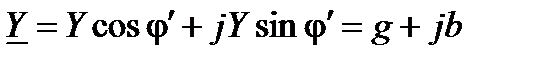
или в показательной форме записи
.
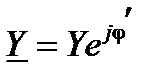В электротехнике составляющие комплексной проводимости имеют специфические определения. Так, полная проводимость участка цепи выражается через составляющие комплексной проводимости
,
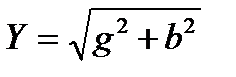где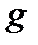 
– определяется как активная проводимость участка цепи, 
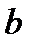– реактивная проводимость этого участка, угол 
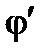определяется, например, так
.
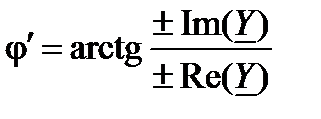При вычислении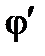 
необходимо учитывать знаки составляющих комплексной проводимости, которые определяют, в какой четверти лежит этот угол.
По аналогии записывается закон Ома для замкнутой цепи
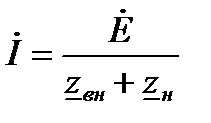, (27)
где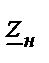 
– комплексное сопротивление нагрузки; 
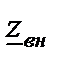– комплексное внутреннее сопротивление источника энергии.
Приведем формулу обобщенного закона Ома в комплексной форме записи
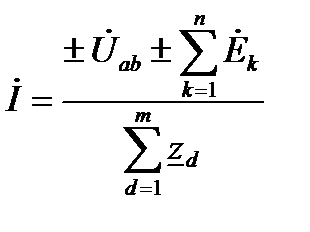, (28)
где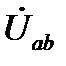 
– напряжение на рассматриваемом участке цепи; 
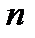– количество источников ЭДС, включенных на этом участке; 
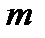– количество пассивных элементов на этом участке.
ПРИМЕЧАНИЕ. Во всех формулах, отражающих законы цепей в комплексной форме, знаки слагаемых определяются по тем же правилам, что и для цепей постоянного тока (см. лаб. раб. №1). О знаках комплексных сопротивлений будет сказано ниже.
Величины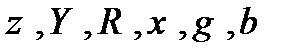 
существуют реально (их можно измерить). В связи с чем они имеют свои размерности.
|
|
|
.
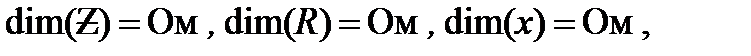
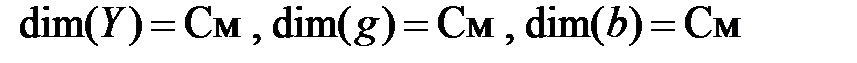Комплексным величинам присвоены соответствующие единицы измерения условно.
.
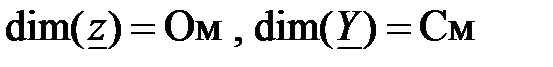Таким образом, метод расчета цепей синусоидального тока, основанный на использовании комплексных векторов называется символическим. Его проводят в следующем порядке:
· важным условием осуществимости этого метода расчета является линейность схемы замещения электрической цепи и одинаковая частота всех источников синусоидальных ЭДС, включенных в схему;
· все заданные параметры схемы (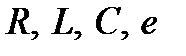
) и искомые параметры режима работы (
) представляют в комплексной форме записи;
· используя законы цепей в комплексной форме, составляют систему расчетных уравнений относительно неизвестных комплексных параметров режима работы. Можно использовать любой из известных методов (метод законов Кирхгофа, метод наложения, метод контурных токов, метод узловых потенциалов, метод двух узлов, метод эквивалентного генератора). Порядок составления уравнений и знаки слагаемых в уравнениях полностью отвечают использованию этих методов для цепей постоянного тока;
· решая полученную систему уравнений, определяют неизвестные параметры режима работы (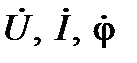
). При необходимости рассчитывают мощность или энергию на рассматриваемых участках цепи, используя закон Джоуля-Ленца в комплексной форме записи.
· при необходимости наглядной интерпретации результатов расчета строят так называемые векторные диаграммы, а также представляют рассчитанные параметры в виде синусоидальных функций времени в аналитическом или графическом виде.
Далее рассмотрим основы символического метода расчета. Начнем с рассмотрения элементарных моделей участков цепи.
|
|
|
