 |
Участок цепи с резистивным элементом
|
|
|
|
Резистивным (или 
-элементом) называют такой элемент схемы замещения (расчетной схемы), который способен лишь безвозвратно потреблять энергию электрического тока, преобразуя её в неэлектрические виды энергии (например, в тепловую с рассеянием её в окружающее пространство). Другими энергетическими свойствами эта модель не обладает. Её реальными прообразами являются, например, нагревательные элементы электрической печи, лампы накаливания, а также специальные элементы электронных схем – резисторы. Однако эти прообразы обладают многими другими физическими свойствами, не являющимися для них основными, поэтому в модели эти свойства не учитываются.
Преобразование энергии на резистивном элементе происходит в результате того, что он оказывает сопротивление протекающему через него электрическому току. Количественной мерой такого сопротивления служит параметр резистивного элемента, обозначаемый 
и 
и называемый электрическим сопротивлением. Этот параметр измеряется в Омах. Для резистивного элемента его параметр 
, протекающий через него ток 
и падение напряжения на выводах этого элемента 
(рис.5) связаны законом Ома:
|
|
|
Рис. 5.
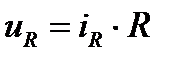; (29)
. (30)
Величина 
– называется проводимостью резистивного элемента. Единицей измерения служит сименс. Если 
и не зависит от 
и 
, то резистивный элемент – линейный и как видно из (29), зависимость тока от времени будет подобна зависимости от времени напряжения. Мгновенная мощность для цепи с резистивным элементом:
или, учитывая (29), получим
.
Мгновенная мощность, как скорость изменения электрической энергии на рассматриваемом участке цепи, измеряется в ваттах (Вт).
|
|
|
Пусть через резистивный элемент протекает синусоидальный ток:
.
Выберем (рис.5) положительные направления для 
и 
совпадающими, тогда в соответствии с (29) можно записать
. (31)
Из (31) видно, что 
.
Т.е. в цепи с линейным резистивным элементом при синусоидальном токе падение напряжения на этом элементе также синусоидально и совпадает по фазе с током (рис.6). Из (31) можно записать закон Ома для амплитудных 
и, учитывая, что 
и 
, для действующих значений напряжения и тока:
. (32)
Можно записать (32) в комплексной форме. Для этого перейдем от синусоидальных 
и 
к однозначно соответствующим им комплексам действующих значений
; 
.
| u (t) |
|
| 0 |
| U∙I |
| U∙I |
| p (t) |
| u,i |
| i (t) |
| ω t |
| ω t |
| p |
Рис. 6.
Если 
, тогда
,
но согласно (32)
.
Следовательно,
или
(33)
Соотношение (33) представляет собой закон Ома для участка цепи с резистивным элементом в комплексной форме
Построим векторную диаграмму для данного участка цепи (рис.7).
|
|
|
|
|
|
|
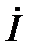
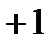
Рис. 7.
Построение начинаем с выбора масштабов по току 
(А/см) и напряжению 
(В/см). Затем строим заданный вектор тока. Для этого откладываем от оси 
угол 
в соответствии с его знаком (против часовой стрелки, т.к. 
см. рис.6) и проводим луч 
. На этом луче 
в масштабе 
откладываем отрезок длиной 
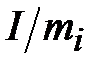(см) от т.0 (
– действующее значение тока). Другой конец отрезка обозначаем стрелкой. Вектор 
построен. Поскольку 
, то вектор напряжения будет также лежать на луче . Для построения вектора 
от т.0 в масштабе 
откладываем отрезок равный 
(см), другой конец отрезка отмечаем стрелкой. Вектор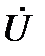 
построен (
– действующее значение напряжения). На этом завершается построение диаграммы для данного участка цепи.
|
|
|
Рассмотрим энергетические процессы, протекающие в цепи с 
-элементом.
Тот факт, что ток и напряжение в цепях синусоидального тока в течение периода изменяют своё направление на противоположное, не лишает смысла наличия стрелок положительных направлений (рис.5): истинное направление тока (напряжения) совпадает со стрелкой в те моменты, когда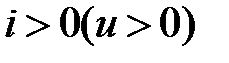 
и противоположно стрелке, если 
. Важно то, что на линейном резистивном элементе напряжение и ток всегда совпадают по направлению.
Тогда мгновенная мощность 
будет всегда величиной положительной (рис. 6), т.е. 
-элемент только потребляет электрическую энергию от источника и преобразует её в другие неэлектрические виды. Определим зависимость 
(34)
.
Т.о. с течением времени мощность колеблется с частотой 
в пределах от 
до 
вокруг среднего значения, равного 
(рис.6), и в любой момент времени 
.
Среднее значение мощности за период называют активной мощностью и обозначают буквой 
. (35)
С учётом (22) выражение (25) можно записать в виде
. (36)
Активная мощность не только на участке цепи с 
-элементом, но и в целом в любой цепи характеризует работу, совершаемую электрической энергией за период, т.е. определяет энергию 
, необратимо преобразующуюся в другие неэлектрические виды энергии:
.
На рис.6 этой работе соответствует заштрихованная площадь, ограниченная кривой 
и осью абсцисс. Единицей измерения активной мощности является Ватт/Вт/.
|
|
|
