 |
Основные одномерные параметризации.
|
|
|
|
ГЛАВА 1. ARCH ПРОЦЕССЫ. ОПРЕДЕЛЕНИЕ, МОДЕЛИ, ПРИЛОЖЕНИЯ.
Если задано распределение вероятностей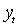 
, условное по предопределенным к моменту t величинам 
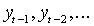, составляющим информационное множество 
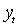, то одношаговым прогнозом значения на основе этой информации является условное математическое ожидание 
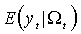, ошибкой прогноза – условная дисперсия 
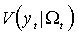. Оба этих выражения в принципе допускают зависимость от 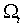. Если же условная дисперсия в действительности постоянна и не зависит от истории процесса, то такой процесс обладает свойством условной гомоскедастичности.
Рассмотрим в качестве примера авторегрессию
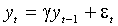
где e - белый шум с дисперсией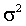 
. Условное среднее равно 
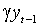, тогда как условная дисперсия равна 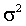и не зависит от истории процесса, который является поэтому условно гомоскедастичным. Являются таковыми и все процессы авторегрессии – скользящего среднего.
Известно, что вариабельность экономических переменных широко изменяется во времени, соответственно, изменяется и точность эконометрических прогнозов. Гипотеза гомоскедастичности остатков, как правило, не выдерживает тестирования. Ниже изучаются процессы, обладающие свойством условной гетероскедастичности, т.е. такие, условная дисперсия которых нетривиально зависит от истории процесса и более точно характеризует степень присущей прогнозам неопределенности.
ОПРЕДЕЛЕНИЕ
Пусть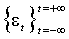 
– скалярный стохастический процесс, 
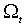– набор переменных, которым обусловлены математические ожидания:
,
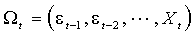где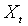 
- экзогенные переменные. Процесс e является авторегрессионно условно гетероскедастичным (Autoregressive Conditionally Heteroskedastic, ARCH), если
(1.1.а)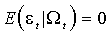 
(1.1.б)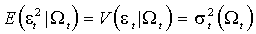 
и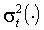 
нетривиально зависит от 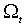; аргумент функции далее будем опускать. Данное определение будет уточнено в последующих параграфах.
|
|
|
Лишь немногие экономические переменные имеют постоянное условное среднее, равное нулю. Как правило, процесс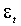 
соответствует возмущениям менее ограничительной модели какой-либо переменной 
:
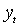(1.2)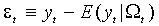 
.
В этом случае условные дисперси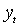и и 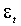совпадают.
Стандартизованный процесс
(1.3)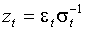 
имеет неизменные во времени нулевое условное среднее и единичную условную дисперсию.
Приведенное определение охватывает чрезвычайно широкий класс процессов. Ниже рассматриваются некоторые возможные параметризации условной дисперсии.
Пусть, например,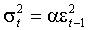 
, a > 0. Тогда при a < 1 безусловная дисперсия равна нулю, при a > 1 бесконечна. Такие свойства безусловного распределения 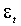делают данную параметризацию непривлекательной, однако некоторые обобщения позволяют избежать подобных проблем.
GARCH
В формулировке, предложенной Энглом (Engle, 1982), условная дисперсия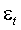 
описывается линейной функцией квадратов предшествующих 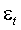реализаций ряда:
(1.4)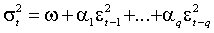 
.
Для того, чтобы эта величина оставалась положительной с вероятностью единица, требуется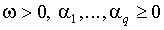 
.
Высокие по абсолютному значению реализации процесса в непосредственном прошлом влекут увеличение условной дисперсии в данный момент, и, следовательно, условной вероятности появления вновь высокой по модулю реализации e. Напротив, относительно небольшие значения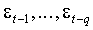 
приводят к снижению этой вероятности. Таким образом, можно ожидать, что вслед за большими (по абсолютному значению) наблюдениями вновь последуют большие наблюдения, за малыми - малые. Выбросы имеют тенденцию следовать один за другим, формируя периоды экстремально высокой волатильности. История процесса, однако, не позволяет прогнозировать знак 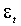, поскольку ряд серийно не коррелирует. Серийная некоррелированность следует из требования (1.1.а), традиционно предъявляемого к возмущениям в эконометрической модели.
|
|
|
На графике ARCH процесса могут быть обнаружены периоды спокойного движения переменной, характеризующиеся относительно низкой дисперсией, и турбулентные периоды, в течение которых дисперсия высока. В западной литературе такое поведение временного ряда получило название clustering volatility: образование “пучков”, концентрация волатильности. Термин “волатильность” (volatility - изменчивость, непостоянство, англ.) используется, как правило, для неформального обозначения степени вариабельности, разброса переменной. Формальной мерой волатильности служит дисперсия (или стандартное отклонение). Эффект clustering volatility отмечен для многих высокочастотных рядов, таких как изменение цен акций, валютных курсов, доходности спекулятивных активов. Наиболее цитируемым в данной связи является наблюдение Манделброта (Mandelbrot, 1963):
“...большие изменения имеют тенденцию следовать за большими изменениями - любого знака, - и малые изменения имеют тенденцию следовать за малыми,...”.
На рисунке 1 изображены темпы приростов фондового индекса РТС. Имеются три ярко выраженных и продолжительных всплеска волатильности, которые чередуются с периодами относительно предсказуемого развития переменной; в целом РТС демонстрирует поведение, характерное для ARCH процесса.
Память ARCH (q) процесса ограничена q периодами. При использовании модели часто требуется длинный лаг q и большое число параметров a. Обобщенный ARCH процесс (Generalized ARCH, GARCH), предложенный Т. Боллерслевом (Bollerslev, 1986), имеет бесконечную память и допускает более экономную параметризацию:
(1.5)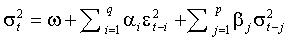 
.
ARCH процесс, очевидно, является частным случаем (1.5). Помимо (1.5), часто используются следующие представления процесса:
- При помощи оператора сдвига L и многочленов
:
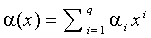
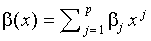(1.6)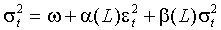 
.
- В виде процесса авторегрессии – скользящего среднего. Перегруппировав члены (1.6), приходим к уравнениям
(1.7)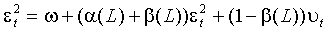 
,
,
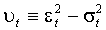которые говорят о том, что квадраты ошибок подчиняются ARMA модели с полиномом авторегрессии a (x) + b (x) степени pÙ q, полиномом скользящего среднего -b (x) степени p и серийно некоррелированными инновациями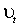 
. Для ARCH процесса (при p= 0) представление (1.7) сводится к авторегрессии порядка q:
.
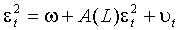- В виде распределенного лага значений
.
|
|
|
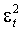
(1.8)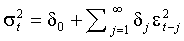 
.
Такое представление допустимо, если все корни 1-b (x) лежат вне единичного круга и не совпадают с корнями a (x). Полином бесконечной степени, участвующий в (1.8), соответствует разложению в ряд Тейлора a (x)/(1-b (x)). GARCH процесс является корректно определенным, лишь если все коэффициенты d данного разложения неотрицательны, что для GARCH (1,1) равносильно условию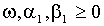 
.
EGARCH
Простая структура GARCH модели существенно ограничивает динамику временного ряда. Как правило, указывается на три недостатка моделей данного типа.
I. Отмечено, что отдача вложений в акции имеет отрицательную корреляцию с изменениями волатильности. Благодаря предложенному экономическому объяснению феномен получил название “левередж-эффекта” (leverage effect). Снижение рыночной стоимости акционерного капитала увеличивает отношение заемных средств к собственным и, следовательно, повышает рискованность вложений в фирму. Последнее проявляется увеличением волатильности. В результате, будущие значения волатильности отрицательно коррелируют с текущей отдачей. Nelson (1991) описывает феномен таким образом:
‘‘Отрицательные инновации, или “плохие новости” – ситуация, в которой фактическая отдача ниже ожидаемой – приводят к увеличению волатильности. Напротив, положительные инновации (“хорошие новости” – фактическая отдача выше ожидаемой) влекут снижение волатильности.’’
Речь идет, таким образом, об отрицательной корреляции между 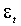и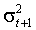 
. Корреляция между этими величинами, однако, игнорируется GARCH моделью. Действительно, 
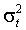есть функция собственных лагов и значений 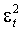и поэтому инвариантна к изменениям алгебраического знака 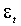: лишь абсолютные значения, но не отрицательность или положительность ошибок определяют условную дисперсию. Если распределение e симметрично, то будущее значение условной дисперсии не коррелирует с текущей ошибкой прогноза.
II. Применительно к процессам типа GARCH различные определения стационарности не согласованы. Строго стационарный GARCH процесс не всегда слабо стационарен. Различие между строгой и слабой стационарностью несущественно для линейных моделей: традиционно проверяемый набор условий является необходимым и достаточным как для ковариантной, так и строгой стационарности. Некоторые утверждения, устанавливающие ту или иную форму стационарности GARCH и EGARCH процессов, обсуждаются далее в параграфе 3.
|
|
|
III. Наконец, ограничения области допустимых значений параметров a и b создают трудности при оценивании GARCH модели.
В экспоненциальной модели (exponential GARCH, EGARCH), предложенной Д.Нельсоном (Nelson, 1991), логарифм условной дисперсии определяется с помощью некоторой функции g (×) стандартизованных ошибок:
(1.9)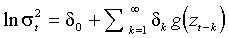 
Описанные выше эффекты учтены через данную функцию, которая зависит как от абсолютной величины, так и знака z:
(1.10)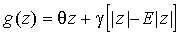 
.
Процесс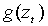 
имеет нулевое условное математическое ожидание, поэтому логарифм условной дисперсии является процессом линейной фильтрации. Соотношением (1.9) 
представлен как скользящее среднее бесконечной степени, однако для практических целейприменяется ARMA (p, q) репрезентация:
(1.11)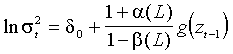 
.
Запись (1.11) корректна, если полиномы 1+a (x) и 1-b (x) не имеют общих корней. Никаких ограничений на параметры, связанных с требованием неотрицательности условной дисперсии, в (1.9)-(1.11) не налагается.
Оба слагаемых 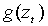имеют нулевое среднее; если распределение z симметрично, они ортогональны. В интервале 
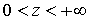g (z)линейна по z с коэффициентом наклона q + g; в интервале 
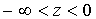g (z)линейна по z с коэффициентом наклона q - g. Таким образом, условная дисперсия реагирует асимметрично на неожиданные падения и подъемы рынка.
Член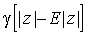 
представляет “эффект абсолютного значения” в духе GARCH моделей. Предположим, 
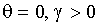. Тогда инновация логарифма условной дисперсии g (z) положительна (отрицательна), если абсолютное значение z больше (меньше) ожидаемого. Член q z ответственен за “эффект алгебраического знака”. Предположим, 
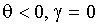. Инновация условной дисперсии положительна (отрицательна), если ошибка прогноза доходности отрицательна (положительна).
Если распределение z симметрично, то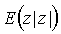 
равно нулю и
.
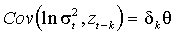Левередж-эффект имеет место, если q < 0. Гипотеза об отрицательной ковариации между и 
находит эмпирическое подтверждение в работах Nelson (1991) и Bollerslev, Engle и Nelson (1993), отдельные результаты которых более подробно обсуждаются в следующих разделах.
ДРУГИЕ ОДНОМЕРНЫЕ ПАРАМЕТРИЗАЦИИ.
Одним из представлений условной дисперсии GARCH процесса служит распределенный лаг квадратов остатков. Бесчисленные модификации базовой модели были получены применением различных функциональных форм для h (×) в рамках более общего представления:
.
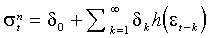Так, Higgins и Bera (1992) определяют класс нелинейных ARCH процессов (Non-linear ARCH), для которых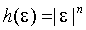 
.
|
|
|
Если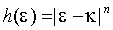 
, то условная дисперсия асимметрично реагирует на ошибки разных знаков; в частности, при k >0 возникает левередж-эффект, однако в отличие от EGARCH спецификации, инновации 
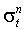всегда неотрицательны. Возможная модификация, соответствующая n =2: 
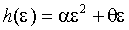. Другая параметризация, допускающая эффекты асимметрии:
(1.12)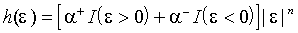 
,
где I (×) обозначает индикаторную функцию. Такая параметризация допускает неодинаковую чувствительность условной дисперсии к ошибкам разных знаков, однако утверждает, что минимум волатильности достигается при отсутствии ошибок.
Bollerslev, Engle и Nelson (1993) отмечают два недостатка параметризации EGARCH (1.9)-(1.10). I. Условные по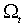 
вариация 
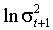и ковариация 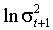и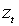 
постоянны. Желательно, чтобы оба момента могли изменяться в зависимости от 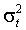. II. Условная дисперсия излишне чувствительна к выбросам. Авторы предлагают модификацию базовой модели
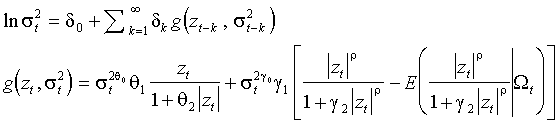
Параметры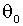 
и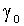 
отвечают первому требованию, 
, 
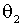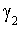и r регулируют уровень чувствительности условной дисперсии к инновациям в зависимости от их абсолютного значения. Положительные 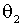и 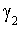приписывают хвостовым реализации 
относительно небольшой вес.
ARCH-M
Зависимость между ожидаемой отдачей и риском - центральный аспект финансовой теории. Традиционная модель ценообразования для капитальных активов (Capital Asset Pricing Model) и ее динамическая модификация Р. Мертона, арбитражная теория ценообразования С. Росса указывают на пропорциональную зависимость между ожидаемой избыточной отдачей рыночного портфеля и его условной дисперсией. ARCH-M, или ARCH in Mean модель является естественным инструментом для изучения этой проблемы в динамическом контексте, когда отдача и условная дисперсия развиваются во времени.
Модель типа ARCH-M предполагает явную функциональную зависимость условного среднего случайной величины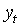 
от собственной условной дисперсии. Отвлекаясь от прочих регрессоров, возможно, участвующих в уравнении для условного среднего, можно записать
(1.13)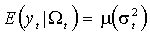 
.
Как правило, используется линейная от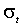 
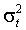, , или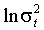 
форма функциональной зависимости, например 
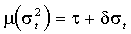, которая допускает следующую интерпретацию. Ожидаемая отдача рыночного портфеля распадается на две компоненты: безрисковый доход t и премию за риск 
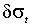. Экономические агенты ожидают увеличения доходности в связи с нарастанием неопределенности, коэффициент чувствительности ожидаемой доходности к изменениям условного стандартного отклонения связан с мерой относительного неприятия риска (relative risk aversion) и предполагается положительным.
Феномен положительной связи между условным средним и условной дисперсией может быть проиллюстрирован наблюдениями за доходностью ГКО в период январь 97 – август 98. Очевидно синхронное развитие условных моментов: наименьший уровень доходности зафиксирован в интервале июнь - сентябрь 97 года, этот же период характеризуется наименьшей турбулентностью, после чего увеличение доходности сопровождается видимым ростом волатильности.
Многочисленные примеры применения ARCH-M модели к отдаче вложений в различные фондовые индексы приводят к неоднозначным результатам. French, Schwert и Stambaugh (1987) для ежедневного индекса S&P, Chou (1988) для еженедельного NYSE, другие авторы для индексов США и Великобритании обнаружили положительную зависимость между отдачей и риском: полученные в этих работах оценки коэффициентов неприятия риска положительны и значимо отличаются от нуля. Напротив, Glosten, Jagannathan и Runkle (1991), Nelson (1991), Bollerslev, Engle и Nelson (1993) указывают на отсутствие такой зависимости, причем оцененный коэффициент неприятия риска в работе Nelson (1991) оказался отрицательным. Кроме того, некоторые регрессоры, например, лаги зависимой переменной, остаются значимыми в присутствии ARCH-M эффекта, величина и даже знак которого чувствительны к выбору инструментов, включаемых в уравнение среднего или дисперсии.
В связи с моделированием фондовых индексов особый интерес представляют работы Nelson (1991), Bollerslev, Engle и Nelson (1993). Нельсон моделирует отдачу вложений в средневзвешенный индексCRSP за период 1962-1987. Исследованием Боллерслева и др. охвачена динамика фондовых индексов США на протяжении более чем столетнего периода: Dow Jones за два отдельных периода 1985-1914 и 1914-28, Standard 90 (1928-52), S&P (1953-90).
В обеих работах применяются EGARCH модели. По критерию Schwartz для логарифма условной дисперсии четырех временных рядов выбрана ARMA (2,1) репрезентация, исключением стал DJ (1914-28), для которого выбрана AR (1) репрезентация. Все пять оцененных моделей свидетельствуют о левередж-эффекте (в обозначениях (1.10) q < 0, g > 0).
Функции условного среднего параметризованы как
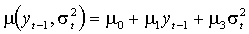(Nelson)
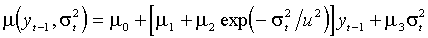(Bollerslev).
Обе параметризации отвергают наличие связи между уровнем доходности и ее волатильностью за единственным исключением. t -статистики коэффициента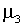 
составляют
| -1,6588 | для избыточной доходности вложений в CRSP (1962-1987) |
| -0,9826 | для дохода от увеличения рыночной стоимости CRSP (1962-1987) |
| 0,0287 | для DJ (1985-1914) |
| 0,7149 | для DJ (1914-1928) |
| 2,7941 | для Standard 90 (1928-1952) |
| 0,2347 | для S&P (1953-1990). |
Подтверждение получила гипотеза об отрицательной зависимости между серийной корреляцией и волатильностью, возможность которой учтена при помощи множителя в квадратных скобках (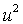
обозначает выборочную безусловную дисперсию 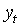): для DJ (1985-1914 и 1914-28), Standard 90 и для S&P параметр 
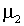положителен и значимо отличается от нуля. Для Standard 90, например, оцененная условная корреляция составляет 0.17, если 
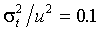и -0.07, если 
.
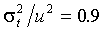ARCH-M модель привлекалась также для идентификации премии за риск во временной структуре процентных ставок и в связи с гипотезой эффективности валютного рынка.
Под временной структурой процентных ставок понимается соотношение между доходностью ценных бумаг с различными сроками погашения. Такая структура может быть проиллюстрирована в виде кривой дохода и демонстрирует меньший доход для краткосрочных ценных бумаг и больший - для долгосрочных. Рост ставок при движении от кратко- к долгосрочным бумагам можно объяснить возрастающим риском инвестирования. Engle, Lilien, Robins (1987) моделируют разницу в доходности 6-ти и 3-х месячных казначейских векселей (используются поквартальные данные за период 1960-1984, применяется ARCH (12) спецификация условной дисперсии). Динамика сверх доходности относительно более длинных бумаг (excess holding yield) обнаружила значимую компоненту, связанную с изменением условной дисперсии; однако, среднее значение этой компоненты составляет лишь 0.14 процента за квартал.
Гипотеза эффективности валютного рынка утверждает, что форвардный валютный курс является лучшим несмещенным прогнозом будущего курса наличной валюты. Однако практические наблюдения вселяют сомнения относительно эффективности валютного рынка в этом смысле. Смещенность форвардного курса не обязательно свидетельствует о нерациональности участников рынка и может быть манифестацией премии за риск. Эмпирически тестировались различные аппроксимации премии за риск, в том числе связанные непосредственно с условной дисперсией курса спот (Domowitz и Hakkio (1985); Kendall и McDonald (1989)); эти работы приводят к противоречивым результатам относительно адекватности ARCH-M спецификации.
1.2 СТАЦИОНАРНОСТЬ.
В данном параграфе мы обратимся к некоторым утверждениям, устанавливающим ту или иную форму стационарности GARCH и EGARCH процессов. Строгая форма стационарности предполагает, что все вероятностные характеристики процесса 
не меняются с течением времени; в частности, безусловное распределение вероятностей при всех t является одним и тем же. При слабой (ковариантной) форме стационарности безусловная дисперсия ограничена и совпадает для всех t.
Вернемся к определению параграфа 1.1 и рассмотрим ARCH-N – процесс, т.е. такой, условное распределение которого является нормальным:
(2.1)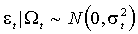 
.
Соответствующий стандартизованный процесс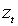 
имеет условно нормальное распределение с параметрами 0 и 1: 
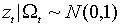. Поскольку нормальная плотность определяется лишь двумя своими параметрами, плотность распределения 
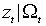неизменна при всевозможных значениях 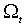. Следовательно, 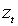независимы от входящих в набор 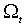случайных величин и любых функций от этих случайных величин. В частности, 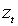не зависит от 
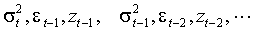. Это наблюдение позволяет сформулировать эквивалентное (2.1) определение ARCH-N процесса:
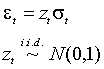
В общем случае (без предположения об условной нормальности) свойство одинаковой распределенности и независимости стандартизованных остатков не является следствием определения, данного в параграфе 1. Однако это свойство упрощает изучение вопросов данного параграфа. Поэтому мы усилим определение ARCH процесса:
ОПРЕДЕЛЕНИЕ
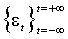является ARCH процессом, если
(2.2.а)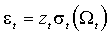 
(2.2.б)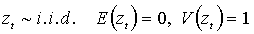 
.
GARCH
Теорема 1 описывает множество таких значений параметров a и b, при которых GARCH (1,1) является стационарным в строгом смысле.
Теорема 1 (Nelson, 1990).
Пусть процессы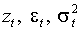 
определены (2.2) и (1.5), причем p= 1, q =1, w >0. Процесс строго стационарен если и только если
(2.3)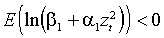 
.
Условие ковариантной стационарности для GARCH (p, q) установлено теоремой 2. Свойство ограниченности безусловной дисперсии представляется желательным из соображений экономического порядка, однако для реальных процессов является скорее исключением, чем правилом.
Теорема 2 (Bollerslev, 1986).
Пусть процессы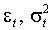 
определены (1.1) и (1.5). Процесс ковариантно стационарен если и только если все корни 1-b (x)-a (x)=0 лежат вне единичного круга. Безусловная дисперсия равна
.
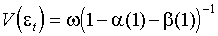Условие теоремы очевидно в свете представления (1.7). Для GARCH (1, 1) критерий ковариантной стационарности сводится к
(2.4)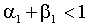 
.
Применением неравенства Иенсена в (2.3) можно установить, что слабая форма стационарности является достаточным, но не является необходимым условием для строгой формы стационарности. Например, процессы, для которых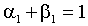 
, или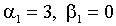 
являются строго стационарными, однако безусловная дисперсия этих процессов бесконечна.
Указания на ковариантную нестационарность высокочастотных временных рядов объединяют большую часть эмпирической литературы. О возможной ковариантной нестационарности говорит близость оцененного значения a (1)+b (1) к единице. Формальные тесты на единичный корень в дисперсии представлены рядом авторов, включая French, Schwert и Stambaugh (1987) для индекса S&P, Chou (1988) для средневзвешенного NYSE; нулевая гипотеза не была отвергнута ни в этих, ни во многих других работах.
Engle и Bollerslev (1986) определяют процессы с единичным корнем в дисперсии как интегрированные GARCH (Integrated GARCH, IGARCH), например, для IGARCH (1,1)
.
IGARCH процессы строго стационарны, однако не имеют ограниченной безусловной дисперсии. Прогноз волатильности на s шагов вперед определен как
,
так что текущая информация остается значимой, каков бы ни был горизонт прогнозирования.
Определенный интерес представляет четвертый безусловный момент: согласно многочисленным свидетельствам, распределения цен / доходностей различных финансовых активов имеют положительный куртозис. Это наблюдение столь распространено в литературе, что Bollerslev, Engle и Nelson (1993) относят его к эмпирически установленным закономерностям (необходимые ссылки представлены Bollerslev, Chou и Kroner (1992)). Пусть ARCH-N процесс (2.1) имеет конечный безусловный момент четвертого порядка. Тогда, поскольку 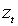и 
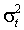независимы, и в силу неравенства Иенсена
,
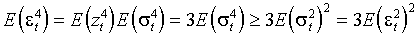причем равенство выполняется, лишь если 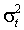– константа, т.е. условная гетероскедастичность не имеет места. В противном случае безусловное распределение характеризуется положительным куртозисом. Для GARCH (1,1)- N безусловный куртозис
,
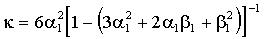если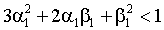 
и k = + ¥, иначе. В обоих случаях условная гетероскедастичность является источником безусловного избыточного куртозиса.
EGARCH
В экспоненциальной модели логарифм условной дисперсии является линейным процессом, поэтому свойства стационарности (как строгой, так и ковариантной) и эргодичности могут быть проверены сравнительно легко. Если шоки 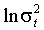угасают достаточно быстро, то логарифм условной дисперсии, условная дисперсия и сам ARCH процесс являются строго стационарными и эргодическими.
Теорема 3 (Nelson, 1991).
Пусть процессы 
определены (2.2) и (1.9)-(1.10), положим, g и q не равны нулю одновременно. Тогда процессы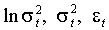 
строго стационарны и эргодичны, и ковариантно стационарен если и только если
.
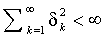Критерий теоремы 3 является традиционным для линейных процессов. Если логарифм условной дисперсии задан в форме авторегрессии – скользящего среднего соотношением (1.11), то условие теоремы сводится к требованию, чтобы все корни 1-b (x) лежат вне единичного круга. Так, например, если в (1.11) присутствует единственная авторегрессионная компонента (p =1), то критерий состоит в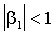 
.
Будучи строго стационарными, изучаемые процессы могут не иметь конечных безусловных моментов и, следовательно, не быть слабо стационарными. Это, в частности, так, если 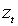имеет распределение Стьюдента. Если же распределение 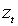принадлежит семейству GED (Generalized Error Distribution - Обобщенное Распределение Ошибки), то при условии строгой стационарности безусловное распределение обладает конечными моментами произвольного порядка.
Семейство GED охватывает симметричные распределения с различными коэффициентами куртозисами. Плотность распределения GED
(2.5)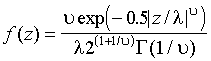 
где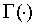 
- гамма-функция, и
.
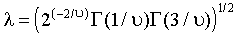параметризована u, регулирующим “толщину хвоста”. При u =2 GED совпадает со стандартным нормальным распределением, при u <2 плотность GED имеет более толстые, при u >2 – более тонкие хвосты, чем нормальная плотность. В частности, при u =1 z имеет двойное экспоненциальное распределение, при u = ¥ z равномерно распределен на интервале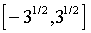 
.
Теорема 4 (Nelson, 1991).
Пусть процессы определены (2.2) и (1.9)-(1.10), положим, g и q не равны нулю одновременно, кроме того, 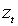имеют распределение GED с параметром u > 1. Пусть выполнено требование теоремы 3. Тогда процессы 
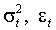обладают конечными, неизменными во времени моментами любого порядка.
Свидетельства нестационарности основных фондовых индексов США были получены в работах Nelson (1991), Bollerslev, et al (1993) применением EGARCH параметризации. Авторы указывают, что один из оцененных авторегрессионных корней ARMA(2,1) модели для логарифма условной дисперсии близок к единице, тогда как другой корень имеет невысокое абсолютное значение.
ГЛАВА 2. МЕТОДЫ ОЦЕНИВАНИЯ.
СПЕЦИФИКАЦИЯ МОДЕЛИ.
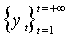– последовательность наблюдаемых скалярных случайных величин. 
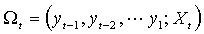- набор предопределенных к моменту t переменных. Функции условных мат. ожидания и дисперсии 
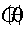совместно параметризованы вектором 
: 
. 
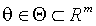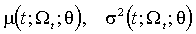– известные функции, которые далее будем обозначать, опуская аргумент 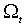и используя нижний индекс t. Существует единственный 
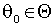такой, что
(М. 1)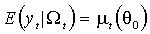 
(М. 2)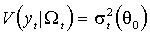 
,
называется вектором истинных параметров. Определим также функции остатков и стандартизованных остатков
.
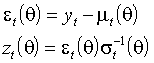Условия (М. 1)-(М. 2) позволяют вычислить математическое ожидание и дисперсию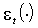 
в произвольной точке параметрического пространства. Например, в точке
(М. 3)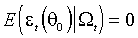 
(М. 4)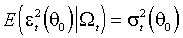 
.
Процедура, используемая наиболее часто для оценки , состоит в максимизации функции правдоподобия, построенной в предположении о том, что распределение 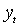при условии 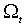нормально со средним и дисперсией, определенными (М. 1)-(М. 2). Гипотеза об условной нормальности, однако, часто не выдерживает тестирования; в этой связи возникает проблема выбора метода, устойчивого к различным ее нарушениям.
Обоснован метод квази-максимального правдоподобия, который предполагает максимизацию нормальной функции правдоподобия при том, что распределение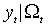 
в действительности не является нормальным. При этом оценки сохраняют свойства состоятельности и асимптотической нормальности, однако утрачивают свойство асимптотической эффективности.
В данной работе предпринята попытка оценить модель обобщенным методом моментов. Оказалось возможным построить оптимальные инструменты, приводящие к оценкам, асимптотически более эффективным, чем оценки метода квази-максимального правдоподобия.
|
|
|
