 |
Нарушения гипотезы об условной нормальности: метод квази-максимального правдоподобия.
|
|
|
|
Гипотезу (N) позволяет протестировать верное в нуле свойство независимости и нормальной распределенности стандартизованных остатков. Как правило, гипотеза отклоняется из-за того, что оцененные 
демонстрируют положительный куртозис. Реже причиной отклонения нулевой гипотезы становится асимметрия (необходимые ссылки представлены Bollerslev, Chou и Kroner (1992)).
Рядом авторов реализован ММП в предположении о том, что плотность распределения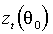 
принадлежит некоторому параметризованному семейству ¦(z,u). Так, Bollerslev (1987), Nelson (1990), Bollerslev, Engle и Nelson (1993) применяют, соответственно, t -Стьюдента, GED, и обобщенное t -Стьюдента распределения. Плотности t и GED имеют единственный параметр, регулирующий величину куртозиса, плотность обобщенного t -распределения имеет два параметра и включает t и GED как частные случаи (свойства GED обсуждались в параграфе 2). Параметры u и q оцениваются одновременно максимизацией логарифмической функции правдоподобия
.
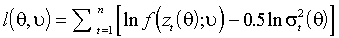С точки зрения асимптотической эффективности ММП с корректно определенной функцией плотности ¦ (×,×) является наилучшим решением. Реализация его, однако, технически крайне трудна: поскольку производные соответствующих функций правдоподобия не могут быть представлены аналитически, для максимизации их прибегают к методам численного дифференцирования.
Качество подбора функции плотности ¦ (×,×) можно установить, сравнивая фактическое и ожидаемое количества таких значений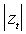 
, которые превосходят некоторое заданное Z. В этом смысле GED не вполне адекватно отражает частоту “хвостовых событий”: фактическое число выбросов гораздо больше, чем если бы 
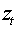были реализациями GED -распределенной случайной величины со значением параметра u, равным оцененному. Кроме того, t и GED симметричны, тогда как асимметрия – одна из важных особенностей изучаемых в данной работе российских финансовых активов. По этим причинам ММП был предпочтен методам квази-максимального правдоподобия и моментов. Среди других распределений, примененных при оценивании ARCH модели, – смесь нормального и логнормального, нормального и Пуассона распределений.
|
|
|
Установлено, что максимизация критериальной функции (3.1)-(3.2) приводит к состоятельным и асимптотически нормальным оценкам независимо от того, как именно распределены случайные величины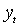 
. В тех случаях, когда истинное распределение 
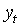неизвестно, эту процедуру принято называть методом квази- (псевдо-) максимального правдоподобия (МКМП). Отличие ее от традиционного ММПсостоит в матрице ковариации оценок:
(3.17) 
.
Равенство 
неверно в общем случае без предположения об условной нормальности, поэтому (3.17) не эквивалентно (3.13). МКМПнеизбежно приводит к потере асимптотической эффективности. Потери эффективности, возникающие, в частности, при t -распределенных ошибках невелики, однако могут быть весьма существенными, если распределение ошибок асимметрично.
Для вывода равенств (3.5), (3.6), (3.8), и (3.10) предположение (N) не привлекалось, все они являются следствием верной спецификации функций условного среднего и дисперсии, т.е. (M. 1)-(M. 2). Поэтому матрица 
остается состоятельной для гессиана, 
– состоятельной для информационной матрицы. Однако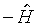 
и не являются асимптотически эквивалентными, как не являются асимптотически эквивалентными минус гессиан и информационная матрица. Оценкой ковариацонной матрицы КМП-оценок служит
(3.18)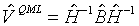 
.
Оценка (3.18) устойчива к нарушению гипотезы об условной нормальности в том смысле, что остается состоятельной для ковариации оценок, полученных максимизацией (3.1)-(3.2). Оценки 
и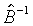 
при указанном нарушении свойства состоятельности не сохраняют.
|
|
|
ТЕСТИРОВАНИЕ
Асимптотическая нормальность оценок КМП позволяет воспользоваться стандартными процедурами. Пусть нулевая гипотеза формулируется как
(3.19)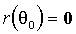 
,
где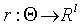 
дифференцируема на 
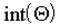и l<m. Если 
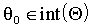и матрица 
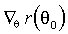имеет ранг l, то применима статистика Вальда
(3.20)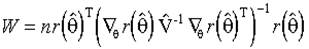 
,
где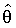 
- оценки параметров при альтернативной гипотезе (оценки полной модели, без ограничений (3.19)), 
- состоятельная оценка ковариации 
. При верной гипотезе (N) следует использовать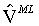 
, в противном случае - 
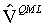. Верно предположение (N) или нет, в нуле статистика Вальда имеет асимптотическое хи-квадрат распределение с m-l степенями свободы. Тест Вальда
(3.21)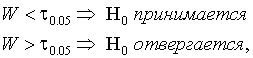 
где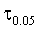 
- 5%-й квантиль 
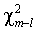распределения, характеризуется асимптотической ошибкой первого рода 5%: вероятность отвергнуть 
тогда как она верна
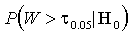
при увеличении числа наблюдений сходится к
.
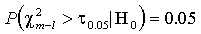Асимптотические результаты могут оказаться неприемлемыми для малых выборок и при некорректном выборе матрицы . Bollerslev и Wooldridge (1992) сообщают результаты имитационных экспериментов, проливающих свет на характер искажений, связанных с использованием в тестировании несостоятельных оценок 
при нарушении гипотезы (N). Общий вывод исследования состоит в следующем: ковариационные матрицы систематически недооценивают истинные размеры стандартных ошибок.
Схема исследования такова. Построены 1000 реализаций AR (1)- GARCH (1,1) процесса, имеющего условное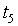 
распределение. Для каждой реализации вычислены
- оценки параметров истинной модели;
- ковариационные матрицы оценок трех типов:
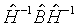, , . Эти типы будем вслед за авторами называть соответственно RB (от robust - устойчивый), HE (от hessian - гессиан), OPG (от outer product of the gradient - внешнее произведение градиента). - статистики Вальда для верной нулевой гипотезы
(3.19) трех типов по общей формуле (3.20). Тип статистики определяется типом оценки вариационной матрицы, применяемой в (3.20) - RB, HE, или OPG.
Имитационные эксперименты позволяют построить эмпирические распределения трех вариантов статистики Вальда при верной нулевой гипотезе, которые затем сопоставляются с хи-квадрат распределением. Полученные распределения имеют более толстые хвосты, чем 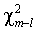. Так, например, доля реализаций статистики Вальда типов HE и OPG, лежащих правее 5%-го квантиля 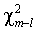, больше 0.05, скажем, 0.1. Это означает, что тест(3.18) имеет ошибку первого рода 10%, а не 5%. Иными словами, вероятность отвергнуть нулевую гипотезу в то время как она верна составляет 0.1:
|
|
|
.
Распределение RB -статистики близко к 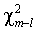. Использование устойчивой формы статистики Вальда, как и следовало ожидать, предпочтительнее двух других, причем OPG -статистика наименее точна. Таким образом, как , так и 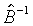систематически преуменьшают вариацию оценок и вводят в заблуждение относительно того уровня значимости, с которым нуль может быть отвергнут.
Точность всех форм статистик снижается при переходе к несимметричному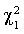 
распределению 
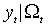. Аналогичные результаты были получены и для LM статистики.
ЧИСЛЕННЫЕ МЕТОДЫ НАХОЖДЕНИЯ ОЦЕНОК
Значения, доставляющие максимум критериальной функции (с соответствующими оговорками), удовлетворяют условиям первого порядка
(3.22) 
.
Нахождение численного решения системы (3.22) предполагает реализацию алгоритма, i -й шаг которого задается формулой
(3.23)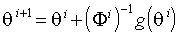 
.
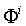- некоторая симметричная, положительно определенная матрица размерности m´ m. В качестве 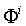могут быть использованы гессиан или оценка информационной матрицы, вычисленные на i -м шаге с использованием 
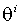. Стационарная точка последовательности 
удовлетворяет (3.22).
Для упрощения вычислений разработан прием, называемый искусственной регрессией (auxiliary regression): вектор приращений параметров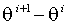 
приводится к характерному виду 
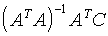при помощи некоторых искусственных переменных A и C.
Запишем в форме искусственной регрессии шаг алгоритма, использующего в качестве взвешивающей матрицы минус условный гессиан 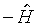. Воспользуемся матрицей регрессоров размерности 2n´ m и 2n -компонентным вектором зависимой переменной
, 
.
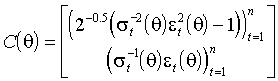Градиент и минус гессиан записываются через переменные A и C как
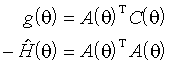
Шаг алгоритма приобретает вид
.
Запишем искусственную регрессию для алгоритма со взвешивающей матрицей вида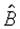 
. Независимые переменные данной регрессии формируют n´ m матрицу вкладов в градиент 
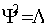со строками 
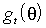. В качестве независимой переменной выступает n´ 1вектор i, все компоненты которого равны единице. Тогда
|
|
|
Шаг алгоритма приобретает вид
.
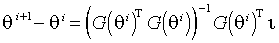Выбор матрицы F в (3.22) влияет на скорость сходимости алгоритма. С этой точки зрения рассмотренная выше форма HE взвешивающей матрицы предпочтительнее OPG. Для оптимизации скорости сходимости алгоритма можно корректировать длину вектора изменения параметров в заданном направлении с помощью дополнительного параметра l:
.
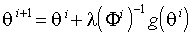Целесообразно выбирать l, максимизируя по нему критериальную функцию:
.
Использование l особенно полезно тогда, когда точка максимума критериальной функции лежит вблизи границы Q. В этих случаях промежуточные оценки, вычисляемые с помощью (3.23), могут оказаться вне Q, что приводит к остановке алгоритма.
ОБОБЩЕННЫЙ МЕТОД МОМЕНТОВ
Обобщенный метод моментов (ОMM)обладает следующими достоинствами:
- не требует явных предположений относительно плотности условного распределения и допускает присутствие ненулевых куртозиса и асимметрии;
- использует лишь производные первого порядка функци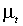й
и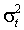 
и позволяет избежать тем самым применения методов численного дифференцирования; - асимптотически более эффективен, чем МКМП. Проверка метода на выборочных данных, демонстрирующих экстремально высокие коэффициенты асимметрии и куртозиса, свидетельствует о значительном выигрыше в эффективности.
Дополним модель (М. 1)-(М. 4) предположениями относительно третьего и четвертого моментов распределения :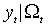
(М. 5)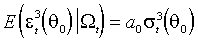 
(М. 6)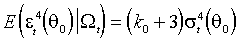 
,
где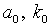 
- постоянные коэффициенты асимметрии и куртозиса. Стандартизованные остатки в точке 
тогда имеют первые четыре момента, равные соответственно 0, 1, 
. Гипотеза нормальности формулируется как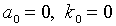 
.
Спецификация (М) обеспечивает две группы уравнений, идентифицирующих истинные значения параметров. Пусть
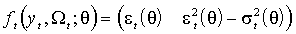
– строка из двух элементов, которую далее будем обозначать, опуская аргументы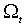 
и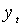 
. Мат. ожидания 
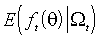существуют для всех q Î Q и обращаются в ноль единственным 
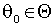. В этом смысле система уравнений
(3.19) 
идентифицирует истинный вектор параметров. Определим условные матрицу ковариации и якобиан 
в точке как
(3.20) 
(3.21) 
.
Класс оценок ОММ порождается различными наборами инструментальных переменных, выбор которых ограничен последовательностью 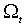. Асимптотическая ковариационная матрица ОММ оценок ограничена снизу, причем существует набор оптимальных инструментов, приводящий к эффективным оценкам.
Пусть l инструментов могут быть организованы в матрицу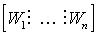 
размерности l´ 2 n, где 
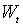- часть матрицы размерности l´ 2, относящаяся к наблюдению t (вклад данного наблюдения в матрицу инструментов). Требуется, чтобы число инструментов было не меньше числа оцениваемых параметров, т.е. l ³ m, и чтобы к моменту t значения 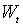были известны: 
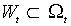; можно указать бесконечное число инструментальных переменных. Эмпирические моменты, соответствующие данному набору инструментов могут быть выражены как
|
|
|
(3.21) 
.
Матрица условной ковариации эмпирических моментов в точке равна
(3.22) 
.
Если l=m, то оценки 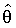находятся решением системы m уравнений
(3.23)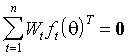 
,
если l>m, то минимизацией критериальной функции – квадратичной формы, построенной из (3.21) и (3.22):
(3.24) 
.
При любом выборе инструментов оценки, определяемые (3.23) или (3.24), состоятельны и асимптотически нормальны с асимптотической матрицей ковариации
(3.25)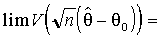 
.
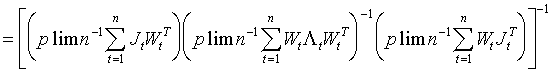Инструменты W, такие что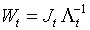 
, приводят к оценкам, эффективным в классе ОММ. Существует ровно m оптимальных инструментов, поэтому эффективные оценки находятся решением системы
(3.26)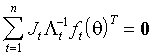 
.
Асимптотическая матрица ковариации таких оценок меньше, чем при любом ином выборе инструментов:
(3.27)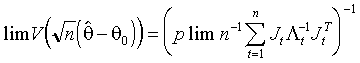 
.
Воспользуемся матрицами 
размерности l´ 2 n, 
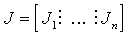размерности m´ 2 n, блочно-диагональной матрицей L размерности 2 n´ 2 n с диагональными блоками 
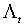. Тогда участвующие в (3.25) и (3.27) суммы записываются как 
, 
, 
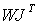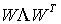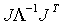. Опустим знаки p lim, множители 
и рассмотрим разность
между обращенными матрицами ковариации, относящимися к оптимальному и произвольному наборам инструментов, соответственно. Если симметричная 2 n´ 2 n матрица Y такова, что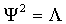 
, то разность данная равна
.
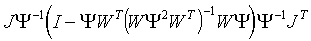Эта матрица положительно полуопределена, поскольку матрица в больших скобках идемпотентна. Отсюда немедленно следует положительная полуопределенность
.
Оптимальные в классе ОMM оценки асимптотически более эффективны, чем оценки МКМП. Достаточно показать, что асимптотическая матрица ковариации последних приводима к виду (3.25) с помощью какого-либо набора неоптимальных инструментов. Вклад наблюдения t в этот набор инструментов представляет собой матрицу 
, вычисленную при :
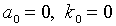(3.28)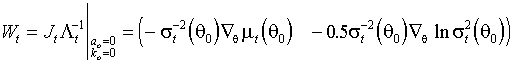 
.
Если коэффициенты асимметрии и куртозиса действительно равны нулю, то такой набор инструментов является оптимальным. Следовательно, при верной гипотезе (N) методы моментов и максимального правдоподобия асимптотически эквивалентны.
Выбор инструментов (3.28) приводит к следующим совпадениям:
- эмпирических моментов и градиента критериальной функции
(3.1)-(3.2)
в точке истинных параметров с точностью до знака “минус”: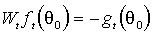 
;
- их условных ковариационных матриц:
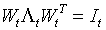, и
- условных вторых производных:
.
Следовательно, совпадают и вероятностные пределы, участвующие в (3.15) и (3.25). Итак, (3.25) при соответствующем выборе инструментальных переменных характеризует асимптотическую ковариационную матрицу МКМП -оценок.
Davidson и MacKinnon предлагают двухшаговую или итеративную процедуры вычисления оценок ОMM. Требуется построить состоятельные, но, возможно, неэффективные оценки, используя их, определить приблизительно оптимальные инструменты; с помощью найденных инструментов вычислить оценки параметров. Если исходные оценки не очень точны, желательно повторить процедуру несколько раз.
Пусть имеются , с помощью которых можно состоятельно оценить коэффициенты асимметрии и куртозиса выборочными моментами стандартизованных остатков:
(3.29)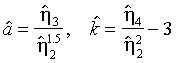 
.
Для всех q Î Q определим выражения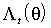 
и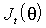 
, причем для вычисления первого из них вместо истинных значений 
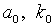будем использовать оценки (3.29). Новые оценки параметров q предлагается вычислять как решение системы
,
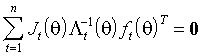где t -е слагаемое равно
(3.31) 
.
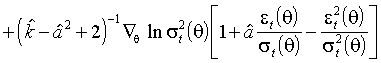При этом оценки оптимальных инструментов и оценки параметров определяются одновременно. Такое вычисление эквивалентно реализации итеративной процедуры, в которой оценки на i -м шаге 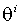определяются с помощью инструментов, оцененных на (i -1)-м шаге как решение
.
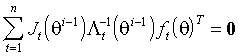Полученные оценки приводят к новым значениям коэффициентов асимметрии и куртозиса, и процедура может быть повторена. На практике уже после третьей итерации достигается вполне удовлетворительная сходимость.
В качестве исходных оценок приемлемы оценки максимального правдоподобия. При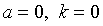 
вклад t-го наблюдения в эмпирический момент (3.31) совпадает со вкладом в градиент логарифмической функции правдоподобия. Следовательно, оценки максимального правдоподобия могут быть получены на первом шаге решением (3.30) при .
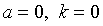Оценкой ковариационной матрицы для 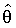служит
,
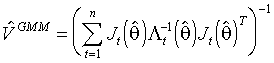где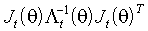 
=
.
|
|
|
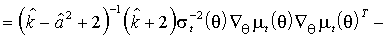
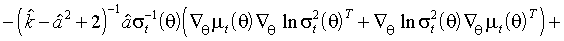
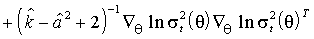