 |
Дифференциальные уравнения движения вязкой жидкости (уравнения Навье-Стокса)
|
|
|
|
До сих пор мы не рассматривали влияние сил вязкого трения на движение жидкости. Попытаемся учесть эти силы. Для простоты рассмотрим движение реальной (вязкой) жидкости в проекции на одну координату. Будем считать, что частица в форме параллелепипеда с размерами dx, dy, dz движется вдоль оси X. За счёт сил вязкого трения на верхнюю и нижнюю поверхности рассматриваемого объёма будут действовать силы трения dTв и dTн соответственно. Эти силы зависят от площади трения dydz и величины касательного напряжения на поверхностях трения τ. На нижней поверхности сила трения будет:
,
на верхней она будет отличаться на величину приращения касательных 
напряжение вдоль оси Z
.
Равнодействующая этих сил, действующая на рассматриваемый объём будет равна разности сил трения
,
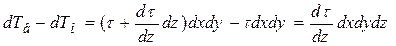или
,
где 
- величина рассматриваемого объёма жидкости.
Напряжение внутреннего трения, обусловленного вязкостью, по закону жидкостного трения имеет вид:
,
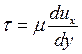где 
- динамический коэффициент вязкости.
После подстановки получим:
.
В уравнениях Эйлера все силы отнесены к единичной массе, поэтому и силы, обусловленные вязким трением, приведём к такому же виду:
,
где 
- кинематический коэффициент вязкости.
Если подобные рассуждения провести для остальных координат, т.е. перейти к общему случаю пространственного движения, когда составляющие скорости 
являются функциями трёх координат X, Y, Z. В таком случае проекция силы вязкого трения на ось X в пересчёте к единице массы даёт величину:
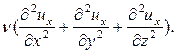
Аналогичные выражения можно записать для двух других координат. Если уравнения Эйлера для движущейся жидкости дополнить проекциями сил вязкого трения на оси координат, получатся дифференциальные уравнения движения вязкой жидкости, которые носят название уравнения Навье-Стокса и имеют следующий вид:
|
|
|
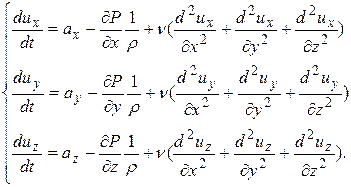
Лекция 10. Интегрирование уравнений Эйлера
Интегрирование уравнений Эйлера рассмотрим на широко распространённом примере движения жидкости под действием силы тяжести. Примерами такого движения могут служить: течение реки, ручья или любого другого потока жидкости, течение жидкости в водопроводе, работающем от водонапорной башни.
Движение жидкости описывается обобщённой формой уравнений Эйлера
.
В рассматриваемом случае, когда движение жидкости осуществляется исключительно под действием силы тяжести, силовая потенциальная функция
принимает вид:
,
где g – ускорение свободного падения.
Подставив это выражение в уравнение Эйлера, и умножив на «–1», для того, чтобы избавиться от знаков «минус» перед каждым слагаемым, получим:
После интегрирования придём к виду:
,
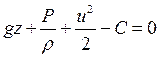где C – постоянная интегрирования (знак «-» перед ней не имеет
физического значения и поставлен только для удобства последующих математических преобразований).
Разделив последнее равенство на g, придём к окончательному виду:
.
Полученное выражение называется интегралом Бернулли, а постоянная величина H носит название гидродинамический напор или полный напор. Другое название интеграла Бернулли, которое применяется значительно чаще, - уравнение Бернулли для струйки идеальной жидкости.
Уравнение Бернулли
Выше уравнение Бернулли для струйки идеальной жидкости получено строгими математическими методами, использующимися в классической гидромеханике. То же уравнение можно получить (нестрого), используя рассуждения, которые часто применяются в гидравлике.
|
|
|
