 |
Основы теории подобия, геометрическое и динамическое подобие
|
|
|
|
Гидродинамическое подобие - это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.
Из геометрии известно, что геометрическое подобие означает пропорциональность сходственных размеров и равенство соответствующих угло 
в. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, Таким образом в гидравлике геометрическое подобие означает подобие русел или трубопроводов, по которым течёт жидкость.
Кинематическое подобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.
Динамическое подобие заключается в пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил.
В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.
На практике полное гидродинамическое подобие достигается редко, поэтому обычно приходится ограничиваться частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.
Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде
.
Критерии подобия для потоков несжимаемой жидкости
|
|
|
Критерий подобия Ньютона
В подобных потоках силы, с которыми поток воздействует на препятствия - твердые стенки, лопасти гидромашин, обтекаемые потоком тела, и другие преграды, должны быть пропорциональны. Этими силами являются силы инерции движущейся жидкости, которые пропорциональны произведению динамического давления 
на преграду при площади воздействия S.
Рассмотрим, как поток жидкости наталкивается на безграничную стенку, установленную нормально к нему, и в результате, растекаясь по ней, меняет свое направление на 90°. На основании теоремы механики о количестве движения секундный импульс силы 
, с которой поток действует на стенку, равен:
,
где 
- плотность жидкости,
- секундный расход жидкости,
- средняя скорость жидкости,
- площадь воздействия струи на преграду.
Это и есть сила воздействия на преграду. Для подобных потоков I и II должно выполняться равенство
,
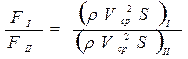или
.
Последнее отношение, одинаковое для подобных потоков, называется числом Ньютона и обозначается Ne.
Критерий подобия Эйлера
Вначале рассмотрим наиболее простой случай - напорное движение идеальной жидкости, т. е. такое движение, при котором отсутствуют силы вязкости. Для этого случая уравнение Бернулли для сечений 1-1 и 2-2 будет иметь вид:
.
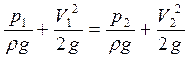Из условия неразрывности потока расходы в сечениях 1-1 и 2-2 с площадями соответственно 
и 
одинаковы, а это значит, что
,
откуда
.
Подставив последнее соотношение в уравнение Бернулли, после переноса членов получим:
.
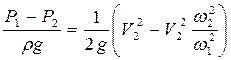После очевидных преобразований и сокращений придём к виду
.
Если два потока геометрически подобны, то правая часть уравнения имеет одно и то же значение, следовательно, левая часть тоже одинакова, т.е. разности давлений в сечениях 1-1 и 2-2 пропорциональны динамическим давлениям:
.
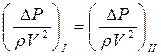Таким образом, при напорном движении идеальной несжимаемой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скоростной высоте), называется коэффициентом давления или числом Эйлера и обозначается Eu.
|
|
|
В случае напорного движения в приведённых уравнениях под 
можно понимать полное давление (на жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление, т. е. оно сводится лишь к соответствующему изменению давления за счёт глубины потока), т.к. при высоких давлениях величина давления, зависящая от глубины потока, несоизмеримо мала, и величина гидростатического напора практически полностью определяется избыточным давлением. Следовательно, для Eu можно записать:
,
где 
- разность статических напоров.
|
|
|
