 |
Течение при больших перепадах давления
|
|
|
|
В высоконапорных гидромашинах, например гидравлических прессах, может происходить ламинарное течение жидкости через малые зазоры при больших перепадах давлений порядка нескольких десятков и даже сотен мегапаскалей.
Опыт показывает, что в таких случаях падение напора вдоль потока оказывается существенно нелинейным, а закон Пуазейля дает заметную погрешность.
При таких течениях необходимо учитывать нагревание жидкости, которое ведёт к уменьшению её вязкости, причем степень влияния этого фактора будет нарастать вдоль потока жидкости. С другой стороны, с увеличением давления вязкость жидкостей возрастает. Таким образом, вязкость жидкости переменна вдоль потока и, как результат одновременного действия двух указанных факторов, продольный градиент давления 
, обусловленный трением, оказывается непостоянным.
Указанные факторы действуют и на расход: повышение температуры способствует его увеличению, а высокое давление в жидкости - его уменьшению, по сравнению со значением, определяемым законом Пуазейля. Таким образом, влияние этих двух факторов на расход является противоположным.
Рассмотрим задачу о ламинарном течении в зазоре толщиной а, длиной l и шириной b с учетом влияния на вязкость давления и температуры. При этом допускаем, что плотность жидкости не зависит от давления и температуры, а размеры зазора таковы, что его толщина существенно меньше ширины.
Ранее было установлено, что расход через плоскую щель составляет
Физическая сущность первого сомножителя в этом произведении – потери на трение по длине щели. Он показывает, как быстро теряется энергия по ходу течения жидкости. Причём потери на трение 
есть ни что иное, как уменьшение давления по длине щели l. Если учесть сказанное и перейти к пределу, эту величину можно характеризовать падением давления по длине зазора вида:
|
|
|
Знак «-» в этой формуле показывает, что давление по длине зазора уменьшается.
С учётом последнего и в пересчёте на единичную ширину зазора (b=1) расход через щель можно записать в виде
При рассмотрении свойств жидкости упоминались формулы, учитывающие изменение коэффициента динамической вязкости 
от температуры:
и давления:
Для одновременного учёта влияния на вязкость жидкости давления и температуры можно принять
.
В приведённых формулах, напомним, использованы следующие обозначения:
μt – динамический коэффициент вязкости при заданной температуре,
μP – динамический коэффициент вязкости при заданном давлении,
T0, P0, μ0 – температура, давление и динамический коэффициент вязкости жидкости в начале зазора,
T, P, μ – температура, давление и динамический коэффициент вязкости жидкости в конце зазора,
kt – коэффициент, для минеральных масел равный 0,02-0,03,
kP – коэффициент, для минеральных масел равный 0,002-0,003,
e – основание натурального логарифма, равное 2,718282.
Теперь запишем уравнение тепловой энергии, т. е. равенство между потерей энергии на трение, превратившейся в тепло, и приростом тепловой энергии жидкости за единицу времени:
,
где С - теплоемкость жидкости,
k — коэффициент, учитывающий долю работы сил вязкости, которая идет на нагревание жидкости.
При k = 1 теплоотдача в стенку отсутствует, и вся теряемая энергия, обусловленная вязким трением, идет на нагревание жидкости. При k = 0 происходит максимальная теплоотдача в стенку, в результате чего повышения температуры жидкости не происходит (изотермическое течение).
Из последнего равенства можно получить:
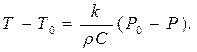
После подстановки этого равенства в выражение степени формулы для 
получим:
|
|
|
Произведём разделение переменных в уравнении расхода через зазор
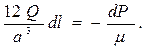
Используем полученную связь между μ и P выполним подстановку:
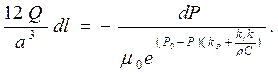
Произведём алгебраические преобразования: домножим обе части на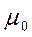 
и поменяем знак степени при e (
):
Проинтегрируем последнее выражение:
Результатом интегрирования, будет равенство:
Постоянную интегрирования С1 найдем, учитывая, что в начальном сечении потока при l= 0 P = Р0. Cледовательно:
Подставив постоянную интегрирования C1, получим
.
Выразим отсюда Q:
.
Приведённую формулу можно анализировать с различных позиций. Мы посмотрим на неё только с одной точки зрения. Сравним её с формулой расхода через щель, полученную на основании закона Пуазейля. Расход по закону Пуазейля линейно изменяется при изменении давления. Последняя же формула, учитывающая изменение вязкости при изменении давления и теплообмен в потоке, что имеет место, когда жидкость движется с большими скоростями и при больших перепадах давления, описывает связь давления и расхода степенной функцией. При этом чем выше давление, тем больше отклонение расхода от линейной зависимости, соответствующей закону Пуазейля. Объясняется это тем, что расход жидкости при ламинарном течении пропорционален перепаду давления ∆P, а величина потерянной энергии, равная произведению ∆PQ, пропорциональна квадрату перепада давления. По этой причине потеря энергии на единицу расхода жидкости растет пропорционально перепаду давления.
Список литературы
1. Башта Т.М. Гидравлика, гидравлические машины и гидравлические приводы.– М.: Машиностроение, 1970г.-504 с.
2. Башта Т.М. Машиностроительная гидравлика.- М.: Машиностроение, 1971г.-672 с.
3. Орлов Ю.М. Механика жидкости, гидравлические машины и основы гидропривода агрегатов ракетных комплексов. Учебное пособие. – М: ООО «Пресс-мастер», 2001.- 379с.
4. Иванов В.И., Навроцкий В.К., Сазанов И.И., Трифонов О.Н. Гидравлика и объемный гидропривод. Учебное пособие. - М.: ИЦ МГТУ «СТАНКИН», 2003. – 154 с.
5. Шейпак А.А. Гидравлика и гидропневмопривод: Учебное пособие. Ч1. Основы механики жидкости и газа. 2-е изд. Перераб. и доп. –М.: МГИУ, 2003. –192с.
6. Схиртладзе А.Г., Иванов В.И., Кареев В.Н. Гидравлические и пневматические системы.– М.: ИЦ МГТУ “Станкин”, Янус-К, 2003. –544с.
|
|
|
7. Станочные гидравлические системы. Под ред. Ф.Ю. Свитковского. – Ижевск-Екатеринбург, изд. Института экономики Ур. РАН., 2003. 239с.
8. Избаш С.В. Основы гидравлики. – М.: Государственное издательство литературы по строительству и архитектуре, 1952. 423с.
9. Чугаев Р.Р., Гидравлика: Учебник для вузов. – 4-е изд. доп. и перераб. - Л. Энергоиздат. Ленингр. отд-ние, 1982. 672с.
|
|
|
