 |
Прямое и обратное преобразования Лапласа
|
|
|
|
Прямое и обратное преобразования Лапласа
Прямое преобразование Лапсаса заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла

Для осуществления прямого преобразования Лапласа Maple 7 имеет функцию
laplace(expr,t,p)
Здесь ехрr— преобразуемое выражение, t — переменная, относительно которой записано ехрr, и р — переменная, относительно которой записывается результат преобразования.
Обратное преобразование Лапласа означает переход от функции F(p) к функции (t) с помощью формулы

Для вычисления этого интеграла служит функция:
invlaplace(expr,p, t)
где ехрr — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение а обратное —оригинал функции. Ниже приведены примеры применения прямого и обратного преобразований Лапласа:

Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t) + acos(t).
Gif

Gif

Gif

Прямое и обратное преобразования Фурье
Прямое и обратное преобразования Фурье
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот и заключается в вычислении следующей интегральной функции:

Оно реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr,t,w)
Здесь ехрr — выражение (уравнение или множество), t — переменная, от которой зависит ехрr, и w — переменная, относительно которой записывается результирующая функция. Обратное преобразование Фурье задается вычислением интеграла:
|
|
|

Оно фактически переводит представление сигнала из частотной области во временную. Примеры применения преобразования Фурье представлены ниже:
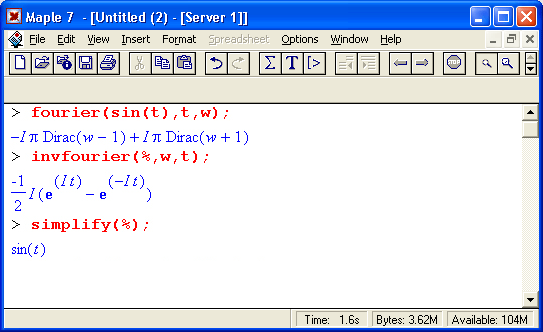
Обратите внимание на то, что даже в простом первом примере применение обратного преобразования Фурье вслед за прямым не привело к буквальному восстановлению исходной функции sin(t). Потребовалась: команда simplify, чтобы перевести результат в виде представления синуса через экспоненциальные функции к обычному виду sin(t).
Gif

Gif

Gif

Вычисление косинусного и синусного интегралов Фурье
Вычисление косинусного и синусного интегралов Фурье
Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:
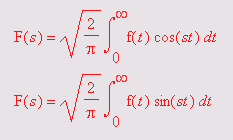
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция./(t). Для вычисления этих интегралов в пакете используются следующие функции:
fouriercos(expr,t,s)
fouriersln(expr,t,s)
Поскольку формат задания этих функций вполне очевиден, ограничимся примерами их применения:

Gif
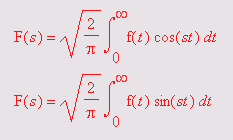
Gif

Интегральное преобразование Ханкеля
Интегральное преобразование Ханкеля
Интегральное преобразование Ханкеля задается следующим выражением:

и выполняется функцией:
hankel(expr, t, s, nu)
Здесь ехрr — выражение, равенство (или множество, или список с выражениями/равенствами), t — переменная в ехрr, преобразуемая в параметр преобразования s, nu— порядок преобразования. Следующий пример демонстрирует применение функции Ханкеля:

Gif

Gif

|
|
|


