 |
Прямое и обратное преобразования Гильберта
|
|
|
|
Прямое и обратное преобразования Гильберта
Прямое преобразование Гильберта задается следующим выражением:
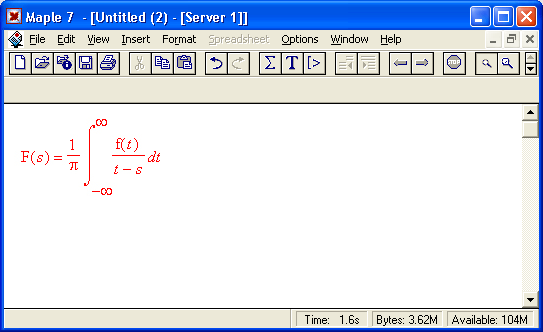
и превращает функцию f(t) в F(s).
Обратное преобразование Гильберта означает нахождение f(f) по заданной F(s).
Эти преобразования выполняются функциями:
hilbert(expr, t, s)
invhilbert(expr, t,s)
где назначение параметров очевидно.
Приведенные ниже примеры иллюстрируют выполнение этих преобразований:
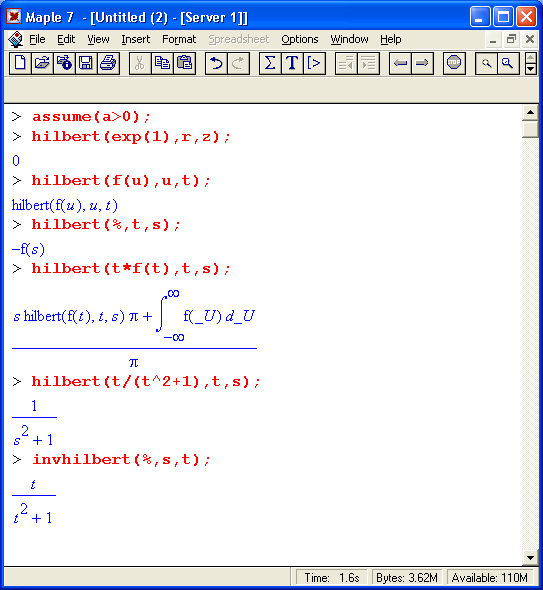
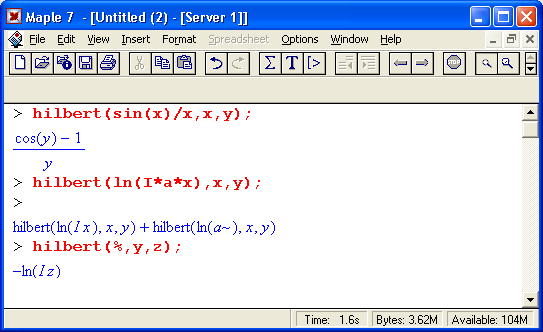
Как видно из этих примеров, обратное преобразование Гильберта, осуществленное над результатом прямого преобразования, не восстанавливает функцию f(t) буквально.
Gif

Gif

Gif

Интегральное преобразование Меллина
Интегральное преобразование Меллина
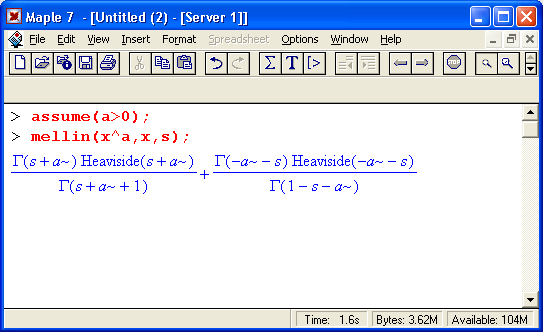
Интегральное преобразование Меллина задается выражением:

и реализуется функцией:
mellin(expr, х, s)
с очевидными параметрами ехрr, х и s.
Применение преобразования Меллина иллюстрируют следующие примеры:
Gif

Gif

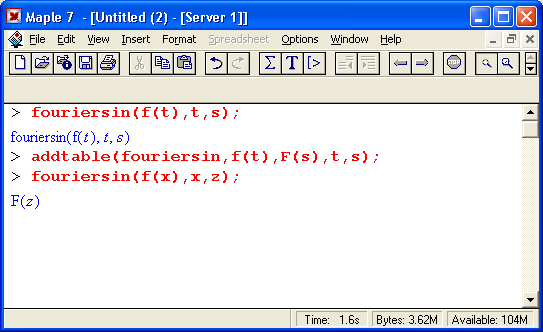
Функция addtable
Функция addtable
Как видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция:
addtable(tname,patt,ехрr,t,s)
где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны.
Следующие примеры поясняют применение этой функции:
Gif

Пакет приближения кривых CurveFittirrg
Пакет приближения кривых CurveFitting.
Общая характеристика пакета CurveFitting
Новый пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций:
> with(CurveFitting);
Доступ к функциям пакета возможен с помощью конструкций:
|
|
|
CurveFitting[function](arguments)
function(arguments)
Число функций пакета невелико и все они описаны ниже.
Функция вычисления В-сплайнов Bspline.
Функция вычисления В-сплайнов Bspline
Функция BSpline(k, v, opt) служит для вычисления В-сплайнов. Она имеет следующие параметры: k — порядок сплайна (целое число), v— имя и opt — параметр в виде knots=knotlist, где knotlist — спискок из k+1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve], можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже:

Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise.
Gif

Функция построения В-сплайновых кривых BsplineCurve
Функция построения В-сплайновых кривых BsplineCurve
Функция BsplineCurve служит для построения кривых в B-cплайнов. Она Может использоваться в формах:
BSpl1neCurve(xydata, v, opts)
BSpllneCurve (xdata, ydata, v, opts)
Здесь:
xydata — список, массив или матрица точек в форме [[xl.ylj, [х2,у2],..., [хn,уn]];
xdata — список, массив или вектор значений независимой переменной [xl,x2,...,хn];
ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,...,уn];
v — имя независимой переменной;
opts — необязательный параметр в форме одного или более выражений вида order=k или knots=knot1ist.
Примеры применения функции BSplineCurve с порядком, заданным по умолчанию, и с третьим порядком (кубический В-сплайн) представлены на рис. 14.6.
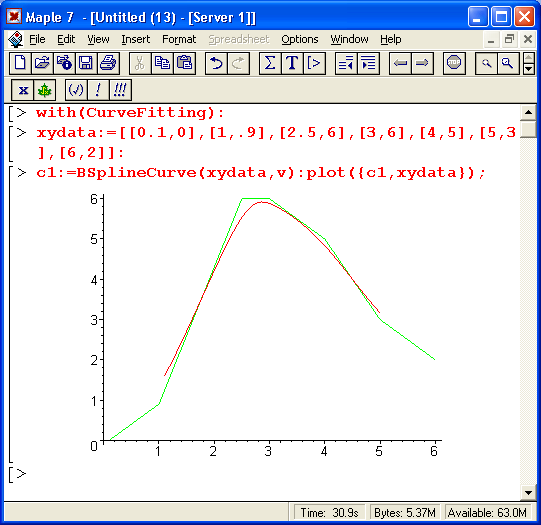
Рис. 14.6. Применение функции BSplineCurve
Следует отметить, что при малом, числе точек аппроксимация В-сплайнами дает невысокую точность, что и видно из рис. 14.6
Gif

|
|
|


