 |
Функция реализации метода наименьших квадратов LeastSquares
|
|
|
|
Функция реализации метода наименьших квадратов LeastSquares
Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов:
LeastSquares (xydata, v, opts)
LeastSquares(xdata, ydata, v.,opts)
Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset.
Следующие примеры иллюстрируют применение функции LeastSquares:

Gif

Функция полиномиальной аппроксимации Polynomiallnterpolation
Функция полиномиальной аппроксимации PolynomialInterpolation
Функция PolynomialInterpolation реализует полиномиальную интерполяцию и может использоваться в виде:
Polynomiallnterpolation (xydata, v)
Polynomiallnterpolation(xdata, ydata, v)
Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже:

Gif

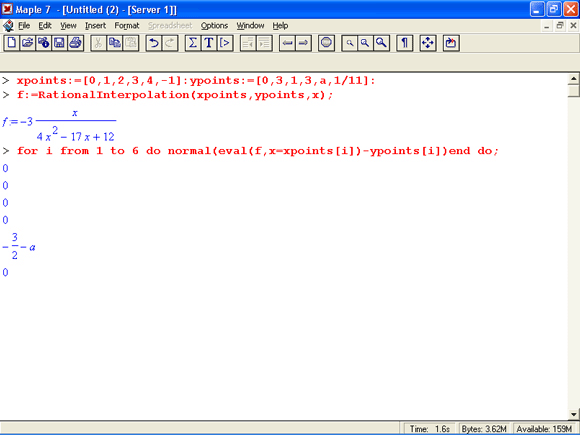
Функция рациональной аппроксимации Racionallnterpotation
Функция рациональной аппроксимации RacionalInterpolation
Функция рациональной интерполяции задается в Виде:
Rational Interpolation (xydata, z, opts)
RationalInterpolation(xdata, ydata, z, opts)
где необязательный параметр opts задается выражениями methochmethodtype или degrees=[dl,d2]. Функция возвращает результат в виде отношения двух полиномов. Параметр methodtype может иметь значения 4lookaround или subresultant, задающие учет или пропуск сингулярных точек.
Пример применения функции Rational Interpolation (загрузка пакета опущена, но предполагается):
Gif

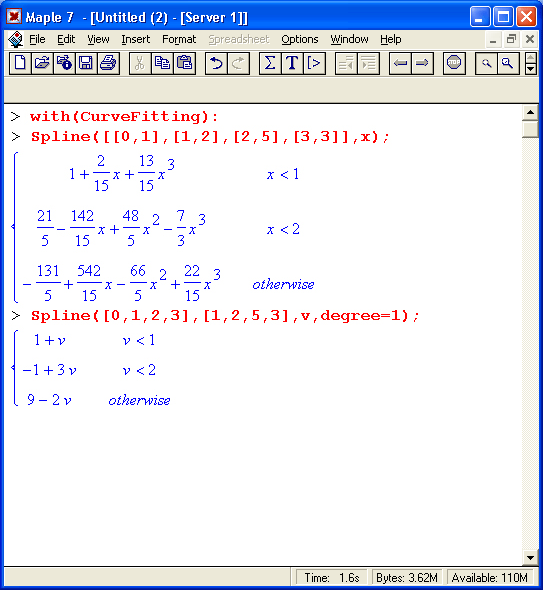
Функция вычисления обычных сплайнов Spline
Функция вычисления обычных сплайнов Spline
Функция:
Spline(xydata, v, opts)
Spline(xdata, ydata, v, opts)
вычисляет обычные (не В-типа) сплайны. Примеры ее применения даны ниже:
Gif

Функция аппроксимации непрерывными дробями Thielelnterpolation
Функция аппроксимации непрерывными дробями ThieleInterpolation
|
|
|
Функция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's-интерполяцию). Она задается в виде:
Thielelnterpolation (xydata, v)
Thielelnterpolation(xdata, ydata, v)
Примеры применения данной функции представлены ниже:

Gif

Пакет для работы с полиномами PolynomialTools
Пакет для работы с полиномами PolynomialTools
Обзор возможностей пакета PolynomialTools
Пакет для работы с полиномами PolynomialTools предназначен для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами. Этот пакет имеет небольшое число функций:
> with(PolynomialTools):
[IsSelfReciprocal, MinimalPolynomial, PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate]
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
Функции для работы с полиномами
Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера. Примеры применения этой функции представлены ниже:
ПРИМЕЧАНИЕ
Функция IsSelfReciprocat(a, х, 'р') проверяет полином а(х) на условие coeff(a,x,k) =coeff(a,x,d-k) для всех k = 0..d, где d = degree(a; х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином Р порядка d/2, такой, что x^(1/2)*P(x+l/x) = а. При нечетном d полином а будет взаимообратным, что подразумевает деление на х+1. В этом случае; если р указано, результат вычисляется в форме а/(х+1).
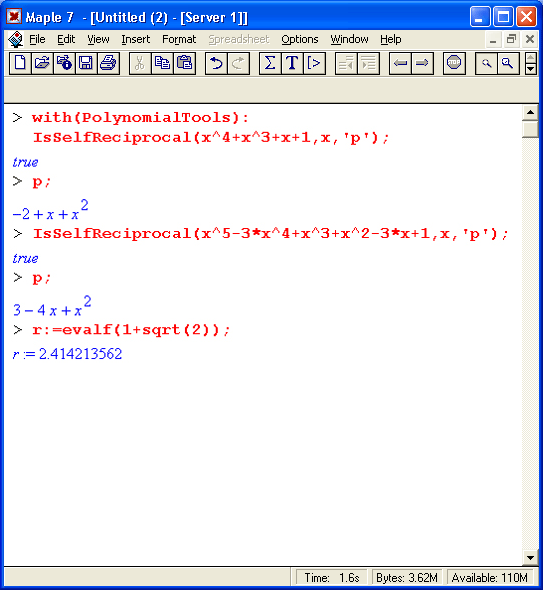
Функция MinimalPolynomial (r, n, асе) возвращает полином минимальной степени не превышающей n, имеющий корень г. Необязательный аргумент асе задает погрешность приближения. Функция MinimalPolynomia(r, n) использует решетчатый алгоритм и находит полином степени п (или менее) с наименьшими целыми коэффициентами. Корень г может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию асе задано как 10*(Digits-2). Примеры применения данной функции:
|
|
|
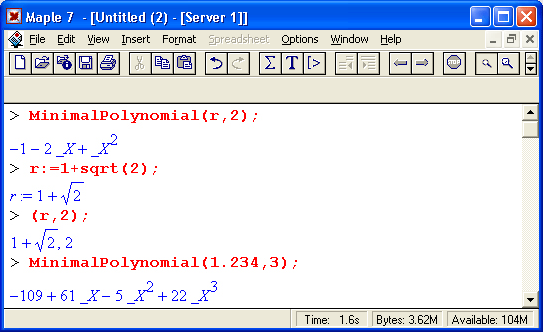
Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — необязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {tl,...,tm}, таких что полином а расщепляется над K=Q(tl,...,tm), где Q означает поле рациональных чисел. Примеры:

В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее.
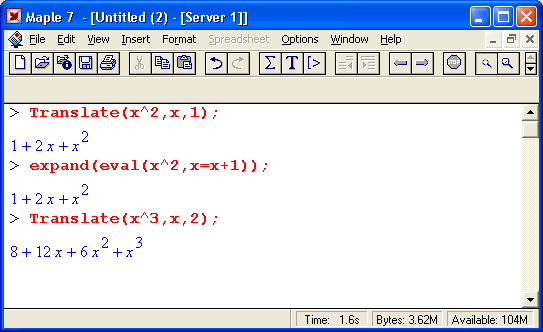
Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х - х + х0, где x0 — константа. Примеры применения этой функции даны ниже:
Gif

Gif

Gif

Gif

|
|
|


