 |
Пакеты линейной алгебры и функциональных систем
|
|
|
|
Основные определения линейной алгебры
Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple 7 по части решения задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.
Матрица (m х n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).
Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3x3:
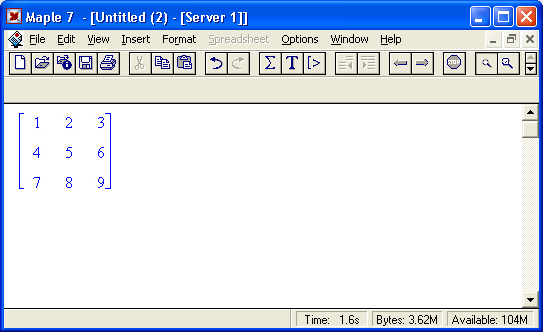
Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.
Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4x4:

Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы АТ=А, где Ат - транспонированная матрица А (см. ее определение ниже);Транспонированная матрица — матрица, у которой.столбцы и строки меняются. местами, то есть элементы транспонированной матрицы удовлетворяют условию AT(i,j)=A(j,i). Приведем простой пример. Исходная матрица:
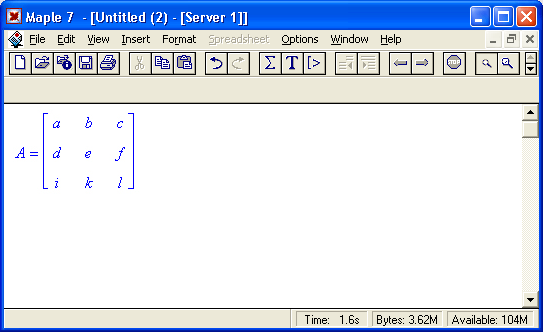
Транспонированная матрица:
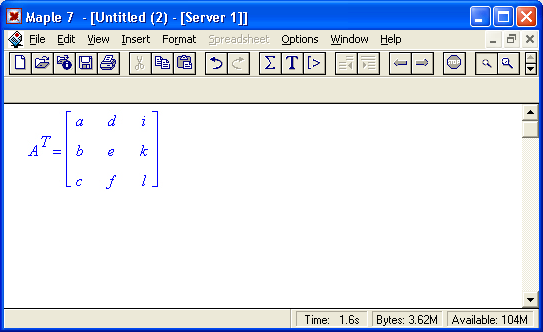
Обратная матрица — это матрица М-1, которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.
Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.
|
|
|
Диагональ матрицы — расположенные диагонально элементы Ai,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия под диагоналей (элементы d и k) и над диагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, под диагонали и над диагонали, равны нулю, называется ленточной.
Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.
След матрицы — сумма диагональных элементов матрицы.
Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

где M1<j> — определитель матрицы порядка n - 1, полученной из матрицы А вычеркиванием первой строки и j-гo столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.
Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом:
М° = Е, М1 = М, М2 = ММ..., Мn =Мn-1М.
Идемпотентная матрица — матрица, отвечающая условию Р2 = Р.
Симметрическая матрица — матрица, отвечающая условию Ат = А.
Кососимметрическая матрица — матрица, отвечающая условию Ат = -A. Ортогональная матрица — матрица, отвечающая условию Ат =А-1.Нуль-матрица — матрица, все элементы которой равны 0.Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.
|
|
|
Комплексно-сопряженная матрица — матрица А, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные. Эрмитова матрица — матрица А, удовлетворяющая условию А = А.Собственный вектор квадратной матрицы А — любой вектор х е V", х* О, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.
Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена, — |А - gE|. Собственные значения матрицы — корни ее характеристического многочлена. Норма — обобщенное понятие абсолютной (величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||).

Матричная форма записи системы линейных уравнений — выражение АХ = В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А-1В, где А-1 — обратная матрица.
Gif

Gif

Gif

Gif

Gif

Gif

|
|
|


