 |
6 Расчет вала концевой опоры. 6. 1 Расчет реакций в опорах. 6. 2 Расчет эпюры изгибающих моментов вала. 6. 3 Расчет вала на статическую прочность при действии пиковой нагрузки
|
|
|
|
6 РАСЧЕТ ВАЛА КОНЦЕВОЙ ОПОРЫ
6. 1 Расчет реакций в опорах

Рисунок 6. 1 - Расчетная схема нагружения вала
Для определения реакции в опоре B составляем уравнение суммы моментов относительно точки A и приравниваем его к нулю, т. к. конструкция находится в уравновешенном состоянии.
 ;
;
 ;
;
 ;
;
Подставляем численные значения известных элементов данного уравнения
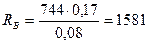 Н.
Н.
Для определения реакции в опоре A составляем уравнение суммы моментов относительно точки B и приравниваем его к нулю, т. к. конструкция находится в уравновешенном состоянии.
 ;
;
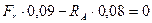 ;
;
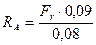 ;
;
Подставляем численные значения известных элементов данного уравнения
 Н.
Н.
6. 2 Расчет эпюры изгибающих моментов вала
На участке х1: M1=RA· x1;
x1 = 0 M1 = 0;
x1 = 0, 08 M1 = RA· 0, 08 = 837· 0, 08 = 66, 96 Н· м;
На участке х2: M2=RA· x2 – RB (x2 – 0, 08);
x2 = 0, 08 M2 = 66, 96 Н· м;
x2 = 0, 08 + 0, 09 M2 = RA· 0, 17 – RB (0, 17 – 0, 08) = 837· 0, 17 – 1581· 0, 09 = 0 Н· м;
6. 3 Расчет вала на статическую прочность при действии пиковой нагрузки
Выбираем значение коэффициента S запаса прочности
[S] = 2, 0.
6. 3. 1 Коэффициент перегрузки принимается
КП = 2, 2 – коэффициент пиковой нагрузки.
6. 3. 2 Определение нормальных σ и касательных τ напряжений в опасном сечении вала при действии пиковой нагрузки
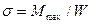 ; (6. 1)
; (6. 1)
 , (6. 2)
, (6. 2)
где  - изгибающий момент, Н· мм;
- изгибающий момент, Н· мм;
 - крутящий момент, Н· мм;
- крутящий момент, Н· мм;
W и WK – моменты сопротивления сечения вала при расчете на изгиб и кручение, мм3;
 ;
;
 ;
;
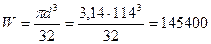 ;
;
 ;
;
 МПа;
МПа;
 МПа.
МПа.
6. 3. 3 Определяем частные коэффициенты запаса прочности по нормальным и касательным напряжениям.
|
|
|
 ; (6. 3)
; (6. 3)
 , (6. 4)
, (6. 4)
где 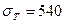 МПа,
МПа,  МПа – пределы текучести [4, с. 165].
МПа – пределы текучести [4, с. 165].
 ;
;
 .
.
6. 3. 4 Определяем общий коэффициент запаса прочности по пределу текучести.
 . (6. 5)
. (6. 5)
 .
.
Условие прочности выполнено, поэтому вал пригоден.
6. 4 Расчет вала на усталостную прочность
Вычисляем коэффициент запаса прочности S [4, с. 169]
 , (6. 6)
, (6. 6)
где Sσ и Sτ - коэффициенты запаса по нормальным и касательным напряжениям, определяемые по зависимостям
 , (6. 7)
, (6. 7)
 , (6. 8)
, (6. 8)
где σ a и τ a — амплитуды напряжений цикла; σ m и τ m — средние напряжения цикла; ψ σ = 0, 1 и ψ τ =0, 05 — коэффициенты чувствительности к асимметрии цикла напряжений для рассматриваемого сечения.
В расчетах валов принимают, что нормальные напряжения изменяются по симметричному циклу: σ a = σ и и σ m = 0, а касательные напряжения — по отнулевому циклу: τ a = τ k /2 и τ m = τ k /2.
Тогда
 , (6. 9)
, (6. 9)
 , (6. 10)
, (6. 10)
 Н· мм;
Н· мм;
 Н· мм;
Н· мм;
 МПа;
МПа;
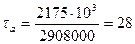 МПа;
МПа;
Пределы выносливости σ -1 и τ -1 [4, с. 165]
 МПа;
МПа;
 МПа.
МПа.
Кσ = 1, 9 и Кτ = 1, 4 – эффективные коэффициенты концентрации напряжений при изгибе и кручении.
Кd = 0, 68 и КF = 0, 8 – масштабный фактор и фактор шероховатость поверхности.
|
|
|
 ;
;
 ;
;
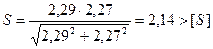 =2, 0.
=2, 0.
Условие прочности выполнено, поэтому вал пригоден.
7 РАСЧЕТ ВАЛА ПРОМЕЖУТОЧНОЙ ОПОРЫ
7. 1 Расчет реакций в опорах

Рисунок 7. 1 - Расчетная схема нагружения вала
Для определения реакции в опоре А составляем уравнение суммы сил относительно точки A и приравниваем его к нулю, т. к. конструкция находится в уравновешенном состоянии.
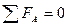 ;
;
 ;
;
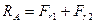 ;
;
Подставляем численные значения известных элементов данного уравнения
 Н.
Н.
Подставляем численные значения известных элементов данного уравнения
7. 2 Расчет эпюры изгибающих моментов вала
На участке х1: M1=Fr1· x1;
x1 = 0 M1 = 0;
x1 = 0, 17 M1 = Fr1· 0, 17 = 744· 0, 17 = 126 Н· м;
На участке х2: M2= Fr1· x2 – RA (x2 – 0, 17);
x2 = 0, 17 M2 = 126 Н· м;
x2 = 0, 17 + 0, 17 M2 = Fr1· 0, 17 – RA · 0, 17 = 744· 0, 34 – 1488· 0, 17 = 0 Н· м;
6. 3 Расчет вала на статическую прочность при действии пиковой нагрузки
Выбираем значение коэффициента S запаса прочности
[S] = 2, 0.
6. 3. 1 Коэффициент перегрузки принимается
КП = 2, 2 – коэффициент пиковой нагрузки.
6. 3. 2 Определение нормальных σ и касательных τ напряжений в опасном сечении вала при действии пиковой нагрузки
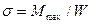 ; (6. 1)
; (6. 1)
 , (6. 2)
, (6. 2)
где  - изгибающий момент, Н· мм;
- изгибающий момент, Н· мм;
 - крутящий момент, Н· мм;
- крутящий момент, Н· мм;
W и WK – моменты сопротивления сечения вала при расчете на изгиб и кручение, мм3;
 ;
;
 ;
;
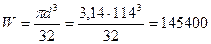 ;
;
 ;
;
 МПа;
МПа;
 МПа.
МПа.
6. 3. 3 Определяем частные коэффициенты запаса прочности по нормальным и касательным напряжениям.
 ; (6. 3)
; (6. 3)
 , (6. 4)
, (6. 4)
где 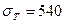 МПа,
МПа,  МПа – пределы текучести [4, с. 165].
МПа – пределы текучести [4, с. 165].
 ;
;
 .
.
6. 3. 4 Определяем общий коэффициент запаса прочности по пределу текучести.
 . (6. 5)
. (6. 5)
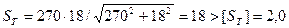 .
.
Условие прочности выполнено, поэтому вал пригоден.
|
|
|


