 |
Цепь, содержащая емкостный элемент с емкостью с
|
|
|
|
В радиоэлектронных устройствах емкость является элементом колебательных контуров, фильтров, элементом связи между контурами и т. п. В силовых установках конденсаторы используют для улучшения коэффициента мощности, как элемент колебательного контура высокочастотных установок для закалки и плавки металлов. В любой электрической установке емкости образуются между проводами, проводами и землей и другими элементами токоведущих конструкций.
При большой протяженности проводов емкость может оказаться значительной, и при расчете цепей даже низкой, например промышленной, частоты ее необходимо учитывать. В высокочастотных цепях даже небольшие емкости оказывают существенное влияние на режим работы цепи и их необходимо учитывать.
Ток в цепи с емкостью (рис. 2.8, а) представляет собой движение зарядов к ее обкладкам:
i = dq/dt. (2.10)
Выразив в (2.10) заряд q через емкость С и напряжение на емкости иС, из выражения
С = q/uС
получим
i = CduС /dt.
Напряжение на емкости изменяется синусоидально:
и = иС = Um sin ωt. (2.11)
Тогда ток в цепи
Взяв производную, получим мгновенное значение тока в цепи с емкостью:
i = ωCUm cos ωt = Im sin (ωt + π/2). (2.12)
Сравнивая выражения (2.11) и (2.12), можно сделать вывод, что ток в емкости опережает напряжение на емкости по фазе на 90°.
Векторная диаграмма цепи с емкостью приведена на рис. 2.8, б, а график мгновенных значений тока и напряжения — на рис. 2.8, в.
Рис. 2.8. Электрическая цепь, содержащая емкостный элемент с емкостью С (а), ее векторная диаграмма (б) и графики мгновенных значений u, i, p (в)
Напряжение и ток в цепи с емкостью, как следует из выражения (2.12), связаны соотношением
Im = ωCUm,
откуда
(2.13)
Разделив левую и правую части (2.13) на 
, получим закон Ома для цепи с емкостью:
|
|
|
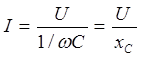(2.14)
где хС = 1/ωC — емкостное сопротивление, Ом.
Таким образом, напряжение на емкости в цепи переменного тока может быть выражено через произведение тока на емкостное сопротивление:
U = UC = IхC.
Мгновенное значение мощности р в цепи с емкостью равно произведению мгновенных значений напряжения и тока:
Из полученного выражения вытекает, что мгновенная мощность изменяется по закону синуса с частотой, в 2 раза большей частоты тока, и ее амплитудное значение
Рт = UI.
Среднее значение мощности за период (активная мощность), как видно из графика рис. 2.8, в, равно нулю:
Для пояснения энергетических процессов в цепях с емкостью воспользуемся графиками, изображенными на рис. 2.8, в. В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на конденсаторе возрастает, происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. Накопленная энергия равна заштрихованной площади, ограниченной кривой р(t) (отмечена знаком «+»), и составляет
В следующую четверть периода, в интервале времени между точками 2 и 3, ток изменяет направление, а напряжение на конденсаторе убывает. Происходит разряд конденсатора: энергия электрического поля возвращается в сеть. Энергия, возвращенная в сеть, равна площади, ограниченной кривой р (t) (отмечена знаком «-»).
Из графиков рис. 2.8, в видно, что площади, определяющие запасенную и отданную энергии, равны. Следовательно, энергия, накопленная в электрическом поле емкости в первую четверть периода, полностью возвращается в сеть во вторую четверть периода.
В следующую четверть периода, в интервале времени между точками 3 и 4, изменяется полярность напряжения на обкладках конденсатора. Происходит заряд конденсатора: электрическая энергия из сети поступает к конденсатору и накапливается в нем в виде энергии электрического поля. В последнюю четверть периода, в интервале между точками 4 и 5, происходит разряд конденсатора: энергия электрического поля возвращается в сеть.
|
|
|
Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, происходит непрерывный периодический процесс обмена энергией между сетью и конденсатором.
|
|
|
