 |
Степенная зависимость в биологии
|
|
|
|
Говорят, что в Лондоне между любым человеком и крысой расстояние меньше двух метров. Хозяева ночи, днем крысы дремлют в подвалах или сточных трубах. Если вы читаете эту книгу перед сном, то, может быть, они как раз проснулись и устроили возню в кухне (не волнуйтесь, я имею в виду кухню соседнего дома). Возможно, какие-то особи уже тихо разлагаются где-нибудь на помойке, так как дольше трех лет крысы обычно не живут. Крысы, некогда страшные вестники бубонной чумы, до сих пор символизируют мерзость запустения. Тем не менее мы перед ними в неоплатном долгу. Лабораторные крысы, чистые и опрятные родичи обитателей помоек, помогли нам переписать учебники по медицине, послужив объектами для изучения человеческих болезней и (фигурально выражаясь) подопытными кроликами при тестировании многих новых способов лечения. Крысы прекрасно подходят на роль подопытных животных потому, что во многих отношениях похожи на нас. Они тоже млекопитающие, у них есть те же органы, что и у нас, они расположены сходным образом и имеют схожие основные функции. Кроме того, крысы в некотором отношении имеют человеческие «чувства и чувствительность», например, проявляют живое любопытство к происходящему вокруг. В старости крысы страдают от «человеческих» болезней, таких как рак, атеросклероз, диабет, катаракта и другие, но исследователям не нужно ждать семьдесят лет, чтобы проверить действенность какого-нибудь лекарства, а достаточно подождать пару лет. Как и мы, крысы от скуки начинают переедать, а потом страдают ожирением. Всякий, кто держал дома крысу, знает, как важно оградить питомца от перекорма и безделья. Лакомство лучше спрятать, пускай ищет сам.
|
|
|
Мы так близки к крысам (во всех смыслах), что вы, возможно, удивитесь, узнав, насколько быстрее работают все их органы. Сердце, легкие, печень, почки, кишечник работают у крыс в среднем в семь раз интенсивнее, чем у нас (но к скелетным мышцам это не относится). Сейчас я объясню, что имею в виду. Представьте, что современный Шейлок получил-таки если не фунт, то грамм плоти крысы, а также грамм человеческой плоти. Скажем, это были кусочки печени. Оба кусочка содержат примерно одинаковое число клеток, а клетки печени у крыс и людей имеют одинаковый размер. Если мы сможем некоторое время поддерживать ткань в живом состоянии, измеряя при этом ее активность, мы увидим, что грамм печени крысы за минуту потребляет в семь раз больше кислорода и питательных веществ, чем такой же кусочек человеческой печени, хотя под микроскопом они выглядят совершенно одинаково. Хочу подчеркнуть, что это чисто эмпирический факт. Почему это так, мы обсудим в этой главе.
Причины столь существенной разницы в уровне метаболизма не вполне ясны, но последствия очень важны. Поскольку клетки крысы и клетки человека имеют примерно одинаковый размер, отдельная клетка крысы должна работать в семь раз интенсивнее (вспомним гипотетического червя Холдейна, страдающего от геометрических ограничений). Это относится ко всем биологическим аспектам существования организма: каждая клетка должна в семь раз быстрее копировать гены, синтезировать в семь раз больше белков, выкачивать из клеток в семь раз больше солей, очищать организм от семикратного количества токсинов и т. д. Чтобы поддерживать такую высокую скорость обмена веществ, крысы должны есть в семь раз больше пищи, чем люди, в пересчете на размер. А мы еще говорим про волчий аппетит! Даже с крысиным аппетитом мы заказывали бы не обычный стейк, а полуторакилограммовый. Эти базовые математические выкладки не имеют отношения к генам (по крайней мере, они не имеют к ним непосредственного отношения), но отчасти объясняют, почему крысы живут три года, а нам отведены «дней лет наших — семьдесят лет[47]».
|
|
|
Крысы и люди — точки на удивительной кривой, соединяющей землероек, одних из самых мелких млекопитающих, с самыми большими — слонами и синими китами (см. рис. 12).

Рис. 12. График зависимости уровня метаболизма в состоянии покоя от массы тела у млекопитающих разного размера, от мыши до слона. Наклон прямой на графике с логарифмическим масштабом на обеих осях составляет ¾ (0,75), то есть при подъеме на три деления по вертикальной оси она проходит четыре деления по горизонтальной оси. Этот наклон и соответствует показателю степени ¾. Уровень метаболизма изменяется пропорционально массе в степени ¾ (m¾)
Никто не спорит, что большие животные потребляют больше пищи и кислорода, чем маленькие. Однако при удвоении массы тела потребление кислорода, против ожидания, не возрастает вдвое. С удвоением массы удваивается и общее число клеток. Если каждой клетке нужно одинаковое количество энергии для жизни, то удвоение массы должно удваивать и количество необходимой пищи и кислорода. Это предполагает точную эквивалентность: при увеличении массы тела уровень метаболизма должен повышаться прямо пропорционально. Тем не менее это не так. С увеличением размеров тела животных клеткам их тела нужно меньше питательных веществ для жизни. Большие животные имеют более низкий уровень метаболизма, чем можно было бы ожидать. Приращение массы отзывается чуть меньшим приращением уровня метаболизма. Мы уже рассмотрели семикратную разницу между крысой и человеком. Чем больше животное, тем меньше пищи на грамм собственного веса ему нужно. Возьмем, скажем, слона и мышь: если мы выясним, сколько пищи нужно для поддержания жизнедеятельности каждой клетки (или на грамм массы), то окажется, что слону ежеминутно нужно в 20 раз меньше пищи и кислорода, чем мыши. Если посмотреть с другой стороны, гора мышей размером со слона будет потреблять в 20 раз больше пищи и кислорода в минуту, чем сам слон. Ясно, что быть слоном экономически выгодно, но объясняет ли эта выгода эволюционную тенденцию к увеличению размера и усложнению?
|
|
|
Уровень метаболизма определяется через потребление кислорода и питательных веществ. Если уровень метаболизма падает, каждая клетка потребляет меньше пищи и кислорода. И если все клетки тела потребляют меньше кислорода, то частота дыхания, частота сердцебиения и т. д. могут позволить себе замедлиться. Вот почему сердце слона бьется так медленно по сравнению с трепетанием мышиного сердца: отдельным клеткам слона нужно меньше пищи и кислорода, поэтому сердцу слона не нужно биться так быстро, чтобы обеспечить всем этим клетки (что, правда, предполагает одинаковое соотношение размеров сердца и общего размера тела у мыши и слона). Еще одно неожиданное следствие — замедление старения. Мыши живут 2–3 года, а слоны около 60 лет, хотя их сердца делают за всю жизнь сходное число ударов, а клетки тела потребляют примерно одинаковое количество кислорода и пищи (слон за 60 лет, а мышь за три года). Такое впечатление, что клетки могут сжигать строго определенное количество энергии, но слон «выжигает» свою долю медленнее, чем мышь. Очевидно, это связано с тем, что слон больше. Эта закономерность глубинным образом сказывается на экологии и эволюции. Размер животных влияет на плотность популяций, расстояние, которое они способны покрыть за день, число потомков, репродуктивный возраст, скорость смены поколений в популяции и темпы эволюционного процесса, например видообразования. Подобные показатели можно предсказать с поразительной точностью, зная всего лишь уровень метаболизма отдельных животных.
Более века биологи, физики и математики ломали голову над тем, почему уровень метаболизма варьирует в зависимости от размера. Первым, кто подошел к проблеме систематически, был немецкий физиолог Макс Рубнер. В 1883 г. он составил графики уровня метаболизма семи собак, масса которых варьировала от 3,2 до 31,2 кг. Нанесенные на график данные образуют плавную кривую. Если использовать логарифмическую шкалу по обеим осям, то точки хорошо ложатся на прямую линию. График в логарифмическом масштабе удобен по разным причинам, но в основном потому, что на нем четко виден множитель: вместо того, чтобы пошагово добавлять значения на фиксированном расстоянии на оси (10 + 10 + 10 и т. д.), график в логарифмическом масштабе умножает их (10 х 10 х 10 и т. д,). Это позволяет увидеть, сколько умножений одного параметра соответствуют умножениям другого. Давайте рассмотрим простой куб. Если мы нанесем логарифм площади поверхности на одну ось и логарифм объема на другую, мы получим график того, как они будут меняться относительно друг друга при увеличении размера куба. На каждое десятикратное увеличение ширины куба мы получаем стократное увеличение его площади поверхности и тысячекратное увеличение объема. Если мы используем график с логарифмическим масштабом на обеих осях, тысячекратное увеличение площади поверхности соответствует двум шагам, а увеличение объема — трем. Это определяет угол наклона прямой. В случае куба угол наклона равен ⅔, или 0,67, — каждым двум шагам увеличения площади поверхности соответствуют три шага увеличения объема. Угол наклона соединяющей точки прямой — это показатель степени, которая обычно записывается в виде надстрочного знака после числа, к которому относится; в данном случае показатель степени записывается как ⅔. По определению показатель степени указывает, сколько раз число должно быть умножено на себя (так, 22 = 2 х 2, а 24 = 2 х 2 х 2 х 2). Однако когда мы имеем дело с дробными показателями степени, такими как ⅔, гораздо проще рассматривать ситуацию с точки зрения наклона прямой на графике с логарифмическим масштабом на обеих осях. Если показатель степени равен 1, это означает, что каждый шаг по одной оси соответствует такому же шагу по другой: два параметра прямо пропорциональны. Если показатель степени равен ¼, это означает, что каждый шаг по одной оси соответствует четырем шагам по другой: отношение постоянно, но не прямо пропорционально.
|
|
|
Вернемся к Максу Рубнеру. Нанеся на одну ось логарифм уровня метаболизма, а на другую — логарифм массы, Рубнер открыл, что уровень метаболизма пропорционален массе тела в степени ⅔. Иными словами, с повышением логарифма уровня метаболизма на два шага логарифм массы повышался на три шага. Это, как вы уже догадались, то же самое отношение, что и соотношение площади поверхности и объема куба. Рубнер, изучавший собак, объяснил это соотношение с точки зрения потери тепла. Количество тепла, выделяющегося в процессе обмена веществ, зависит от числа клеток, а скорость теплоотдачи в окружающую среду зависит от площади поверхности (так, количество тепла, излучаемого батареей, зависит от площади ее поверхности). С увеличением размера масса растет быстрее, чем площадь поверхности. Если все клетки будут отдавать тепло с одинаковой скоростью, общий уровень теплопродукции будет расти с ростом массы тела, а вот теплоотдача будет зависеть от площади поверхности. Более крупные животные будут сохранять больше тепла. К примеру, слон просто бы расплавился, если бы его клетки производили тепло с той же скоростью, что клетки мыши. Получается, смысл высокого уровня метаболизма — это сохранение тепла, а большие животные сохраняют тепло лучше маленьких, и слону не так уж нужен высокий уровень метаболизма: достаточно, чтобы температура тела была постоянной и составляла примерно 37 °C. Итак, по мере того как животные увеличиваются в размерах, уровень их метаболизма замедляется в число раз, равное соотношению площади поверхности к массе тела.
|
|
|
Рубнер, конечно, имел дело только с одним видом животных, хотя разные породы собак сильно отличаются по размеру и внешнему виду. Полвека спустя Макс Клайбер — швейцарский физиолог, позже работавший в США, — составил график зависимости логарифма уровня метаболизма от логарифма массы у разных видов и получил свою знаменитую кривую от мышей до слонов. К всеобщему, а также его собственному удивлению, показатель степени составил не ⅔, а ¾ (0,75; или, если совсем точно, 0,73; рис. 12). Иными словами, с повышением логарифма уровня метаболизма на три шага логарифм массы повышался на четыре. К подобному выводу пришли и другие исследователи, в частности американец Сэмьюэл Броди. Еще более неожиданным было то, что показатель степени 0,75 характеризовал не только млекопитающих. На этой кривой прекрасно разместились птицы, рептилии, рыбы, насекомые, деревья и даже одноклеточные организмы: зависимость уровня метаболизма от массы тела в степени ¾ (m¾) действительна для всех организмов в пределах 21 порядка величины! Пропорционально показателю степени, основанному на кратных одной четверти величинах (например, ¼ или ¾), изменяются и многие другие признаки, например частота пульса, диаметр аорты, диаметр стволов деревьев и продолжительность жизни. «Метаболический закон трех четвертей», или «закон Клайбера», вошел практически во все учебники биологии, хотя некоторые исследователи (в частности, Альфред Хойзнер из Калифорнийского университета в Дэвисе) оспаривают его универсальность. Закон Клайбера часто называют одним из немногих универсальных биологических законов[48].
Почему уровень метаболизма изменяется пропорционально массе в степени ¼) оставалось загадкой почти полвека; на самом деле, ответ забрезжил только в последнее время. Один аспект загадки был очевиден. Показатель степени ⅔, связывающий уровень метаболизма с соотношением площади поверхности к объему, поддавался какому-то объяснению в случае теплокровных животных (млекопитающих и птиц), но было совершенно непонятно, почему он приложим к холоднокровным животным, например рептилиям и насекомым. Они не производят тепло внутри тела (или, по крайней мере, производят очень мало), и баланс теплопродукции и теплоотдачи вряд ли мог иметь решающее значение. С этой точки зрения хоть три четверти, хоть две трети — один черт. Обосновать закон трех четвертей пытались многие, но ни одно объяснение не выглядело убедительным.
Затем физик Джеффри Вест из Лос-Аламосской национальной лаборатории (США) объединил усилия с экологами Джеймсом Брауном и Брайеном Энквистом из Университета штата Нью-Мексико в Альбукерке (в рамках Института Санта-Фе, содействующего междисциплинарным исследованиям сложных систем). Они предложили радикально новое объяснение, основанное на фрактальной геометрии разветвленных распределительных сетей, таких как система кровообращения млекопитающих, трахейная система насекомых и сосудистая система растений. Их насыщенная математикой модель была опубликована в журнале Science в 1997 г., и если математическая составляющая была доступна лишь избранным, выводы этого исследования вскоре овладели многими умами.
Фрактальное древо жизни
Фракталы (от лат. fractus — сломанный) — это геометрические формы, которые выглядят одинаково при любом масштабировании. Если разбить фрактал на составляющие части, они будут более или менее одинаковы, потому что, как сформулировал основоположник фрактальной геометрии Бенуа Мандельброт, «эти фигуры состоят из частей, некоторым образом похожих на целое». Фракталы могут образовываться случайно под действием природных сил, таких как ветер, дождь, замерзание, эрозия и сила тяжести. Тогда получаются естественные фракталы — горы, реки, береговая линия, облака. Мандельброт называл фракталы «геометрией природы». В эпохальной статье, опубликованной в журнале Science в 1967 г., он использовал этот подход для решения вопроса, вынесенного в заглавие «Какова протяженность побережья Великобритании?». Фракталы можно генерировать математически; для этого часто используют повторяющуюся геометрическую формулу, задающую угол и плотность ветвления («фрактальная размерность»).
Природные и математические фракталы имеют общее свойство — масштабную инвариантность. Это значит, что они выглядят одинаково при любом увеличении. Например, очертания скалы часто похожи на очертания утеса или даже горы. Именно поэтому геологи, фотографируя объект, кладут рядом с ним молоток, чтобы потом по фотографии можно было сразу получить представление о масштабе объекта. Точно так же и растекающиеся водные потоки любой континентальной системы выглядят очень похоже: это может быть бассейн реки Амазонки, наблюдаемый из космоса, маленькие ручейки, видимые с вершины холма, или даже размытая водой грядка при взгляде из окна загородного дома. В случае математических «итеративных» фракталов, повторяющееся геометрическое правило позволяет получить бесконечное число подобных форм. Даже самые сложные и красивые фракталы, украшающие футболки и постеры, получаются за счет многократных повторений одних и тех же геометрических правил (зачастую весьма хитроумных) и нанесения получившихся точек на поверхность. Для большинства из нас футболка с фрактальным принтом — единственная возможность приобщиться к красоте глубокой математики.
Большинство природных фракталов на самом деле не настоящие фракталы, потому что их масштабная инвариантность не бесконечна. И все же узор ветвления каждой ветки примерно повторяет характер ветвления дерева как целого, а ветвление кровеносных сосудов в любой ткани или органе — их ветвление во всем организме. Видя только один узор, оценить масштаб зачастую непросто. Сердечно-сосудистая система слона напоминает аналогичную систему мыши, хотя она увеличена почти на шесть порядков (в миллион раз). Если сети выглядят похожими при столь существенных изменениях масштаба, то самым естественным языком для их описания является фрактальная геометрия. Пусть ветвящиеся системы природы и не настоящие фракталы, но они достаточно приближены к ним, чтобы их было можно моделировать с использованием соответствующих математических принципов.
Вест, Браун и Энквист задумались о том, не объясняет ли фрактальная геометрия природных «распределительных сетей» почти универсальную зависимость уровня метаболизма от размера тела. Это было бы логично, ведь уровень метаболизма соответствует потреблению пищи и кислорода, а они поступают в отдельные клетки животного не через поверхность тела, а как раз-таки через ветвящуюся «распределительную сеть», в данном случае кровеносные сосуды. Если уровень метаболизма ограничен доставкой этих питательных веществ, резонно предположить, что он должен по большому счету зависеть от свойств распределительной сети. В статье, опубликованной в журнале Science в 1997 г., Вест, Браун и Энквист сделали три основных допущения. Во-первых, сеть обслуживает весь организм (доставляет питательные вещества ко всем его клеткам) и поэтому должна заполнять весь объем организма. Во-вторых, капилляр — мельчайшее ответвление кровеносной системы — имеет инвариантный размер, то есть размер капилляров одинаков у всех животных независимо от размеров их тела. И в-третьих, они предположили, что питательные вещества должны распределяться по сети с минимальными затратами энергии и времени, и в процессе эволюции естественный отбор соответствующим образом оптимизирует распределительную сеть.
Ученым нужно было принять во внимание и некоторые другие факторы, связанные с эластичностью сосудов, но мы не будем углубляться в дебри. Итог таков: для поддержания самоподобной фрактальной сети (то есть такой, которая выглядит одинаково в любом масштабе) при пропорциональном увеличении размеров тела на несколько порядков общее число ветвей сети увеличивается медленнее, чем объем тела. Наблюдения показывают, что это действительно так. Например, кит в десять миллионов (107) раз тяжелее мыши, а ответвлений от аорты к капиллярам у него только на 70 % больше. Согласно идеализированным расчетам фрактальной геометрии, в крупном животном распределительная сеть должна занимать относительно меньше места; каждый капилляр обслуживает большее число «конечных пользователей» (клеток). Это означает, что количество пищи и кислорода, распределяемое «на всех», уменьшается, а клеткам, получающим меньше пищи, придется понизить уровень метаболизма. Понизить насколько? Фрактальная модель предсказывает, что уровень метаболизма должен соответствовать массе тела в степени ¾. Представьте себе это в виде наклона прямой на графике с логарифмическим масштабом на обеих осях: на каждые три шага по оси с логарифмом уровня метаболизма приходятся четыре шага на оси с логарифмом массы. Иными словами, фрактальная модель Веста, Брауна и Энквиста предсказывает, что уровень метаболизма должен изменяться пропорционально массе в степени ¾. Таким образом, она объясняет метаболический закон ¾ (закон Клайбера). Если это объяснение верно, то все живые организмы подчиняются правилам фрактальной геометрии. Они определяют размер тела, плотность популяций, продолжительность жизни, темпы эволюции — вообще всё.
Но и это еще не предел. Фрактальная модель идет дальше, делая радикальное предсказание. Мы уже говорили, что закон Клайбера, как кажется, применим не только к большим организмам, у которых есть явная ветвящаяся распределительная сеть (млекопитающие, насекомые, деревья), но и к простым существам, у которых, на первый взгляд, такой сети нет (отдельные клетки). Вест, Браун и Энквист предположили, что простые организмы тоже имеют какую-то фрактальную распределительную сеть. Это действительно радикальное предположение, так как оно предполагает существование уровня биологической организации, который до сих пор не был нами обнаружен, и даже сторонники фрактальной теории осторожно говорят о некоей «виртуальной» сети. Тем не менее многие биологи не склонны с ходу отметать это предположение, так как в последнее время стало ясно, что цитоплазма — это нечто куда более сложное, чем аморфный гель, который описывается в учебниках. Характер ее организации пока что ускользает от понимания, но ясно, что потоки цитоплазмы «струятся» по клетке, а многие биохимические реакции гораздо жестче приурочены к определенным пространственным точкам, чем считалось ранее. Большинство клеток имеют сложную внутреннюю архитектуру, в том числе разветвленные сети волокон цитоскелета и сети митохондрий. Но действительно ли эти внутриклеточные сети являются фрактальными и подчиняются законам фрактальной геометрии? Они, бесспорно, ветвятся (рис. 13), но на древовидные сети циркуляторных систем это не слишком похоже. Фрактальная геометрия описывает самоподобные системы, а во внутриклеточных системах самоподобия не просматривается.
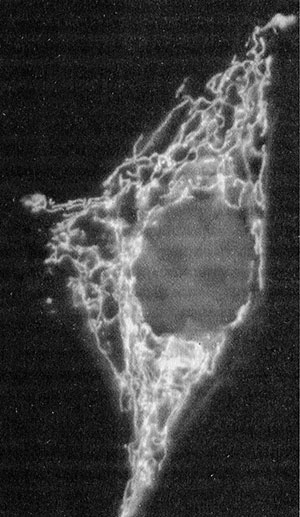
Рис. 13. Сеть митохондрий в клетке культуры ткани млекопитающего, окрашенная красителем MitoTracker. Митохондрии нередко перемещаются по клетке и могут образовывать сетчатые структуры, такие как на этом рисунке. Однако на фрактальное дерево эти сети не похожи
Чтобы решить эти с виду нерешаемые проблемы, Вест, Браун и Энквист модифицировали свою модель. Исключив из нее требование наличия явных ветвящихся сетей, они взяли за основу геометрию иерархических сетей (сетей, которые включены в другие сети, как матрешки). Другие физики (назову Джаянта Банавара из Университета Пенсильвании и его коллег) попробовали упростить сетевую модель, вообще исключив из нее фрактальную геометрию, однако их модель тоже предполагает наличие ветвящейся распределительной сети. С конца 1990-х гг. на страницах престижных научных журналов каждые несколько месяцев появляется новая порция мудреных математических выкладок, часто перемежаемых уничижающими отповедями, такими как, например, «это не может быть справедливо, так как нарушает однородность размерностей…». Подобные споры нередко приводят к расколу между биологами, которые слишком часто сталкиваются с исключениями из якобы универсальных законов («в природе все сложнее, чем на самом деле»), и физиками, такими как Вест, которые пытаются найти общую теорию всего. Вест не стесняется в выражениях: «Если бы Галилей был биологом, он исписал бы тысячи страниц, тщательно документируя, что предметы разной формы падают с Пизанской башни с немного разной скоростью. Отвлекаясь на эти мелочи, он упустил бы главное: если не принимать в расчет сопротивление воздуха, все предметы падают с одинаковой скоростью независимо от их массы».
|
|
|


