 |
Схематические и условные изображения кинематических пар
|
|
|
|
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Методические указания
К выполнению домашнего задания по дисциплине «Техническая механика» на тему
«Кинетостатический расчет плоского рычажного механизма»
Методические указания предназначены для студентов направления 270800 Строительство всех форм обучения
Волгодонск 2012
УДК 621.833: 539.4 (076.5)
Рецензент: канд. техн. наук, доц. А.А. Мецлер
Составители – Синельщиков В. В., Пирожков Р. В., Пинчук Э. В.
Техническая механика: методические указания к выполнению домашнего задания по дисциплине «Техническая механика». /Волгодонский инженерно-технический институт (филиал) НИЯУ МИФИ. - Волгодонск: ВИТИ НИЯУ МИФИ, 2012.- с. 37.
Методические указания содержат необходимые данные для проведения кинетостатического анализа плоских рычажных механизмов, варианты задач и пример расчета, а также вопросы для самоконтроля студентов.
Методические указания предназначены для организации самостоятельной работы студентов всех форм обучения квалификации «бакалавр» по направлению подготовки 270800 «Строительство» при выполнении домашнего задания на тему «Кинетостатический расчет плоского рычажного механизма» по дисциплине «Техническая механика».
УДК 621.833: 539.4 (076.5)
© ВИТИ НИЯУ МИФИ, 2012
Содержание
1. Структурный анализ плоского рычажного механизма ………. 4
|
|
|
2. Кинематический анализ плоского рычажного механизма ……15
3. Кинетостатический анализ плоского рычажного механизма …..24
4. Выбор варианта домашнего задания……………………………..33
5. Контрольные вопросы …………………………………………….37
Структурный анализ плоского рычажного
Механизма
Звенья, кинематические пары и их классы
Структурный анализ механизмов проводится с целью определения числа степеней свободы и класса механизма. Класс механизма определяется по классификации Ассура-Артоболевского.Для структурного анализа используют структурно-кинематическую схему механизма – изображение механизма с помощью условных обозначений, выполненное в масштабе.
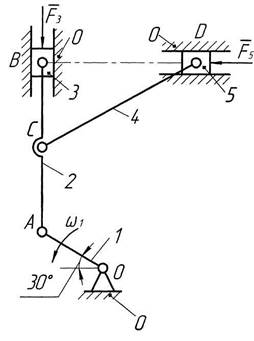
На рис. 1.1 изображена кинематическая схема плоского рычажного механизма. В ее состав входят звенья (0, 1, 2, 3, 4, 5), образующие кинематические пары (1-0, 1-2, 2-3, 3-0, 2-4, 4-5, 5-0). Название звеньев: 1 – кривошип, 2 – шатун, 3 – ползун (поршень), 4 – шатун, 5 – ползун (поршень), 0 – стойка.
| 
| 
|
| ||
| а) | б) |
Рис. 1.1. Кинематическая схема механизма
Рассмотрим некоторые определения и сведения, касающиеся звеньев, кинематических пар и их классификации.
Одно или несколько жестко соединенных тел, входящих в состав механизма, называется звеном. Жестко соединенные тела, образующие звено, называют деталями.
Звено, принимаемое за неподвижное, называют стойкой. Звено, движение которому сообщается за счет приложения внешних сил или моментов сил, называют ведущим. Звенья механизма, положения и перемещения которых однозначно зависят от положений и перемещений ведущего звена, называют ведомыми.
Кинематической парой называют соединение двух соприкасающихся звеньев, допускающее их относительное движение (кинематические пары 1-0, 1-2, 2-3, 3-0, 2-4, 4-5, 5-0, рис. 1.1).
Элементы кинематических пар – поверхности, линии, точки звена, по которым оно может соприкасаться с другим звеном. Если элементом пары является точка или линия, то эти пары называют высшими. К низшим парам относят такие, у которых элементами являются поверхности.
|
|
|
Одним из отличительных признаков кинематической пары является число связей – количество простейших относительных движений, которых лишаются звенья при соединении в кинематические пары.
Известно, что свободное тело в пространстве может совершать шесть независимых простейших движений, три из которых – вращательные вокруг осей x, y, z и три – поступательные вдоль этих осей. В этом случае тело имеет шесть степеней свободы.
Если два звена, например ползун 5 и направляющая неподвижная стойка 0 (рис. 1.1), соединены так, что допустима их относительная подвижность, то они образуют кинематическую пару, причем ползун теряет пять возможных простейших перемещений. Совершенно очевидно, что существуют случаи, когда одно звено механизма в своем движении относительно другого звена может потерять 5, 4, 3, 2 или 1 простейших движений. В соответствии с этим по И. И. Артоболевскому все кинематические пары разделяют на 5 классов. Номер класса кинематической пары определяется числом условий связи, которые наложены на движение одного звена пары относительно другого. Отсюда следует, что у пары 1-го класса одно звено не может совершать относительно другого одно какое-либо движение из шести возможных, т. е. имеет 5 степеней подвижности. Пара 2-го класса имеет звено, которое не может совершать два любых из шести движений, но обладает четырьмя степенями подвижности и т. д.
Класс кинематической пары определяют следующим образом. Одно из звеньев, входящих в кинематическую пару, представляют неподвижным и связывают с ним систему координат xyz. Ориентируясь по ней, необходимо проследить, какие движения другого звена пары невозможны из шести простейших, которые оно имело бы возможность совершать, не входя в пару. Число этих невозможных движений, равное числу связей, определяет номер класса кинематической пары. В табл. 1.1 представлены схематические и условные изображения кинематических пар и указаны их классы.
Кинематические цепи
Кинематической цепью называется совокупность звеньев, соединенных в кинематические пары. Кинематические цепи подразделяются на простые, сложные, замкнутые, незамкнутые.
|
|
|
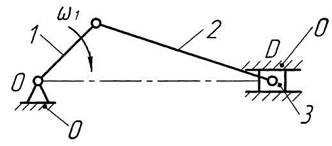
Простой кинематической цепью называется такая, у которой каждое звено входит не более чем в две кинематические пары (рис. 1.2). Кривошипно-шатунный механизм состоит из неподвижного звена – стойки и трех подвижных – 1, 2, 3. Кинематические пары: 1-0, 1-2, 2-3, 3-0. Каждое звено входит не более чем в две кинематические пары.
|
Рис. 1.2. Кинематическая схема кривошипно-шатунного механизма
Таблица 1.1
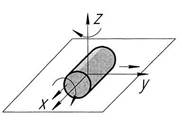
Схематические и условные изображения кинематических пар
| Схематическое изображение кинематических пар | Условное изображение | Число условий связи | Количество свобод относительного движения | Класс кинематической пары |
| Шар на плоскости | 

| |||

| ||||
| Цилиндр на плоскости | 
| |||
|
Продолжение табл. 1.1
| Схематическое изображение кинематических пар | Условное изображение | Число условий связи | Количество свобод относительного движения | Класс кинематической пары |
| Призма на плоскости | 
| |||

| ||||
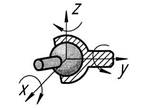
| Сферическая | 
| |||
| ||||
| Сферическая с пальцем | 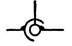
| |||

| ||||
| Цилиндрическая | 
| |||

| ||||
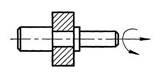
| Вращательная | 

| |||
| ||||
| Поступательная | 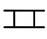
| |||
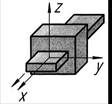
| ||||
| Винтовая | 
| |||

|
Сложной называется такая кинематическая цепь, у которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис. 1.1). Звено 2 входит в следующие кинематические пары 1-2, 2-3, 2-4.
Замкнутой кинематической цепью называется цепь, каждое звено которой входит, по крайней мере, в две кинематические пары (рис. 1.1, 1.2).
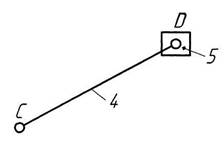
Незамкнутой кинематической цепью называется цепь, у которой есть звенья, входящие только в одну кинематическую пару (рис. 1.3). Звено 5 входит только в одну кинематическую пару 4-5.

|
Рис. 1.3. Кинематическая схема манипулятора
(механизм с незамкнутой кинематической цепью)
С точки зрения структуры механизм – это замкнутая кинематическая цепь, у которой, при заданном движении одного или нескольких звеньев (ведущих) относительно неподвижного звена (стойки), все остальные звенья (ведомые) совершают однозначно определяемые движения.
|
|
|
Для проектируемого механизма необходимо знать, какое количество звеньев, связанных со стойкой, должно быть ведущими для того, чтобы движение механизма было вполне определенным. Для этого вычисляют число степеней свободы W механизма относительно стойки, которое показывает количество ведущих звеньев.
Большинство механизмов, используемых в технике, имеют число степеней свободы, равное единице и, следовательно, должны иметь одно ведущее звено. Все механизмы можно разделить на плоские и пространственные. У плоского механизма точки его звеньев описывают траектории, лежащие в параллельных плоскостях. У пространственного механизма точки его звеньев описывают неплоские траектории, лежащие в пересекающихся плоскостях.
Классы механизмов
Кинематическая схема механизма дает полное представление о структуре механизма и определяет его кинематические свойства. Она выполняется графическим способом с использованием условных обозначений звеньев, кинематических пар и указанием размеров, которые необходимы для кинематического анализа механизма.
На кинематических схемах механизмов звенья изображаются отрезками прямых и нумеруются арабскими цифрами. Кинематические пары обозначаются заглавными буквами латинского алфавита и схематически изображаются так, как показано на рис. 1.4. Элементы высших кинематических пар очерчиваются кривыми, которыми они характеризуются в натуральном виде.

| – шарнирное соединение двух подвижных звеньев (1, 2) (вращательная кинематическая пара A,Vкласса) | |
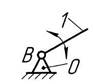 
| – шарнирное соединение подвижного звена 1 со стойкой 0 (вращательная кинематическая пара В,Vкласса) | |
 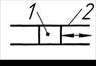

| – соединение двух подвижных звеньев (поступательная кинематическая пара Vкласса) | |
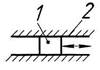 
| – соединение подвижного звена 1 со стойкой 2 (поступательная кинематическая пара Vкласса) | |
 
| – шарнирное соединение двух звеньев, если одно из звеньев не заканчивается в шарнире (вращательная кинематическая пара A,Vкласса) | |
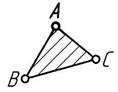
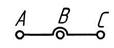
| – звено, входящее в три кинематические пары |
Рис. 1.4. Схематическое изображение кинематических пар
Механизмы подразделяются на классы. В основу классификации положен принцип структурного образования механизмов, сформулированный в 1914 году русскими учеными Л. В, Ассуром и И. И. Артоболевским. Согласно этому принципу схема любого механизма может быть составлена последовательным присоединением к ведущему звену (или к ведущим звеньям) и стойке кинематических цепей с числом степеней свободы, равным нулю, т. е.  . Такие кинематические цепи называют структурными группами или группами Ассура. Группа Ассура – это кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающуюся на более простые цепи с нулевой степенью свободы.
. Такие кинематические цепи называют структурными группами или группами Ассура. Группа Ассура – это кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающуюся на более простые цепи с нулевой степенью свободы.
|
|
|
Согласно структурной формуле Чебышева для плоской кинематической цепи число степеней свободы механизма можно вычислить следующим образом:
 ,
,
где  – число подвижных звеньев;
– число подвижных звеньев; 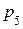 – число пар V класса;
– число пар V класса; 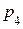 – число пар IV класса.
– число пар IV класса.
Таким образом, для структурной группы (группы Ассура) можно записать:
 .
.
При составлении схемы механизма из кинематических цепей рассматриваются структурные группы, включающие в себя только кинематические пары V класса. Если же исследуемый механизм имеет пары IV класса, они определенным образом заменяются двумя кинематическими парами V класса.
Запишем  , откуда
, откуда  , т. е. число кинематических пар V класса, входящих в структурную группу, должно равняться
, т. е. число кинематических пар V класса, входящих в структурную группу, должно равняться  числа входящих в нее подвижных звеньев. Так как число кинематических пар может быть только целым, то число звеньев группы должно быть только четным. Следовательно, могут иметь место только следующие сочетания чисел подвижных звеньев
числа входящих в нее подвижных звеньев. Так как число кинематических пар может быть только целым, то число звеньев группы должно быть только четным. Следовательно, могут иметь место только следующие сочетания чисел подвижных звеньев  и кинематических пар V класса
и кинематических пар V класса 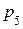 , входящих в структурную группу Ассура (табл. 1.2).
, входящих в структурную группу Ассура (табл. 1.2).
Таблица 1.2
|
|
|


