Кинетостатика плоского рычажного механизма

Методика определения сил в кинематических парах

Кинетостатический или силовой расчет механизмов основан на использовании принципа Даламбера: если в каждый момент времени к активным силам, действующим на звенья работающего механизма, и силам реакций связей добавить силы инерции звеньев, то к полученной системе сил, находящейся в равновесии, можно применить уравнения равновесия статики. Используя эти уравнения равновесия можно рассчитывать реакции, возникающие, например, в шарнирах кинематических пар.

Последовательность силового расчета механизма следующая:

а) механизм разбивают на группы Ассура и рассматривают равновесие каждой группы, так как добавление сил и моментов сил инерции делает статически определимой систему действующих активных сил и возникающих реакций в этой группе;

б) составляют уравнения равновесия плоской системы сил для всей группы Ассура или для отдельных ее звеньев в виде

, , (3.1)

где – векторы сил, действующих на группу; 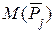– моменты сил относительно некоторой выбранной точки;

в) решают первое уравнение (3.1) графически – путем построения плана сил, а второе – аналитически.

Запись 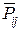принимают как силу реакции, действующую со стороны звена “ i ” на звено “ j ”, а – принимают как реакцию, действующую со стороны звена “ j ”на звено“ i ”. Очевидно, что по третьему закону Ньютона.

 

Кинетостатический расчет механизма без учета сил трения

Расчет начинают с группы, наиболее удаленной от начального звена. Используется графоаналитический метод силового расчета, так как он может быть применим для статически определимых плоских систем сил, нагружающих группы Ассура.

Исходные данные для расчета: длины звеньев 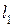, , 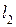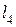(м), массы звеньев , , , (кг), активные силы, действующие на ползуны , (Н).

Механизм (рис. 1.1) разбивают на группы Ассура, которые представляют собой диады 5-4, 2-3 и начальный механизм 0-1 первого класса. Изображают диаду 5-4 в масштабе 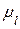(рис. 3.1) и обозначают активные, реактивные силы, силы инерции и моменты сил инерции, действующих на звенья диады.

Рис. 3.1. Плоская система сил, действующих на диаду 5-4

На рис. 3.1: – активная сила; , – силы инерции; – реакция со стороны звена 2 на звено 4; , – нормальная и касательная (тангенциальная) составляющие реакции ; – момент сил инерции, действующих на звено 4; 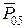– реакция со стороны стойки.

Используя планы скоростей и ускорений, определяют силы инерции и моменты сил инерции. Вектор силы инерции для звена 5, совершающего поступательное движение, направлен противоположно вектору ускорения точки D звена 5. Запишем

.

Величина силы 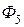, (Н):

,

где – масса звена 5, кг; – величина ускорения точки D, вычисляемая с использованием плана ускорений, .

Так как звено 4 совершает плоское движение, то инерционные нагрузки, действующие на него, приводятся к силе инерции и моменту сил инерции , величины которых определяются по следующим формулам

(Н);

(Н×м),

где – масса звена 4, кг; 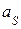– величина ускорения точки S, расположенной посередине звена 4, ; – угловое ускорение звена 4, принимаемое из расчетов плана ускорений, ; 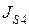– центральный момент инерции звена 4, :

.

Ускорение точки S определяют следующим образом: на плане ускорений соединяем точки “ с ”, “ d ”и делим этот отрезок на две равные части, так как точки S делит звено CD пополам. Отрезок является изображением вектора в масштабе.

.

Вектор направляем в противоположную сторону вектора . Момент сил инерции направлен против ускорения .

Силами тяжести звеньев пренебрегают, считая их малыми по сравнению с другими силами.

Для выделенной группы применяют методы статики, которые позволяют определить неизвестные реакции.

Пользуются уравнениями равновесия в виде суммы моментов сил относительно точки D, что позволяет определить составляющую , Н:

; ,

где h – плечо силы . Натуральную величину плеча h, м, определяют с использованием кинематической схемы механизма, изображенной в масштабе :

,

где – масштабный коэффициент, используемый для построения кинематической схемы механизма, :

.

Если после вычисления , то действительное направление вектора противоположно указанному на чертеже. В этом случае изменяют направление вектора на противоположное и принимают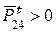

Для рассматриваемой диады записывают векторное уравнение сил

; .

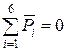В этом уравнении реакци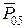и и необходимо определить. Они неизвестны по величине, но известны по направлению. Их значения можно определить, решая уравнение графически – построением плана сил.

Построение плана сил выполняется следующим образом. Из произвольной точки “ a ” откладываютвыбранный отрезок, который в масштабе изображает вектор силы 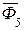. Отрезок проводят параллельно направлению вектора силы . Вычисляют масштабный коэффициент , :

,

где 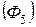– отрезок из точки “ a ” в мм.

Затем из конца вектора в том же масштабе откладывают вектор следующей силы вышеприведенного уравнения сил. Далее продолжают построение с использованием векторов , . Через начало вектора и конец вектора проводим линии по направлениям векторов сил 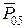и соответственно до их пересечения. Полученный многоугольник является планом сил диады 5-4 (рис. 3.2), на котором обозначены векторы искомых сил 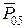и . Направления найденных сил должны быть согласованы с общим направлением векторов сил плана так, чтобы их векторная сумма равнялась нулю. Суммируя векторы и , получим реакцию . 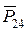Величины реакций (Н) можно определить из выражений

(Н); ,

где 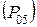, 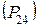– соответствующие отрезки из плана сил, мм.

 

Рис. 3.2. План сил диады 5-4

Определяют реакцию звена 4 на звено 5, т. е. . Векторное уравнение равновесия для сил звена 5 (рис. 3.3) имеет вид

; .

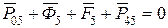Рис. 3.3. Плоская система сил, действующих на звено 5

В приведенном уравнении вектор неизвестен по величине и направлению. Его можно найти, замыкая векторный многоугольник, стороны которого образованы векторами 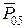, , и искомым вектором . Построение выполняют на плане сил (рис. 3.2).

Величина силы , (Н):

,

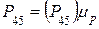где – отрезок из плана сил, мм.

Рассмотрим силовой расчет диады 2-3. Изображаем диаду и плоскую систему сил, ее нагружающую (рис. 3.4).

Рис. 3.4. Плоская система сил, действующих на диаду 2-3

Силы и моменты, нагружающие диаду 2-3: – активная сила; , – силы инерции; , – реакции в шарнирах A и C соответственно; , – нормальная и касательная составляющие реакции ; – момент сил инерции, действующих на звено 2.

Силы инерции , приложены в точках C, B соответственно и направлены противоположно векторам , из плана ускорений соответственно, т. е. векторам и . Момент направлен против ускорения . Вектор силы направлен в противоположную сторону вектора , который изображен на плане сил (рис. 3.2).

Значения сил инерции , и момента сил инерции определяют по следующим формулам:

(Н);

(Н);

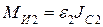(Н×м),

где , – заданные массы звеньев 2 и 3 соответственно, кг; , 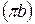– длины отрезков с плана ускорений, мм; – угловое ускорение звена 2, 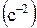, принимаемое из расчетов планов ускорений; – центральный момент инерции звена 2, ,

.

Неизвестную силу определяют из уравнений равновесия в виде моментов сил относительно точки B:

; ,

,

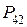где и – плечи сил и соответственно, м. Натуральную величину и определяют с использованием диады 2-3, начерченной в масштабе (рис. 3.4):

; .

Если после вычисления , то действительное направление вектора противоположно указанному на рис. 3.4.

Для определения неизвестных сил , решают графическим путем второе векторное уравнение равновесия сил, для чего строят план сил диады 2-3:

; .

Из произвольной точки “ a ” параллельно вектору силы и в том же направлении откладывают отрезок, который в масштабе изображает величину силы . Далее из конца вектора (точка “ b ”)в том же масштабе откладывают отрезок , параллельный вектору силы . Величины отрезков и определяют по следующим формулам:

; .

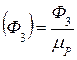Из конца вектора проводят отрезок , параллельный вектору силы , из конца которого в свою очередь отрезок 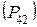, параллельный вектору силы , и далее из конца вектора проводят отрезок параллельно вектору силы . Векторы сил и известны только по направлению, чем пользуются для нахождения их величин следующим образом. Из конца вектора проводят прямую, параллельную направлению вектора , а из начала вектора (точка “ a ”) прямую, параллельную вектору . Точка пересечения двух последних прямых определит положение конца вектора и начало вектора . На рис. 3.5, а изображен план сил диады 2-3.

а)	б)

Рис. 3.5. План сил диады 2-3 (а) и силы, действующие на ползун (б)

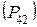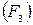Отрезки , , соответствующих сил на плане сил определяют аналогично отрезкам и . Величины искомых сил и определяют по формулам

, ,

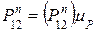где , – длины отрезков из плана сил, мм.

Реакцию шатуна 2 на ползун 3 (рис. 3.5, б) определяют, решая графическим способом следующее уравнение сил:

; .

На рис. 3.5, б направление вектора силы 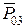соответствует его направлению на плане сил (рис. 3.5, а).

Величину реакции определяют по формуле

,

где – длина отрезка на плана сил, мм.

Рассмотрим силовой расчет начального звена 1. На это звено (рис. 3.6, а) действует реакция со стороны звена 2 и реакция со стороны стойки. Действие силы инерции на звено 1 не учитываем, так как звено 1 уравновешено и центр масс находится в точке О. Момент сил инерции 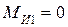, так как звено 1 совершает равномерное вращение () и . В точке A перпендикулярно к звену прикладывают уравновешивающую силу , которая обеспечивает заданный закон движения начального звена механизма.

а)	б)

Рис. 3.6. Силы, действующие на начальное звено 1 (а) и план сил для него (б)

Плоская система сил (рис. 3.6, а) находится в равновесии, и для определения величины уравновешивающей силы достаточно составить уравнение равновесия в виде моментов сил относительно точки O:

; ,

откуда 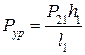(Н),

где – натуральная длина плеча силы , м; 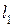– длина звена 1, м.

Реакцию определяют из плана сил (рис. 3.6, б) путем графического решения векторного уравнения

; .

План сил звена 1 строят аналогично вышеприведенным планам сил диад 5-4 и 3-2.

Величину реакции определяют по формуле

,

где – отрезок, изображающий на плане сил (рис. 3.6, б) вектор силы , мм.

4. Условия и варианты домашнего задания.

Условие. Для плоского рычажного механизма провести структурный анализ, построить планы скоростей и ускорений, а также выполнить его кинетостатический анализ ().

Вариант задания. По последней цифре зачетной книжки выбирается схема механизма (рис.0 – рис.9) на стр. 36-38; по предпоследней цифре – вариант числовых значений из таблицы.

 

Варианты числовых данных для расчета механизма

Номер варианта
Исходные данные
Угловая скорость звена 1, ,
Массы звеньев, кг		2,0	2,1	2,2	2,3	2,4	2,5	2,6	2,7	2,8	2,9
	0,4	0,5	0,6	0,7	0,8	0,9	0,95	1,0	1,05	1,1
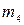
	2,0	2,2	2,5	2,5	2,6	2,6	2,7	2,8	2,9	3,0
	0,4	0,4	0,5	0,5	0,6	0,6	0,7	0,7	0,8	0,8
Длины звеньев, м		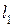0,1	0,11	0,12	0,13	0,14	0,15	0,16	0,17	0,18	0,2
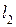
	0,2	0,25	0,3	0,35	0,4	0,4	0,42	0,44	0,46	0,48
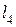
	0,25	0,2	0,2	0,3	0,35	0,3	0,4	0,4	0,45	0,4
Силы, Н
Угол, град	φ

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: