 |
Определение скоростей точек звеньев и угловых скоростей
|
|
|
|
звеньевметодом планов
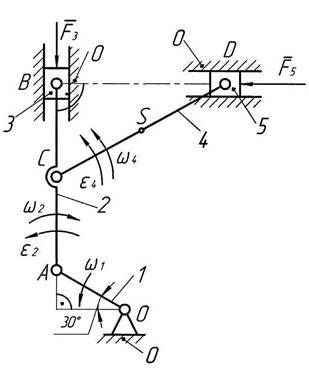
Графические методы определения скоростей и ускорений точек звеньев широко применяются в инженерных расчетах. Их сущность основана на использовании векторных уравнений, связывающих скорости, а также ускорения отдельных точек звеньев механизма с последующим их решением графическим путем. Рассмотрим эти методы на примере механизма, изображенного на рис. 2.1.
Исходные данные для определения скоростей и ускорений точек звеньев механизма: угловая скорость  (
(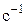 ) звена 1, длины
) звена 1, длины 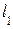 ,
, 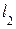 ,
,  (м) звеньев 1, 2, 4,
(м) звеньев 1, 2, 4,  .
.
Составим векторные уравнения, связывающие скорости точек звеньев механизма. Звено AB совершает плоское движение, которое можно разложить на поступательное и вращательное вокруг полюса A. Скорость точки B равна
 ,
,
где 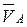 – скорость точки A;
– скорость точки A; 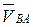 – относительная скорость точки B во вращательном движении вокруг полюса A.
– относительная скорость точки B во вращательном движении вокруг полюса A.
С другой стороны звено 3 движется поступательно относительно стойки и можно записать
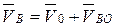 ,
,
где  – скорость стойки (стойка – неподвижная);
– скорость стойки (стойка – неподвижная); 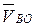 – относительная скорость точки B, направленная по линии движения ползуна (звено 3).
– относительная скорость точки B, направленная по линии движения ползуна (звено 3).
Таким образом, можно записать
 .
.
По аналогии скорость точки D
 .
.
| 
|
| б) | |
| |
| а) | в) |
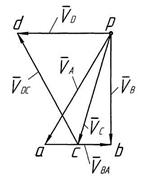
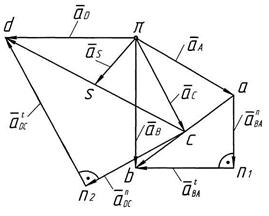
Рис. 2.1. Построение планов: а – кинематическая схема механизма;
б – план скоростей; в – план ускорений
Кроме того  , так как точки C и B расположены на одном звене 2 (
, так как точки C и B расположены на одном звене 2 (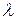 – коэффициент пропорциональности).
– коэффициент пропорциональности).
Запишем составленные векторные уравнения в виде системы:
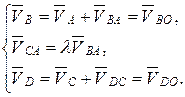 (2.1)
(2.1)
В системе (2.1) векторных уравнений  ,
, 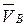 ,
, 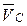 ,
,  – абсолютные скорости точек A, B, C, D звеньев механизма;
– абсолютные скорости точек A, B, C, D звеньев механизма; 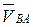 ,
,  ,
,  – скорости точек B, C, D вокруг полюсов A, C. В дальнейшем их будем называть скоростью некоторой точки относительной другой. Например, вектор
– скорости точек B, C, D вокруг полюсов A, C. В дальнейшем их будем называть скоростью некоторой точки относительной другой. Например, вектор 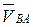 является относительной скоростью точки B по отношению к точке A (для краткости – скорость точки B относительно точки A);
является относительной скоростью точки B по отношению к точке A (для краткости – скорость точки B относительно точки A); 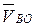 ,
,  – скорости точек B и D относительно стойки 0.
– скорости точек B и D относительно стойки 0.
|
|
|
Уравнения (2.1) позволяют определить скорости рассматриваемых точек механизма. Они могут быть решены графическим методом, который основан на построении планов скоростей.
Метод построения плана скоростей для заданного на рис. 2.1 положения механизма осуществляется в следующем порядке.
1. Вычисляют значение скорости  ,
,  :
:
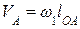 ,
,
где  – угловая скорость начального звена 1,
– угловая скорость начального звена 1, 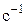 ;
; 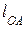 – длина звена 1, м.
– длина звена 1, м.
2. Рассматривают первое векторное равенство системы уравнений (2.1). Принимают во внимание, что вектор 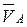 определен ранее, а вектор
определен ранее, а вектор 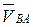 направлен перпендикулярно к оси звена AB в сторону вращения этого звена, т. е. по направлению угловой скорости
направлен перпендикулярно к оси звена AB в сторону вращения этого звена, т. е. по направлению угловой скорости  звена 2. Скорость
звена 2. Скорость  можно записать
можно записать
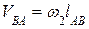 , (2.2)
, (2.2)
где  – угловая скорость второго звена AB,
– угловая скорость второго звена AB, 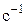 ;
; 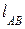 – длина звена 2, м.
– длина звена 2, м.
В формуле (2.2) величина угловой скорости  не известна и подлежит определению, следовательно, на данном этапе неизвестной является величина скорости
не известна и подлежит определению, следовательно, на данном этапе неизвестной является величина скорости  , но как было указано выше известно ее направление – перпендикулярно оси звена AB.
, но как было указано выше известно ее направление – перпендикулярно оси звена AB.
Из первого равенства системы (2.1) следует, что вектор 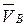 равен вектору
равен вектору 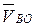 . Величина скорости
. Величина скорости 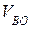 неизвестна, но известно, что звено 3 (ползун) совершает возвратно-поступательные прямолинейные движения по вертикальной линии в направляющих стойки. Поэтому вектор скорости
неизвестна, но известно, что звено 3 (ползун) совершает возвратно-поступательные прямолинейные движения по вертикальной линии в направляющих стойки. Поэтому вектор скорости 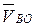 будет направлен также по вертикальной линии, проходящей через точку B.
будет направлен также по вертикальной линии, проходящей через точку B.
3. Строят план скоростей для заданного положения механизма. Из произвольной точки “ p ” (рис. 2.1, б) откладываем определенный отрезок 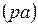 ,перпендикулярный оси звена 1. Считается, что отрезок
,перпендикулярный оси звена 1. Считается, что отрезок 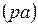 представляет собой вектор скорости
представляет собой вектор скорости 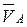 в выбранном масштабе. Вычисляют масштабный коэффициент
в выбранном масштабе. Вычисляют масштабный коэффициент  ,
, 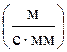 :
:
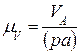 .
.
Отрезок 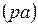 должен быть выбран такого размера, чтобы установленный масштабный коэффициент
должен быть выбран такого размера, чтобы установленный масштабный коэффициент  способствовал удобству вычислений и построений векторов скоростей. Отрезок
способствовал удобству вычислений и построений векторов скоростей. Отрезок 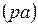 принимают 30…50 мм.
принимают 30…50 мм.
|
|
|
Из точки “ а ” проводят прямую, имеющую направление вектора скоростей 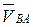 , т. е. перпендикулярную оси звена АВ. Через точку “ p ” проводят прямую параллельную оси движения звена 3 (ползуна). Направление этой прямой соответствует направлению вектора скорости
, т. е. перпендикулярную оси звена АВ. Через точку “ p ” проводят прямую параллельную оси движения звена 3 (ползуна). Направление этой прямой соответствует направлению вектора скорости  . Точка “ b ”пересечения этих прямых определяет конец вектора скорости
. Точка “ b ”пересечения этих прямых определяет конец вектора скорости 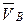 точки B механизма. На плане скоростей скорость
точки B механизма. На плане скоростей скорость 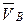 ,
, 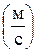 , представлена отрезком
, представлена отрезком  . Величину этой скорости определяют по формуле:
. Величину этой скорости определяют по формуле:
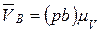 .
.
Полученный при построении треугольник pab называется планом скоростей звена 2, а точка p – полюсом плана скоростей.
При наличии плана скоростей звена всегда можно определить скорость любой точки, принадлежащей этому звену, например, точки C.
Звено 2 относительно точки A совершает вращательное движение, тогда можно записать
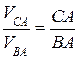 , но
, но 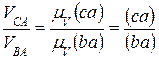 ,
,
где 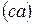 и
и  – отрезки на плане скоростей, соответствующие скоростям
– отрезки на плане скоростей, соответствующие скоростям  и
и  соответственно (точка“ с ”находится на конце вектора скорости
соответственно (точка“ с ”находится на конце вектора скорости  ). Согласно исходных данных
). Согласно исходных данных  , тогда
, тогда
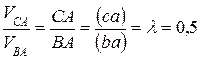 .
.
Таким образом, можно записать
 ,
,
что позволяет определить положение точки “ с ” на плане скоростей путем деления отрезка  на две равные части. Соединяют точку “ p ” с точкой “ с ” и получают графическое изображение вектора скорости
на две равные части. Соединяют точку “ p ” с точкой “ с ” и получают графическое изображение вектора скорости  ,
,  , величину которой определяют по формуле
, величину которой определяют по формуле
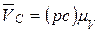 .
.
Для определения скорости  пользуются третьим векторным уравнением системы (2.1).Величина скорости
пользуются третьим векторным уравнением системы (2.1).Величина скорости 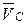 известна, а ее направление показано на плане скоростей (отрезок pc). Вектор скорости
известна, а ее направление показано на плане скоростей (отрезок pc). Вектор скорости 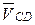 направлен перпендикулярно оси звена 4.Величина скорости
направлен перпендикулярно оси звена 4.Величина скорости 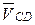 не известна, поэтому из конца вектора
не известна, поэтому из конца вектора 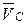 , т. е. из точки “ с ” плана скоростей, проводят линию, перпендикулярную оси звена 4. Далее, величина скорости
, т. е. из точки “ с ” плана скоростей, проводят линию, перпендикулярную оси звена 4. Далее, величина скорости  неизвестна, но известно направление вектора этой скорости – параллельное прямой BD. Из полюса “ p ” плана скоростей проводят прямую параллельную прямой BD. Точка “ d ” пересечение прямой перпендикулярной CD с прямой параллельной BD определяет конец вектора скорости
неизвестна, но известно направление вектора этой скорости – параллельное прямой BD. Из полюса “ p ” плана скоростей проводят прямую параллельную прямой BD. Точка “ d ” пересечение прямой перпендикулярной CD с прямой параллельной BD определяет конец вектора скорости  ,
, 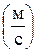 , точки D механизма. Величину этой скорости определяют по формуле
, точки D механизма. Величину этой скорости определяют по формуле
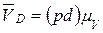 .
.
План скоростей используют для определения угловых скоростей  ,
, 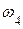
 звеньев 2,4. Можно записать
звеньев 2,4. Можно записать
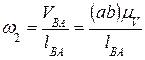 ,
, 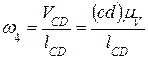 .
.
Направление  определяется следующим образом: мысленно переносят вектор скорости
определяется следующим образом: мысленно переносят вектор скорости 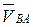 в точку B механизма, сохраняя его направление, ориентируясь на которое, можно определить направление вращения звена BA вокруг точки A – по часовой стрелке. Это и есть направление угловой скорости
в точку B механизма, сохраняя его направление, ориентируясь на которое, можно определить направление вращения звена BA вокруг точки A – по часовой стрелке. Это и есть направление угловой скорости  . Аналогичным образом определяется направление
. Аналогичным образом определяется направление 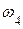 .
.
|
|
|
|
|
|


