 |
Определение ускорений точек звеньев и угловых ускорений
|
|
|
|
звеньев методом планов
Векторы ускорений точек звеньев механизма, схема которого показана на рис. 2.1, связаны между собою следующими зависимостями:
 (2.3)
(2.3)
Построение плана ускорений для заданного на рис. 2.1 положения механизма осуществляется в следующем порядке.
1. Рассматривают первое векторное уравнение системы (2.3) и записывают ускорение точки A для кривошипа (звено 1), вращающегося с постоянной угловой скоростью  :
:
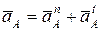 ,
,
где  ,
,  – векторы нормального и касательного (тангенциального) ускорений точки A соответственно. Величины
– векторы нормального и касательного (тангенциального) ускорений точки A соответственно. Величины  и
и 
 определяют по формулам
определяют по формулам
 ;
;
 .
.
Так как  , то
, то  и
и  , для рассматриваемого случая
, для рассматриваемого случая  . Далее из произвольной точки
. Далее из произвольной точки  откладывают отрезок
откладывают отрезок  , представляющий собой в масштабе полное ускорение
, представляющий собой в масштабе полное ускорение  . Направление вектора
. Направление вектора  совпадает с направлением вектора
совпадает с направлением вектора  , т. е. от точки A к точке O.
, т. е. от точки A к точке O.
Отрезок  должен быть выбран таким образом, чтобы масштабный коэффициент
должен быть выбран таким образом, чтобы масштабный коэффициент  обеспечивал удобства вычислений и построений других ускорений и их векторов. Отрезок
обеспечивал удобства вычислений и построений других ускорений и их векторов. Отрезок  принимают 30…50 мм.Его вычисляют следующим образом
принимают 30…50 мм.Его вычисляют следующим образом  :
:
 .
.
Ускорение точки B можно определить графически, используя равенство
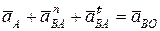 . (2.4)
. (2.4)
Рассмотрим левую часть равенства. Ускорение  известно по величине и направлению (рис. 2.1, в). Вектор
известно по величине и направлению (рис. 2.1, в). Вектор  нормального ускорения точки B относительно точки A известен по величине и направлению (направлен от B к A по оси звена 2). Величина вектора
нормального ускорения точки B относительно точки A известен по величине и направлению (направлен от B к A по оси звена 2). Величина вектора  ,
, 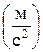
 .
.
Вектор касательного ускорения  точки B по отношению к точке A известен только по направлению – направлен по перпендикуляру к оси звена AB. Его величина
точки B по отношению к точке A известен только по направлению – направлен по перпендикуляру к оси звена AB. Его величина
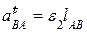
пока не известна, так как  – угловое ускорение звена 2 на данный момент величина не известная.
– угловое ускорение звена 2 на данный момент величина не известная.
Правая часть равенства (2.4) представляет собой ускорение точки B относительно стойки. Его значение не известно, но направление вектора  совпадает с направлением вертикальной линии.
совпадает с направлением вертикальной линии.
|
|
|
Определяют графически ускорение точки B. Из точки “ а ” плана ускорений откладываем отрезок  , равный в масштабе
, равный в масштабе  ускорению
ускорению  . Отрезок проводят параллельно оси звена AB, а его величину (в мм) определяют по формуле
. Отрезок проводят параллельно оси звена AB, а его величину (в мм) определяют по формуле
 .
.
Далее из точки 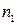 проводят прямую, перпендикулярную оси звена AB. Направление этой прямой совпадает с направлением вектора
проводят прямую, перпендикулярную оси звена AB. Направление этой прямой совпадает с направлением вектора  .
.
Вектор правой части равенства (2.4) известен только по направлению – направлен по вертикальной линии. Из полюса “  ” плана ускорений проводят вертикальную прямую. Пересечение этой прямой и горизонтальной прямой из точки “
” плана ускорений проводят вертикальную прямую. Пересечение этой прямой и горизонтальной прямой из точки “ 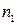 ” дает точку “ b ”, являющуюся концом вектора ускорения точки B, т. е. вектора
” дает точку “ b ”, являющуюся концом вектора ускорения точки B, т. е. вектора  . Его можно вычислить по формуле
. Его можно вычислить по формуле  :
:
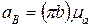 .
.
2. Определяют ускорение точки C звена 2. Конец вектора  ускоренияточки C находится на отрезке
ускоренияточки C находится на отрезке  плана ускорений и точка “ c ” делит этот отрезок в соотношении
плана ускорений и точка “ c ” делит этот отрезок в соотношении  , так как
, так как  . Таким образом,
. Таким образом,  на плане ускорений. Отмечают точку “ c ” на отрезке
на плане ускорений. Отмечают точку “ c ” на отрезке  плана ускорений. Эта точка является концом вектора ускорения
плана ускорений. Эта точка является концом вектора ускорения  точки C звена 2. Его величину,
точки C звена 2. Его величину,  , вычисляют по формуле
, вычисляют по формуле
 .
.
3. Используя третье векторное выражение системы (2.3), определяют ускорение точки D:
 .
.
Ускорение точки C известно по направлению и величине (рис. 2.1, в). Вектор нормального ускорения  направлен от точки D к точке C и его величину,
направлен от точки D к точке C и его величину,  , определяют по формуле
, определяют по формуле
 .
.
Из точки “ c ” на плане ускорений откладывают отрезок  , параллельно оси звена 4. Величину этого отрезка,
, параллельно оси звена 4. Величину этого отрезка,  , определяют по формуле
, определяют по формуле
 .
.
Касательное ускорение  известно по направлению (вектор
известно по направлению (вектор  перпендикулярен оси звена DC), но не известно по величине.
перпендикулярен оси звена DC), но не известно по величине.
Из точки “  ” проводят прямую, перпендикулярную оси звена DC, тем самым обозначая направление вектора
” проводят прямую, перпендикулярную оси звена DC, тем самым обозначая направление вектора  . Из полюса
. Из полюса  плана ускорений проводят прямую, параллельную DB. Пересечение этих двух прямых на плане ускорений даст точку “ d ” – конец вектора ускорения
плана ускорений проводят прямую, параллельную DB. Пересечение этих двух прямых на плане ускорений даст точку “ d ” – конец вектора ускорения  ; его величину
; его величину  определяют по формуле
определяют по формуле
|
|
|
 .
.
Используя план ускорений, определяют ускорения 
 и
и 
 , а затем угловые ускорения
, а затем угловые ускорения 
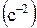 и
и 
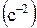 звеньев 2 и 4.
звеньев 2 и 4.
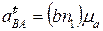 ;
;  ;
;
 ;
;  .
.
Направления  ,
,  определяют аналогично
определяют аналогично  ,
, 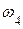 , перенося
, перенося  ,
,  в точки B и D соответственно.
в точки B и D соответственно.
|
|
|


