 |
Давление газа на стенку в МКТ
|
|
|
|
В равновесном состоянии молекулы газа движутся хаотически: все направления движения равновероятны и ни одному из них не может быть отдано предпочтение перед другими. Величина скорости молекул вследствие их многочисленных столкновений может различаться довольно сильно. Однако как очень большие, так и очень малые значения маловероятны. Скорости большинства молекул группируются вблизи некоторого наиболее вероятного значении, близкого к среднему. (Более подробно о характере теплового движения молекул – самостоятельно ).

 Естественно предположить, что давление газа на стенки сосуда обусловлено большим количеством ударов отдельных молекул о стенку. Рассмотрим, как это предположение обосновывается в молекулярно кинетической теории (МКТ).
Естественно предположить, что давление газа на стенки сосуда обусловлено большим количеством ударов отдельных молекул о стенку. Рассмотрим, как это предположение обосновывается в молекулярно кинетической теории (МКТ).
Для упрощения рассуждений предположим, молекулы в газе движутся вдоль трех взаимно перпендикулярных направлений, так что из  молекул в единице объема
молекул в единице объема  часть летит по направлению к элемент
часть летит по направлению к элемент  стенки сосуда.
стенки сосуда.
Выделим мысленно из  молекул в единице объема те
молекул в единице объема те  молекул, скорости которых лежат в интервале от
молекул, скорости которых лежат в интервале от 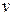 до
до  . За время
. За время  до элемента
до элемента  долетят те молекулы из
долетят те молекулы из  , которые находятся в объеме цилиндра с основанием
, которые находятся в объеме цилиндра с основанием  и высотой
и высотой  , а их скорости направлены к
, а их скорости направлены к  . Следовательно, число ударов этих молекул
. Следовательно, число ударов этих молекул
 . (8.1)
. (8.1)
При соударении со стенкой каждая из молекул передает стенке импульс  , т.к. направление движения изменяется на противоположное. Следовательно, суммарный импульс, переданный элементу поверхности стенки сосуда
, т.к. направление движения изменяется на противоположное. Следовательно, суммарный импульс, переданный элементу поверхности стенки сосуда  за время
за время  молекулами со скоростями в интервале от
молекулами со скоростями в интервале от 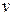 до
до  будет равен:
будет равен:
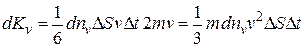 . (8.2)
. (8.2)
Общий импульс, получаемый элементом  стенки от молекул всех скоростей, за
стенки от молекул всех скоростей, за  , мы получим, сложив
, мы получим, сложив  для всех скоростей от 0 до
для всех скоростей от 0 до  (скорость молекул во всяком случае не превосходит скорость света в пустоте):
(скорость молекул во всяком случае не превосходит скорость света в пустоте):
|
|
|
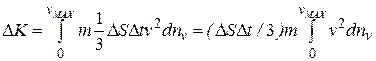 . (8.3)
. (8.3)
Интеграл в (8.3) можно найти, если учесть, что величина
 (8.4)
(8.4)
есть, по определению, среднее значение квадрата скорости. Выразив из (8.4) интеграл и подставив его значение в (8.3), получим:
 (8.5)
(8.5)
Разделив (5) на  , получим по второму закону Ньютона силу давления молекул на
, получим по второму закону Ньютона силу давления молекул на  , а разделив на
, а разделив на  , получим выражение для давления:
, получим выражение для давления:
 (8.6)
(8.6)
где  - среднее значение кинетической энергии поступательного движения молекул.
- среднее значение кинетической энергии поступательного движения молекул.
СРЕДНЯЯ ЭНЕРГИЯ МОЛЕКУЛ
Сравнивая выражение (8.6) для давления и уравнение состояния идеального газа  , приходим к выводу, что
, приходим к выводу, что
 (8.7)
(8.7)
Таким образом, абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекул. Примечательно, что средняя энергия зависит только от температуры и не зависит от массы молекул.
При выводе формулы (6.7) мы учитывали только поступательное движение молекул. Однако молекулы могут участвовать во вращательном движении вокруг центра масс молекулы, а атомы в составе молекул могут совершать колебания относительно ее центра масс. С этими видами движения тоже может быть связана определенная энергия, величину которой определяет положение (закон) о равнораспределении энергии по степеням свободы.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение в системы в пространстве.
Очевидно, что положение в пространстве материальной точки полностью определяется заданием ее трех координат. Следовательно, материальная точка имеет три степени свободы. Система из 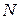 несвязанных материальных точек имеет свойственно
несвязанных материальных точек имеет свойственно  степеней свободы.
степеней свободы.
Каждая жесткая связь между частицами системы устанавливает неизменное расстояние между двумя частицами и уменьшает число степеней свободы на одну. Действительно, зная, пять координат двух точек и расстояние между ними, шестую координату можно вычислить, а в определении говорится о независимых величинах.
|
|
|
 Положение системы из двух жестко связанных материальных точек можно определить, задав три координаты центра масс (радиус-вектором
Положение системы из двух жестко связанных материальных точек можно определить, задав три координаты центра масс (радиус-вектором  ) и два угла
) и два угла  и
и  , которые определяют положение в пространстве оси системы. Координаты центра масс системы изменяются при поступательном перемещении системы, поэтому три из пяти степеней свободы, называют поступательными. Углы
, которые определяют положение в пространстве оси системы. Координаты центра масс системы изменяются при поступательном перемещении системы, поэтому три из пяти степеней свободы, называют поступательными. Углы  и
и  изменяются при повторах системы, поэтому соответствующие две степени свободы называют вращательными. Третья вращательная степень свободы отсутствует, т.к. она соответствует поворотам системы вокруг своей оси, а вращение материальных точек вокруг прямой, проходящей через них лишено по определению смысла.
изменяются при повторах системы, поэтому соответствующие две степени свободы называют вращательными. Третья вращательная степень свободы отсутствует, т.к. она соответствует поворотам системы вокруг своей оси, а вращение материальных точек вокруг прямой, проходящей через них лишено по определению смысла.
 Это ограничение будет снято для системы из трех жестко связанных материальных точек, и такая система будет иметь (
Это ограничение будет снято для системы из трех жестко связанных материальных точек, и такая система будет иметь ( ) шесть степеней свободы: три поступательных и три вращательных. Добавляя к такой системе материальные точки, и жестко связывая каждую из них тремя жесткими связями, мы не изменим количества степеней свободы системы. Следовательно, твердое тело, как система жестко связанных материальных точек имеет шесть степеней свободы,
) шесть степеней свободы: три поступательных и три вращательных. Добавляя к такой системе материальные точки, и жестко связывая каждую из них тремя жесткими связями, мы не изменим количества степеней свободы системы. Следовательно, твердое тело, как система жестко связанных материальных точек имеет шесть степеней свободы,
Рассмотрим систему, состоящую из 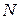 упруго связанных материальных точек (по сути дела модель кристалла!). Такая система будет иметь
упруго связанных материальных точек (по сути дела модель кристалла!). Такая система будет иметь  колебательных степеней свободы, поскольку каждая точка может совершать три независимых колебания, например, вдоль осей декартовой системы координат.
колебательных степеней свободы, поскольку каждая точка может совершать три независимых колебания, например, вдоль осей декартовой системы координат.
Очевидно, что существует равновесная конфигурация точек, которая соответствует минимуму потенциальной энергии системы. Положение этой равновесной конфигурации определяются шестью величинами (сами положения равновесия жестко фиксированы в пространстве!), которым соответствуют три поступательных и три вращательных степени свободы. Остальные 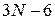 степеней свободы будут, очевидно, колебательными. В реальном кристалле число атомов очень велико, поэтому обычно считают, что атомы кристалла имеют
степеней свободы будут, очевидно, колебательными. В реальном кристалле число атомов очень велико, поэтому обычно считают, что атомы кристалла имеют  степеней свободы.
степеней свободы.
Экспериментально установлено, что при расчете числа степеней свободы молекулы атомы можно считать материальными точками.
|
|
|
При любом устройстве молекулы три из ее степеней свободы будут поступательными. Поскольку все они равноправны, то на каждую из них в соответствии с (8.7) приходится в среднем энергия  .
.
В статистической физике доказывается закон равнораспределения, согласно которому на каждую степень, независимо от ее характера, приходится в среднем одинаковая кинетическая энергия, равная  .
.
Существенным для вычисления средней энергии молекулы является еще одно обстоятельство. В отличие от поступательного и вращательного движений, для которых характерно наличие только кинетической энергии, колебательное движение связано с наличием и кинетической и потенциальной энергии. Вследствие этого колебательные степени свободы обладают вдвое большей энергетической емкостью.
Соответственно среднюю энергию молекулы следует рассчитывать по формуле:
 , (8.8)
, (8.8)
где число степеней свободы  следует находить по формуле:
следует находить по формуле:
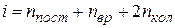 , (8.9)
, (8.9)
Внутренняя энергия моля идеального газа может быть найдена как произведение средней энергии молекулы на число Авогадро:
 , (8.10)
, (8.10)
Соответственно его молярная теплоемкость при постоянном объеме находится по формуле:
 , (8.11)
, (8.11)
а теплоемкость при постоянном давлении, с учетом уравнения Майера, определяется соотношением:
 . (8.12)
. (8.12)
Взяв отношение (8.11) и (8.12), найдем характерное для каждого газа значение отношения теплоемкостей:
 . (8.13)
. (8.13)
Из (8.13) следует, что  определяется количеством и характером степеней свободы молекул газа.
определяется количеством и характером степеней свободы молекул газа.
|
|
|


