 |
Кинетическая энергия при плоском движении
|
|
|
|
Рассмотрим, как вычислить кинетическую энергию тела, если оно одновременно участвует в поступательном и вращательном движении – например, качение колеса по плоскости.
Как мы знаем, при плоском движении тела скорость некоторой точки тела определяется формулой
(4.26)
где 
- скорость поступательного движения точки «0», принятой за начало отсчета для 
,
- радиус-вектор частицы с массой 
по отношению к точке «0». Тогда кинетическая энергия i -той частицы
(4.27)
Учтем, что модуль 
, 
- расстояние i -той точки до оси вращения и, соответственно 
. Воспользовавшись циклической перестановкой сомножителей в смешенном произведении, получим 
.
Тогда из (4.27) получим:
(4.28)
А для кинетической энергии всего тела
(4.29)
Теперь учтем, что
, 
, а 
.
Тогда
(4.30)
Если в качестве «0» взять центр масс, то 
, и
(4.31)
Таким образом, если рассматривать вращение тела относительно оси, проходящей через центр масс, то его кинетическая энергия распадается на два слагаемых. Одно из них описывает кинетическую энергию, обусловленную поступательным движением, другое – вращательным.
ГИРОСКОПЫ.
Гироскопом называют массивное симметричное тело, вращающееся с БОЛЬШОЙ УГЛОВОЙ СКОРОСТЬЮ вокруг оси симметрии.
В этом случае момент импульса гироскопа 
. Если мы будем поворачивать ось гироскопа с некоторой 
в пространстве, то 
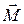, вообще говоря, не совпадает с осью гироскопа. Однако обычно 
и можно считать, что 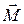направлен по оси гироскопа.
При попытках повернуть ось гироскопа возникает гироскопический эффект: под действием сил, стремящихся повернуть ось гироскопа вокруг оси 
декартовой системы координат, гироскоп поворачивается вокруг оси 
.
Такое поведение объясняется законами динамики вращательного движения. Действительно момент пары сил, 
, 
направленных вдоль , направлен параллельно . Под действием этого момента сил момент импульса гироскопа 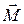за время 
получает приращение 
направленное вдоль 
. Следовательно, ось гироскопа приблизится к направлению – .
|
|
|
Если момент будет продолжать действовать, то ось гироскопа будет поворачиваться, приближаясь к направлению момента сил до тех пор, пока эти направления не совпадут. Дальней шее действие этого момента сил будет приводить только к увеличению момента импульса по модулю.
Гироскопический эффект лежит в основе действия гирокомпаса, который представляет собой гироскоп, точки опоры которого закреплены так, что гироскоп может поворачиваться вокруг вертикальной оси. На раскрученный гироскоп через точки опоры действует момент сил, вовлекающий его в суточное вращение Земли. При длительном воздействии этого момента, ось гироскопа устанавливается параллельно оси вращения Земли, т.е. в меридиональной плоскости, и позволяет определить направление на географический (!) полюс.
Если гироскоп находится в поле силы тяжести и его ось составляет с вертикалью угол 
, то к гироскопу оказывается приложенным момент сил . Он создается силой тяжести 
, которая приложена к центру масс гироскопа и реакцией опоры 
, действующей в точке опоры 
. Раскрученный гироскоп не падает, как «юла»! Поэтому эти силы равны и противоположны по направлению. Момент сил направлен перпендикулярно плоскости, в которой лежат силы и момент импульса 
гироскопа в некоторый исходный момент времени. Если расстояние от точки опоры до центра масс гироскопа равно 
, то модуль этого момента сил
(4.32)
Под действием момента сил момент импульса гироскопа получит приращение 
, а ось гироскопа за 
повернется на угол 
. Следовательно, ось гироскопа будет совершать вращательное движение вокруг вертикали с угловой скоростью:
|
|
|
(4.33)
Такое движение называется прецессией. Соотношение (4.33) дает угловую скорость прецессии. Очевидно, что чем больше момент импульса гироскопа 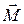, т.е. чем с большей угловой скоростью он вращается вокруг своей оси, тем меньше будет угловая скорость прецессии. (Вспомните процесс остановки «юлы».)
|
|
|
