 |
Определение уравнения состояния. Понятие об идеальном газе. Уравнение состояния идеального газа.
|
|
|
|
Уравнением состояния называют соотношение между параметрами системы, выполняющееся в ходе некоторых процессов.
Простейшими свойствами обладает идеальный газ. С точки зрения молекулярно-кинетической теории идеальным считается газ,
a. молекулы которого не взаимодействуют на расстоянии,
b. столкновения между молекулами происходят абсолютно упруго,
c. суммарный объем молекул пренебрежимо мал по сравнению объемом сосуда, в котором находится газ.
Реальные газы близки по свойствам к идеальному при условиях близких к нормальным: при достаточно высоких температурах и не слишком высоких давлениях (небольшой плотности).
Идеальный газ подчиняется уравнению состояния Клапейрона-Менделеева:
Газовая постоянная. Постоянная Больцмана.
Универсальная газовая постоянная в уравнении Клапейрона-Менделеева
.
Отношение газовой постоянной к числу Авогадро (
) называется постоянной БОЛЬЦМАНА:
Вывод второй формы уравнения состояния.
С использованием постоянной Больцмана уравнению состояния легко придать вид:
ВНУТРЕННЯЯ ЭНЕРГИЯ И
ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА.
Экспериментально установлено, что ВЭ идеального газа зависит только от температуры идеального газа, причем пропорциональна ей:
(7.5)
Это отражает тот факт, что молекулы идеального газа не взаимодействуют друг с другом на расстоянии. В противном случае ВЭ идеального газа должна была бы зависеть от среднего расстояния между молекулами, т.е. от величины, пропорциональной 
.
Теплоемкость тела будем называть величину, равную отношению количества тепла 
, сообщенного телу, к изменению температуры тела 
, обусловленному этим процессом:
|
|
|
(7.6)
Теплоемкость моля вещества называется молярной - 
, единицы массы – 
- удельной. Очевидно, что
(7.7)
Величина теплоемкости зависит от условий, в которых происходит нагревание. Поэтому, различают теплоемкость при постоянном объеме 
и при постоянном давлении 
.
При постоянном объеме - 
- макроскопическая работа не совершается 
, и из первого начала термодинамики следует:
(7.8)
Для моля идеального газа, дифференцируя соотношение (7.6), находим:
(7.9)
Сравнивая соотношения (7.8) и (7.9), приходим к выводу о том, что коэффициент пропорциональности в (7.5) для внутренней энергии одного моля совпадает с удельной теплоемкостью при постоянном объеме, т.е.
(7.10)
Внутренняя энергия произвольной массы 
газа, содержащей 
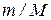молей,
(7.11)
При постоянном давлении нагревание сопровождается увеличением объема и совершением газом работы над внешними телами. Поэтому для нагревания на потребуется
. (7.12)
Соответственно для одного моля, разделив (7.12) на , найдем:
(7.13)
Из уравнения состояния следует, что
. (7.14)
и при постоянном давлении
. (7.15)
Подставив (7.15) в (7.13), получаем
. (7.16)
Соотношение (7.16) называется уравнением Майера. Из него вытекает физический смысл газовой постоянной R: она равна работе, совершаемой одним молем идеального газа при повышении его температуры при постоянном давлении на 1К. Отметим, что 
.
Отношение теплоемкости при постоянном объеме к теплоемкости при постоянном давлении 
является характерной константой для каждого газа, смысл которой мы выясним в дальнейшем. Воспользовавшись уравнением, Майера, найдем, что
. (7.17)
Выразив 
из соотношения (7.17), найдем:
. (7.18)
Тогда для энергии идеального газа справедливы соотношения:
. (7.19)
ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫ.
Обычно рассматривают процессы, в ходе которых газ подчиняется, кроме уравнения состояния, некоторому дополнительному условию. Соответственно различают изотермический, изохорный, изобарный и адиабатный процессы. (Напомним, что адиабатным называется процесс, происходящий без теплообмена с внешней средой.) Оказывается, что все перечисленные процессы являются частичными случаями политропического процесса, в ходе которого, по определению, остается постоянной теплоемкость тела.
|
|
|
Найдем уравнение политропы, т.е. уравнение, связывающие параметры идеального газа при политропическом процессе. Обозначим теплоемкость тела в ходе конкретного политропического процесса . Тогда из первого начала термодинамики 
следует, что (
)
. (7.20)
Преобразуем (7.20) к виду:
. (7.21)
Выразим 
из уравнения состояния:
, (7.22)
и подставим в (7.21):
. (7.23)
Умножим (7.23) на 
и перегруппируем слагаемые:
. (7.24)
Разделим (7.24) на 
и учтем что 
:
. (7.25)
После интегрирования (7.25) получим соотношение:
. (7.26)
Разделим обе части (7.26) на 
:
. (7.27)
Обозначим:
. (7.28)
Тогда (7.27) можно записать в виде
или 
. (7.29)
Потенцирование (7.29) (надо возвести число е в степень выражения в левой части) дает соотношение:
. (7.30)
Уравнение (7.30) есть искомое уравнение политропы, а величина n называется показателем политропы.
Значение 
соответствует 
, т.е. изобарному процессу.
Значение 
соответствует нулевому знаменателю в (7.28), т.е. 
, а значит изохорному процессу.
Значение 
соответствует закону Бойля-Мариотта, т.е. изотермическому процессу. Действительно, при изотермическом процессе 
по определению процесса, а сообщаемое тепло 
. Следовательно, теплоемкость при изотермическом процессе 
, что соответствует .
При адиабатном процессе 
при 
, а значит теплоемкость в ходе такого процесса 
. В этом случае показатель политропы оказывается равным 
и, следовательно, уравнение адиабаты имеет вид:
. (7.31)
Уравнение адиабаты (7.31) называется уравнением Пуассона. Это уравнение описывает обратимый адиабатный процесс (конкретные точные значения параметров), а значит процесс квазистатический. Поскольку в природе не существует не проводящих тепло тел, то достаточно близкими к адиабатному могут быть только весьма быстро протекающие процессы. Примером такого процесса может быть сжатие и расширение, происходящее в данной точке газа при распространении в нем звуковой волны. При этом состояние газа в малом объеме приближается к равновесному, и при распространении волны в газе происходит адиабатный процесс.
|
|
|
|
|
|
