 |
Диполь во внешнем электрическом поле
|
|
|
|
В однородном электрическом поле на диполь действуют силы 
и 
, которые образуют пару сил с моментом:
(12.39) Этот момент устанавливает диполь электрическим моментом по направлению электрического поля.
Рассмотрим диполь в неоднородном поле, симметричном относительно оси 
, на которой находится диполь. Потенциальная энергия диполя
(12.40)
Считая диполь достаточно малым, приращение потенциала на отрезке 
можно представить в виде:
(12.41)
Тогда для потенциальной энергии получаем:
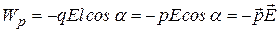(12.42) В неоднородном поле силы, действующие на заряды диполя неравны, и на диполь действует результирующая сила, направленная вдоль оси ох, наряду с вращательным моментом. Эту силу можно найти по общему правилу 
.
Поскольку поле изменяется только по оси , то для точек оси производные по 
и 
равны нулю, и для силы, действующей на диполь, получаем:
(12.43)
При 
сила (12.43) положительна, и это означает, что диполь втягивается в область более сильного поля. При 
диполь выталкивается в область более слабого поля.
Однако, учитывая ориентирующие действие поля, стремящееся установить диполи по направлению поля, можно утверждать, что если диполь не закреплен, и его ориентация может измениться, то на диполь будет действовать результирующая сила, втягивающая его в область более сильного поля. Этот вывод справедлив и в общем случае при произвольной неоднородности поля.
Описание свойств векторных полей
Материальный аппарат теории поля – векторный анализ. Будем говорить, что нам задано поле некоторой величины, если во всех точках рассматриваемого объема нам задано значение этой величины. Если в каждой точке 
пространства или некоторой среды задана скалярная функция 
, то говорят, что задано скалярное поле. Если величина векторная, то говорят, что задано векторное поле.
|
|
|
Градиент
По определению градиентом скалярной функции 
называется вектор
. (13.01)
Следует помнить о том, что градиента векторной функции не существует, в силу того, что он просто не определен. Можно рассматривать градиент модуля вектора, но модуль – это скалярная величина.
Физический смысл градиента функции заключается в том, что это вектор, направленный в сторону скорейшего возрастания функции, а по модулю равный производной, взятой вдоль направления скорейшего возрастания.
НАПРИМЕР, если в стакан налит кипяток, то, очевидно, что в стенках стакана устанавливается градиент температуры. Поскольку градиент направлен в сторону скорейшего возрастания величины, то градиент температуры перпендикулярен стенкам стакана. Температура изменяется и вдоль направления черной стрелки, но направление СКОРЕЙШЕГО возрастания задается, очевидно, красной.
Величину градиента грубо можно оценить, разделив известное изменение величины на расстояние на котором оно происходит, если это расстояние в направлении скорейшего изменения.
Пока стенки не прогрелись по толщине, можно считать, что на внутренней поверхности температура 100 0С, а на внешней – в соответствии с температурой окружающей среды – 20 0С. Если толщина стенок 1 мм, то градиент по модулю равен 80 0С/мм = 8 104 0С/м. По мере прогревания стенок температура воды в стакане немного упадет, но на внешней поверхности – сильно возрастет. Разница температур уменьшится и градиент по модулю тоже.
Сравним понятия градиент и скорость. Когда мы говорим «скорость изменения некоторой величины равна…», то обычно подразумеваем, что речь о быстроте изменения величины во времени. Говоря о том, что градиент некоторой величины составляет столько-то, мы говорим о быстроте изменения величины в пространстве, т.е. при изменении пространственных координат.
|
|
|
1. Поток вектора
Понятие векторного анализа наиболее наглядны при рассмотрении поля вектора скорости текущей жидкости. Собственно они и возникли в процессе развития гидродинамики, и этим обусловлена терминология, используемая в векторном анализе.
Рассмотрим течение идеальной жидкости, т.е. жидкости несжимаемой, молекулы которой взаимодействуют абсолютно упруго.
По определению, объемжидкости, протекающий в единицу времени через некоторую воображаемую поверхность называется потоком жидкости через S. Пусть скорость направленного движения частиц жидкости, пересекающих поверхность 
, равна 
. Выделим мысленно на поверхности элемент 
и будем считать, что он настолько мал, что в его пределах скорость направленного движения частиц жидкости одинакова. Ориентацию в пространстве этого элемента зададим ортом нормали к нему 
. За время 
через пройдет жидкость, заключенная в объеме
(13.02)
Следовательно, по определению потока, элементарный поток через :
(13.03)
Устремив размеры элемента поверхности к нулю ( → 0), получим соотношение:
(13.04)
Формула (13.04) в соответствии с определением скалярного произведения векторов эквивалентна следующим:
. (13.06)
Тогда поток жидкости через всю поверхность должен определяться соотношением:
(13.07)
Распространив этот подход на все векторные поля, можем сформулировать определение потока произвольного вектора 
через поверхность :
(13.08)
Основные свойства потока вектора: скалярная алгебраическая величина, знак которой зависит от выбора направления нормали к .
В случае замкнутых поверхностей всегда используется внешняя нормаль.
|
|
|
