 |
Геометрическая интерпретация потока
|
|
|
|
Поле всякого вектора  можно задать с помощью линий, аналогичных силовым линиям
можно задать с помощью линий, аналогичных силовым линиям  . Представление поля с помощью линий вектора является весьма неточным, но очень полезно для наглядного представления о поле. В рамках этого представления потоку вектора можно придать очень наглядную геометрическую интерпретацию. При этом будем предполагать, что количество линий вектора достаточно для представления модуля вектора с заданной точностью.
. Представление поля с помощью линий вектора является весьма неточным, но очень полезно для наглядного представления о поле. В рамках этого представления потоку вектора можно придать очень наглядную геометрическую интерпретацию. При этом будем предполагать, что количество линий вектора достаточно для представления модуля вектора с заданной точностью.
 Для плоского элемента поверхности
Для плоского элемента поверхности  , нормаль к которому образует угол
, нормаль к которому образует угол  c вектором
c вектором  , число пересечений
, число пересечений  линий вектора
линий вектора  с
с  равно произведению густоты линий (т.е. модуля вектора) на площадь
равно произведению густоты линий (т.е. модуля вектора) на площадь 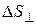 площадки, расположенной перпендикулярно силовым линиям в данной точке пространства. Очевидно, что количество линий, пересекающих
площадки, расположенной перпендикулярно силовым линиям в данной точке пространства. Очевидно, что количество линий, пересекающих 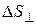 и
и  одинаково, а площади связаны соотношением:
одинаково, а площади связаны соотношением:
 . (13.09)
. (13.09)
Поэтому
 (13.10)
(13.10)
Поток вектора выражается таким же соотношением. Поэтому можно утверждать, что поток вектора через некоторую поверхность численно равен количеству пересечений линий вектора с этой поверхностью:
 (13.11)
(13.11)
Необходимо, однако, учесть, что поток – величина алгебраическая. Если на рисунке 13.2 направление линий вектора изменить на противоположное, то поток станет отрицательным. Для совпадения знаков  и
и  пересечения с острым углом
пересечения с острым углом  считают положительными, а с тупым
считают положительными, а с тупым  – отрицательными.
– отрицательными.
Большое значение имеет рассмотрение потока вектора через замкнутую поверхность. Для замкнутых поверхностей положительной считается внешняя нормаль  и с «+» берутся пересечения, связанные с выходом наружу линий вектора. Пересечения при входе внутрь берутся с « – ».
и с «+» берутся пересечения, связанные с выходом наружу линий вектора. Пересечения при входе внутрь берутся с « – ».

 Обратим внимание на то, что если линии вектора непрерывны внутри поверхности, то каждая линия пересекает поверхность четное число раз: половину с «+», половину с « – » и, соответственно поток через поверхность оказывается равным нулю.
Обратим внимание на то, что если линии вектора непрерывны внутри поверхности, то каждая линия пересекает поверхность четное число раз: половину с «+», половину с « – » и, соответственно поток через поверхность оказывается равным нулю.
|
|
|
Если же линии обрываются или начинаются внутри S, то поток через S

|
Дивергенция вектора
Вернемся к рассмотрению течения жидкости и поля вектора скорости  частиц жидкости. Представим в окрестности некоторой точки
частиц жидкости. Представим в окрестности некоторой точки 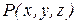 воображаемую з амкнутую поверхность
воображаемую з амкнутую поверхность  , ограничивающую объем
, ограничивающую объем  . Если внутри
. Если внутри  в объеме
в объеме  жидкость не исчезает и не появляется, то линии вектора
жидкость не исчезает и не появляется, то линии вектора  (они же линии тока жидкости) непрерывны, и
(они же линии тока жидкости) непрерывны, и  .
.
Если  , то это означает, что внутри
, то это означает, что внутри  есть источники, мощность которых равна
есть источники, мощность которых равна  (стоки рассматриваем как источники с отрицательной мощностью). Под мощностью источника подразумевается объем жидкости, выбрасываемый им в единицу времени. Отношение
(стоки рассматриваем как источники с отрицательной мощностью). Под мощностью источника подразумевается объем жидкости, выбрасываемый им в единицу времени. Отношение  есть средняя удельная мощность источников в
есть средняя удельная мощность источников в  .
.
Поток вектора  через поверхность
через поверхность  и средняя удельная мощность источников в объеме
и средняя удельная мощность источников в объеме  интегрально, по объему
интегрально, по объему  , характеризует характер изменения поля и поведение вектора скорости частиц. Однако очень часто возникает необходимость более детального описания поведения поля вектора скорости, например интенсивности возникновения новых линий вектора в зависимости от координат. С этой целью естественно уменьшить мысленно объем
, характеризует характер изменения поля и поведение вектора скорости частиц. Однако очень часто возникает необходимость более детального описания поведения поля вектора скорости, например интенсивности возникновения новых линий вектора в зависимости от координат. С этой целью естественно уменьшить мысленно объем  . По определению предел отношения потока вектора
. По определению предел отношения потока вектора  через замкнутую поверхность, ограничивающую некоторый объем в окрестности заданной точки поля, к величине объема
через замкнутую поверхность, ограничивающую некоторый объем в окрестности заданной точки поля, к величине объема  , при его стремлении к нулю, называют дивергенцией соответствующего вектора:
, при его стремлении к нулю, называют дивергенцией соответствующего вектора:
|
|
|
 (13.12)
(13.12)
(можно говорить о пределе удельной мощности источников вектора).
Соответственно, по определению, для произвольного вектора  дивергенцией называется величина
дивергенцией называется величина
 (13.13)
(13.13)
Геометрическая интерпретация потока вектора, как количества пересечений линий вектора с поверхностью, позволяет истолковать дивергенцию вектора  , как функцию, равную плотности точек, в которых начинаются линии
, как функцию, равную плотности точек, в которых начинаются линии  . В точках, где линии вектора заканчиваются дивергенция вектора отрицательна.
. В точках, где линии вектора заканчиваются дивергенция вектора отрицательна.
По смыслу  характеризует распределение в пространстве источников силовых линий и определяет плотность мощности источников вектора. Произведение
характеризует распределение в пространстве источников силовых линий и определяет плотность мощности источников вектора. Произведение  дает мощность источников в объеме
дает мощность источников в объеме  .
.
Такое определение дивергенции не зависит от выбора системы координат, однако, неудобно для вычислений.
13.4 Выражение для  в декартовой системе координат
в декартовой системе координат
 Возьмем в окрестности точки
Возьмем в окрестности точки 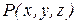 бесконечно малый объем
бесконечно малый объем  в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат величиной
в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат величиной  соответственно. Очевидно, что
соответственно. Очевидно, что 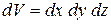 .
.
Найдем поток через поверхность, ограничивающую  . Для смотрящей на нас грани параллелепипеда единичная внешняя нормаль
. Для смотрящей на нас грани параллелепипеда единичная внешняя нормаль  совпадает с направлением оси
совпадает с направлением оси  . Поэтому проекция вектора на направление нормали к этой грани
. Поэтому проекция вектора на направление нормали к этой грани
 , (13.14)
, (13.14)
где  проекция вектора
проекция вектора  на ось
на ось  .
.
Для противоположной грани:
 , (13.15)
, (13.15)
Поскольку орт нормали  направлен навстречу оси
направлен навстречу оси  . Тогда суммарный поток вектора
. Тогда суммарный поток вектора  через грани, перпендикулярные оси
через грани, перпендикулярные оси  :
:
 . (13.16)
. (13.16)
Изменение проекции  на ось
на ось  можно найти в виде:
можно найти в виде:
 . (13.17)
. (13.17)
Поэтому поток через две грани
 . (13.18)
. (13.18)
Рассуждая аналогичным образом, для граней перпендикулярных двум другим осям системы координат, можно найти значения потоков:
 и
и  . (13.19)
. (13.19)
Тогда поток через всю поверхность параллелепипеда
 . (13.20)
. (13.20)
Поэтому дивергенцию вектора в декартовой системе координат можно найти, воспользовавшись соотношением:
 . (13.21)
. (13.21)
|
|
|


