 |
Раздел 2. Статика атмосферы
|
|
|
|
Уравнение статики атмосферы выражает условия равновесия двух сил: вертикального градиента давления и силы тяжести и позволяет определить изменения давления с высотой в зависимости от плотности воздух
где ρ – плотность воздуха (кг/м3), g – ускорение свободного падения, которое можно считать при описании процессов на высотах z < 100 км и для данной точки земной поверхности величиной постоянной.
В дифференциальной форме уравнение статики позволяет выполнять расчёты изменения давления для малых приращений dz. Если известен закон изменения с высотой плотности или температуры, уравнение статики может быть проинтегрировано. Интегралы основного уравнения статики, полученные при различных предположениях относительно изменения температуры и плотности воздуха с высотой называются барометрическими формулами. Вид их различен в зависимости от вида функций T = T(z) и ρ = ρ(z)
1) при постоянной плотности (однородная атмосфера)
,
,
,
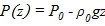где Rс – удельная газовая постоянная сухого воздуха;
2) при постоянной температуре (изотермическая атмосфера)
,
,
,
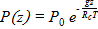3) при постоянном температурном градиенте (политропная атмосфера)
,
,
,
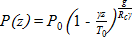где γ – градиент температуры;
4) при произвольном изменении температуры с высотой (общий случай)
,
,
,
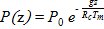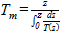где Tm – средняя барометрическая температура.
Для точных расчётов высоты и давления в реальной атмосфере используется полная барометрическая формула (формула Лапласа).
,
где z - z 1 – разность высот в м; tср – среднеарифметическая температура слоя воздуха между уровнями z и z 1; 
– среднеарифметическое отношение упругости пара, содержащегося в воздухе, к атмосферному давлению; φ – широта места; zср – средний уровень в слое; C 1, C 2, C 3, C 4 – постоянные (C 1 = 0,0036 град-1; C 2 = 0,378; C 3 = 0,00264; C 4 = 3,14·10-7 м).
|
|
|
Для расчетов с точностью до 1% вычисления можно производить по сокращенной барометрической формуле:
.
Абсолютной высотой (абсолютным геопотенциалом) изобарической поверхности называют геопотенциальную высоту изобарической поверхности над уровнем моря. Измеряется в геопотенциальных метрах (гп·м) и определяется формулой
,
где Р 0, Р – давление на уровне моря и на заданной изобарической поверхности;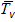 
– средняя виртуальная температура слоя между уровнями Р 0 и Р.
Приращение абсолютного геопотенциала δΦP в результате изменения P 0 (δP 0 ) и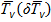 
равно
Относительной высотой одной изобарической поверхности над другой (относительным геопотенциалом) называется толщина слоя в геопотенциальных метрах между этими изобарическими поверхностями (разность их абсолютных геопотенциалов). Относительный геопотенциал в геопотенциальных метрах определяется формулой
где P 1 и P 2 – давление на нижней и верхней изобарических поверхностях,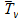 
– средняя виртуальная температура слоя между этими поверхностями.
Приращение относительного геопотенгдиала 
в результате изменения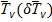 
определяется по формуле
ЗАДАЧИ
2.1. Определить величину, вертикального градиента давления при нормальных условиях вблизи уровня моря (ρ = 1,29·10-3 г/см3). Как изменяется вертикальный градиент давления с высотой и чем это объясняется? Схематически изобразить изменение давления с высотой в однородной атмосфере. В однородной или в реальной атмосфере давление изменяется быстрее? Для однородной атмосферы, в которой температура у поверхности Земли равна 25°C найти уровни, где давление обращается в нуль и где оно вдвое меньше давления у поверхности.
2.2. Объяснить, почему на высотах в холодных воздушных массах преобладает низкое давление, а в тёплых – высокое. В каких широтах – низких или высоких – давление быстрее изменяется с высотой при прочих равных условиях? Вычислить давление на уровнях 1, 5, 8 км для однородной атмосферы. Р 0 = 1000 гПа; T 0 = 273 K
|
|
|
2.3. Вычислить высоту однородной атмосферы при t = –25°C и t = 25°C. Как и на сколько изменится высота однородной атмосферы при изменении температуры у поверхности Земли от 0°С до 10°С, 20°С, 30°С? Проанализировать сезонный ход высоты однородной атмосферы.
2.4. Определить вертикальный градиент температуры в однородной атмосфере. Найти температуру на высотах 3, 5, 7 км. Температуру у поверхности Земли принять равной 10,0°С. Схематически изобразить изменение температуры с высотой.
2.5. Какова высота изотермической атмосферы? Вычислить давление на уровнях 1, 3, 5, 7 км для однородной и изотермической атмосферы. Давление у поверхности Земли принять равным 1000 гПа, температуру 0,0°С. В какой атмосфере давление быстрее убывает с высотой?
2.6. Определить изменение давления в изотермической атмосфере в слое 0–5 км, 5–10 км, 20–25 км.
2.7. Барометрической ступенью называется такая высота, на которую нужно подняться с исходного уровня, чтобы давление упало на 1 гПа (или 1 мм рт.ст.). Вычислить величину барометрической ступени в теплой (t = 20,0°С) и холодной (t = –20,0°С) воздушных массах. Давление на исходном уровне принять равным 1000 гПа. Сравнить их величину.
2.8. Вывести формулу для изменения барометрической ступени в зависимости от изменения давления и температуры, считая эти изменения малыми. Каково относительное изменения барометрической ступени (в %), если:
а) температура повысится на 1°C;
б) температура понизится на 1°C;
в) давление повысится на 1 гПа;
г) давление понизится на 1 гПа.
Т = 250 K, Р = 500 гПа.
2.9. Определить высоту политропной атмосферы, если температура на уровне моря 15,0°C, а вертикальный градиент температуры 6, 10, 15 K/км.
2.10. При каких значениях вертикального градиента формула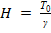 
теряет физический смысл? Отличается ли высота реальной атмосферы от высоты политропной атмосферы с градиентом 6 K/км?
2.11. Используя барометрическую формулу, вывести формулу, связывающую между собой локальные изменения давления на разных уровнях в изотермической атмосфере.
2.12. Найти по сокращенной барометрической формуле высоты, на которых атмосферное давление в 5 и 10 раз меньше, чем на уровне моря. Среднюю температуру тропосферы считать равной –5,0°С.
|
|
|
2.13. Определить с точностью до 1% давление на высоте 10 км в стандартной атмосфере, в которой на уровне моря принято давление 1000 гПа и температура 15,0°С. Изменился бы результат расчётов, если бы в атмосфере наблюдалась инверсия температуры?
2.14. В двух соседних воздушных массах, имеющих разную температуру у поверхности Земли, давление одинаково и равно 1000 гПа. Какова разность давлений на высоте 1000 м, если температура одной воздушной массы T 1 = T 0 - γ 1 z, другой T 2 = T 0' - γ 2 z, γ 1 = 0,5 K/100 м, γ 2 = 0,1 K/100 м, Т 0 = 270 K, T 0' = 275 K?
2.15. Вычислить абсолютную высоту изобарических поверхностей 900, 800, 700, 600, 500, 400, 300, 200 и 100 мб для однородной атмосферы, если 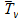= 300 K, P 0 = 1000 мб.
2.16. Каково изменение температуры 
, если при изменении давления на уровне моря δP 0 = 5 мб изобарическая поверхность 500 мб поднялась на δΦP – 50 гп м?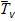 
= 260 K, P 0 = 1000 мб?
2.17. Как должно измениться давление на уровне моря, если при превышении средней температуры на 3°C изобарическая поверхность 500 гПа поднялась на 30 гп м? 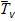= 265 K, давление над уровнем моря Р 0 = 1000 гПа.
2.18. Как должно измениться давление на уровне моря, если при понижении средней температуры на 4°C изобарическая поверхность 600 мб опустилась на 25 гп м? 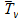= 260 K, P 0 = 990 мб.
2.19. На сколько геопотенциальных метров должна измениться высота изобарической поверхности 400 мб, если при повышении средней температуры на 5°C давление на уровне моря уменьшилось на 7 мб? 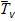= 285 K, Р 0= 1000 мб.
2.20. На сколько процентов и как изменится геопотенциальная Φ 700 и Φ 200, если:
- давление на уровне моря изменится от 1000 до 975 мб при неизменной средней температуре;
- средняя температура слоя изменится от –3°C до –13°C при неизменном давлении на уровне моря.
2.21. Вычислить относительный геопотенциал по следующим данным:
а) P 1 = 300 мб, Р 2 = 200 мб,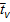 
= –33°C,
б) Р 1 = 1000 мб, P 2 = 100 мб, 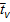= –38°C.
2.22. Температура на уровне 1000 мб равна –5°C, вертикальный градиент температуры γ = 6,5 K/км. Чему равен относительный геопотенциал 
?
|
|
|
2.23.Чему равна средняя температура слоя между поверхностями 700 мб и 500 мб, если его толщина составляет 2,5 км?
|
|
|
