Главная | Обратная связь | Поможем написать вашу работу!

Динамические процессы в пограничном и приземном слоях атмосферы. Волны в атмосфере.

Примером движений идеальной жидкости являются ветры в свободной атмосфере.

Прямолинейное равномерное движение воздуха под действием силы Кориолиса и горизонтального градиента давления называется геострофическим ветром. Геострофический ветер направлен по касательной к изобаре так, что в северном полушарии область низких давлений остается слева по ходу движения, а в южном – справа. Проекции, скорости геострофического ветра определяются по формулам:

где ρ – плотность воздуха, l = 2 ·ω·sinφ – параметр Кориолиса, ω – угловая скорость суточного вращения Земли.

Термическим ветром в некотором слое называется векторная разность геострофического ветра на верхней и нижней границах этого слоя. Термический ветер направлен по касательной к изотерме средней температуры слоя так, что в северном полушарии область низких температур остается от него слева, а в южном – справа. Проекции скорости термического ветра определяются по формулам:

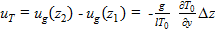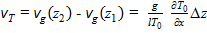где u_g, v_g – проекции скорости геострофического ветра на высоте z ₂ и z ₁; g – ускорение свободного падения, T ₀ – средняя температура слоя; Δ z – толщина слоя.

Разность между действительным ветром в свободной атмосфере и геострофическим ветром называется агеострофическим отклонением. Модуль скорости агеострофического отклонения определяется по формуле:

где – скорость реального ветра.

Агеострофическое отклонение и направлено влево от в северном полушарии.

Градиентным ветром называется установившееся движение воздуха по стационарным круговым траекториям при отсутствии трения. Градиентный ветер направлен по касательной к изобаре так, что область меньших давлений остается в северном полушарии слева от движения, а в южном – справа.

Скорость градиентного ветра определяется по формуле:

где r – радиус круговой траектории.

В северном полушарий (l > 0) в циклонах ( > 0), w_r – положительная величина, т.е. скорость направлена против часовой стрелки. В антициклоническом поле ( < 0), w_r < 0, т.е. движение происходит по часовой стрелке.

Пограничным слоем атмосферы называется слой, в котором наряду с градиентом давления и кориолисовой силой существенную роль играют силы турбулентного трения.

Если ускорение отсутствует, вектор горизонтального градиента давления не меняется с высотой и коэффициент турбулентности постоянен, то распределение ветра с высотой z в пограничном слое атмосферы даётся формулами:

u = u_g (1 – e^–mz cos mz),

v = u_g e^–mz sin mz,

где u – составляющая скорости ветра вдоль геострофического ветра у поверхности Земли; v – составляющая, перпендикулярная геострофическому ветру у поверхности Земли (в северном полушарии направлена влево), u_g – скорость геострофического ветра у земли

где ω – угловая скорость суточного вращения Земли, φ – географическая широта места, k – коэффициент турбулентности. Кривая изменения вектора скорости ветра с высотой v = f(u), называется спиралью Экмана. Верхняя граница пограничного слоя находится по формуле:

Слой вблизи поверхности Земли (толщиной около 10 - 100 м) называется приземным слоем. Важной особенностью приземного слоя является относительное постоянство по высоте турбулентных потоков количества движения, тепла и влаги.

Важное значение при рассмотрении вопроса о распределении физических параметров и характеристик турбулентности вблизи поверхности Земли имеет критерий L (L – масштаб Монина-Обухова), имеющий размерность длины

где скорость трения, τ – касательное напряжение у земной поверхности, ρ – плотность воздуха, C_P – теплоёмкость воздуха при постоянном давлении, g – ускорение свободного падения, T – температура воздуха, Q ₀ – вертикальный турбулентный поток тепла в приземном слое или у поверхности Земли.

При безразличной стратификации, т.е. при отсутствии вертикального турбулентного потока тепла (Q ₀ = 0, L = ∞) скорость ветра w в приземном слое атмосферы меняется с высотой по логарифмическому закону:

где ϰ = 0,4 – постоянная Кармана, z ₀ – уровень шероховатости, т.е. высота, на которой скорость ветра у поверхности Земли обращается в нуль. Удельная влажность при безразличной стратификации меняется по следующей формуле:

где G – скорость испарения, , k_q – коэффициент турбулентной диффузии водяного пара.

Коэффициент турбулентности при безразличной стратификации линейно изменяется с высотой, для z ≥ z ₀

k = ϰ z.

При стратификации, близкой к безразличной, турбулентный поток тепла Q ₀ мал (а значит мало ), скорость ветра, температура и удельная влажность меняются с высотой в приземном слое следующим образом:

коэффициент В – меняется в широких пределах 0,6 ≤ В ≤ 10, , k_T – коэффициент турбулентной температуропроводности. Считается, что α_T близко к единице при безразличной стратификации, увеличивается до 3,0 – 3,5 с ростом неустойчивости и меньше единицы при устойчивой стратификации, причем α_T = α_s.

Коэффициент турбулентности при стратификации, близкой к безразличной, меняется по формуле:

При неустойчивой стратификации (L < 0) коэффициент турбулентности больше, чем при устойчивой (L > 0).

Важную роль в процессах энергообмена в природной среде играют волновые, процессы в атмосфере. Специфические формы облаков делают видимыми волны в атмосфере.

Характеристики волн – длина волны λ, волновое число к, период Т, частота ν, фазовая скорость (скорость распространения волн) c и групповая скорость c_гр связаны между собой соотношениями:

, , , .

В спокойной устойчиво стратифицированной атмосфере воздушная частица стабильно связана со своим положением равновесия. Если внешние силы выведут её из этого положения равновесия, то разность плотностей между частицей и средой приведет к появлению архимедовой силы, которая будет стремиться вернуть частицу обратно. Вследствие полученного импульса, частица пройдет положение равновесия и будет колебаться около среднего положения, пока её энергия не диссипирует. Волны, возникающие при такого рода движениях, называются внутренними гравитационными волнами. Важной характеристикой устойчивой стратификации атмосферы является частота Вяйсяля-Брента, которая имеет смысл частоты инерционных колебаний частиц жидкости или газа, адиабатически смещенных по вертикали от уровня соответствующего положению равновесия:

Амплитуда гравитационных волн равна , где c₀ – фазовая скорость волн в начальный момент (на начальном уровне).

Под влиянием возмущений и вращения Земли в западном потоке возникают волновые движения, получившие название волн Россби. Скорость движения волн Россби c равна

где u – скорость западного переноса, λ – длина волны, β = (2 ω cos φ)/ R_З – параметр Россби, R_З – радиус Земли. Скорость движения волн с запада на восток тем меньше, чем больше длина волны. Волны с длиной λ_s, удовлетворяющей соотношению

неподвижны (c = 0). Волны, длина которых λ > λ_s движутся с востока на запад. Длина неподвижных волн может составлять несколько тысяч километров.

ЗАДАЧИ

5.1. При смещении вдоль меридиана в северном полушарии от искомой точки на 3° широты к северу давление возросло на 0,5%. Геострофический ветер на этой широте 12 м/с, а температура в свободной атмосфере равна –6,5°С. Определить широту точки.

5.2. Вычислить скорость геострофического ветра на уровне моря, если расстояние между соседними изобарами на карте масштаба 1:10⁷ равно 3 см, широта места φ = 60°, при стандартном значении плотности воздуха, равном 1,29 кг/м³.

5.3. Ветер на высоте 1,5 км северный 12 м/с, средний горизонтальный градиент температуры в слое 1,5 км до 2,5 км равен 2°С/100 км и направлен на юг. Определить скорость геострофического ветра на высоте 2,5 км, если широта места 60°, T ₀ = 283 K.

5.4. Определить средний горизонтальный градиент температуры, если известно, что на станции, широта которой 50°, геострофический ветер на высоте 700 м равен 8 м/с, а на высоте 1400 м скорость геострофического ветра обращается в нуль, T ₀ = 273 K.

5.5. Скорость реального ветра равна 12 м/с на широте 55°. Известно, что геострофический ветер отклонен вправо на 45° от реального ветра, а его скорость равна 9,5 м/с. Определить, как направлено и чему равно ускорение движения воздушного потока.

5.6. Определить скорость ветра в циклоне на широте 60°, на расстоянии 500 км от центра циклона, если давление на круговой траектории радиуса 600 км равно 99 гПа, а на круговой траектории радиуса 400 км равно 98,5 гПа.

5.7. Определить скорость ветра в антициклоне на широте 50°, если известно, что расстояние между соседними изобарами на карте масштаба 1:10⁷ (проведенными через 5 гПа) равно 1,5 см, радиус кривизны их 7 см.

5.8. Определить, на какой минимальной высоте от поверхности Земли скорость ветра для широты 55° совпадает по направлению со скоростью геострофического ветра зимой и летом, если коэффициент турбулентности, зимой равен 5 м²/с, летом 15 м²/с.

5.9. Оценить верхнюю границу пограничного слоя атмосферы на широте 55° в январе (коэффициент турбулентности равен 7 м²/с) и в июле (коэффициент турбулентности равен 21 м²/с).

5.10. Вывести формулы, описывающие распределение ветра в пограничном слое атмосферы при наличии термического ветра. При решении задачи принять k = соnst, 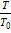= соnst, 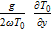= M = соnst, = N = соnst, где k – коэффициент турбулентности в пограничном слое, , – средние горизонтальные градиенты температуры, ω – вертикальная составляющая вектора угловой скорости суточного вращения Земли, T ₀ – температура атмосферы у поверхности Земли.

5.11. Построить спираль Экмана для широты φ = 55° при скорости геострофического ветра 10 м/с, и коэффициенте турбулентности 5 м²/с. Для каждой заданной высоты рассчитать: горизонтальные составляющие скорости ветра, угол наклона ветра, величину и направление силы Кориолиса (Н = 25 м, 100 м, 200 м, 1000 м). Плотность воздуха считать постоянной и равной 1,29 кг/м³.

5.12. Определить, на какой минимальной высоте от поверхности Земли скорость ветра для широты 60° равна половине скорости геострофического ветра, если коэффициент турбулентности равен 10 м ² /с. (Воспользоваться методом последовательных приближений).

5.13. Определить коэффициент турбулентности атмосферы на высоте 3 м над поверхностью Земли при отсутствии вертикального потока тепла, если известно, что на высоте h = 100 z ₀ (z ₀ – шероховатость подстилающей поверхности) скорость ветра равна 1 м/с.

5.14. Коэффициент турбулентности атмосферы на высоте 4 м равен 10 м²/с при отсутствии вертикального потока тепла, а скорость ветра на высоте 3 м - 2,5 м/с. Определить скорость ветра и коэффициент турбулентности на высоте 1 м?

5.15. Скорость ветра на высоте 2 м над уровнем над поверхностью Земли с шероховатостью 1 см равна 2,6 м/с. Считая, что стратификация атмосферы безразличная, найти коэффициент турбулентности на высоте 1 м.

5.16. Вычислить значения коэффициента турбулентности на высоте 0,25 м при турбулентных потоках тепла 300 Вт/м², если динамическая скорость равна 0,3 м/с, а шероховатость подстилающей поверхности равна 2 см. Принять ρ = 1,3 кг/м³ и Т ₀ = 273 K, С_P = 1005 Дж/(кг·K), В = 1.

5.17. Определить удельную влажность атмосферы на высоте 20 м от поверхности Земли при безразличной стратификации, если известны значения удельной влажности на меньших высотах.

z	1 м	2,7 м
s	5,4	5,2

5.18. Считая стратификацию атмосферы безразличной, определить скорость испарения по следующим данным о профиле абсолютной влажности:

z = 0,5 м	ρ_n = 7,3 г/м³
z = 1,0 м	ρ_n = 7,2 г/м³
z = 2,0 м	ρ_n = 7,2 г/м³
z = 4,0 м	ρ_n = 7,1 г/м³

если известно, что коэффициент турбулентности на высоте 1 м равен 0,085 м²/с.

5.19. Вычислить значения коэффициента турбулентности на высоте 0,5 м для масштаба Монина-Обухова L = 5 м (устойчивая стратификация) и L = –10 м (неустойчивая стратификация). Динамическая скорость равна 0,15 м/с, принять параметр В равным 1.

5.20. Определить температуру и удельную влажность на высотах 5 м и 10 м, если известно, что скорость ветра на этих высотах равна 2 м/с и 2,5 м/с соответственно, динамическая скорость равна 0,3 м/с, шероховатость подстилающей поверхности 3 см, турбулентный ноток тепла 0,2 Дж/(м²·с), скорость испарения 0,4 мм/ч. Принять плотность воздуха 1,3 кг/м³, температуру на уровне шероховатости 20°С, удельную влажность на этой поверхности 4,2 г/кг. Считать B = α_T = α_s = 1.

5.21. Определить частоту Вяйсяля-Брента, если известно, что температура равна 273 K, γ_e = 0,65 K/100м.

5.22. Определить период гравитационных колебаний, если известно, что температура равна 270 K, а вертикальный градиент температуры γ_e = 0,60 K/100 м.

5.23. Амплитуда гравитационных волн равна А = 90 м, определить фазовую скорость гравитационных волн в начальный момент, если γ_e = 0,60 K/100 м, Т = 265 K.

5.24. Найти фазовую и групповую скорость волн Россби длиной волны 500 км на широте 50° скорость западного переноса воздушных масс u = 50 км/ч.

5.25. Найти длину волны Россби, распространяющейся в атмосфере со скоростью 10° долготы в сутки на широте 45°, если скорость западного потока u = 30 км/ч.

5.26. Чему равна длина неподвижной волны Россби на широте 60°, если скорость зонального потока u = 50 км/ч?

5.27. Найти скорость распространения волн Россби длиной 25° на широте 45° в основном потоке, имеющем скорость 10 град/сутки.

5.28. Чему равна скорость распространения волн Россби, с периодом 6 суток на ширине 45° в потоке, имеющем скорость 20° долготы за сутки?

5.29. На какой широте скорость волн Россби, выраженная в градусах долготы за сутки, численно равна скорости, выраженной в м/с?

5.30. Найти скорость перемещения и период волн Россби длиной 30° долготы в потоке скоростью 15° долготы в сутки на широте 50°.

5.31. Какова длина стационарных волн Россби в потоке 5 град/сутки на широте 40°?

Приложение 1

НЕКОТОРЫЕ КОНСТАНТЫ

Универсальная газовая постоянная R^* = 8314 Дж/(кмоль·К)

Молекулярная масса сухого воздуха μ_с = 28,96 кг/кмоль

Газовая постоянная сухого воздуха R_с = 287,05 Дж/(кг·К)

Удельные теплоемкости сухого воздуха C_P = 1005 Дж/(кг·К)

C _V = 718 Дж/(кг·К)

Показатель адиабаты воздуха k = 1,4

Нормальное ускорение свободного падения g = 9,807 м/с²

Нормальное давление Р = 1013,25 гПа

Нормальная температура Т = 273,16 К; t = 0°С

Постоянная Стефана-Больцмана δ = 5,67·10^-8 Вт/(м²·К⁴)

Средний радиус Земли R_З = 6370 км

Плотность воздуха ρ =1,29 кг/м³ (при нормальных условиях)

Плотность воды ρ_w = 1·10³ кг/м³

Коэффициент молекулярной диффузии водяного пара D = 0,22 см²/с

Среднее расстояние от Земли до Солнца r _ʘ = 1,496·10¹¹ м

Диаметр Солнца d = 1,392·10⁹ м

Период суточного вращения Земли τ = 86400 с

Приложение 2

АТОМНЫЕ МАССЫ НЕКОТОРЫХ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ

Элемент	Символ	Атомная масса (а.е.м)
Водород	Н	1,008
Углерод	C	12,011
Азот	N	14,007
Кислород	O	15,999
Аргон	Ar	39,948

Приложение 3

УПРУГОСТЬ НАСЫЩЕННОГО ПАРА E НАД ВОДОЙ

t°C	гПа	t°C	гПа	t°C	гПа	t°C	гПа	t°C	гПа	t°C	гПа
-50	0,0635	-19	1,366	-8	3,348		7,754		15,96		31,67
-45	0,1111	-18	1,487	-7	3,617		8,128		17,04		42,43
-40	0,1891	-17	1,618	-6	3,906		8,718		18,17		56,23
-35	0,3138	-16	1,759	-5	4,214		9,345		19,36		73,77
-30	0,5082	-15	1,911	-4	4,544		10,01		20,63		95,85
-25	0,807	-14	2,075	-3	4,897		10,72		21,96		123,89
-24	0,883	-13	2,251	-2	5,274		11,47		23,37
-23	0,965	-12	2,440	-1	5,677		12,27		24,86
-22	1,054	-11	2,644		6,107		13,12		26,43
-21	1,150	-10	2,862		6,565		14,02		28,08
-20	1,254	-9	3,096		7,054		14,97		29,83

Приложение 4

УДЕЛЬНАЯ ТЕПЛОТА ИСПАРЕНИЯ ВОДЫ

t °C	–30	–15	–0	+0	+15	+30	+45
L, МДж/кг	2,939	2,837	2,835	2,500	2,465	2,430	2,394

Приложение 5-1

ВЯЗКОСТЬ, ТЕПЛОПРОВОДНОСТЬ И УДЕЛЬНАЯ ТЕПЛОЁМКОСТЬ ВОДЫ

t °C
10⁶ η, кг/(м·с)
10³ λ, Вт/(м·К)
C_P, кДж/(кг·К)	4,217	4,182	4,179	4,185	4,197	4,216

Приложение 5-2

ВЯЗКОСТЬ И ТЕПЛОПРОВОДНОСТЬ ВОЗДУХА

T, К
10⁶ η, кг/(м·с)	13,25	14,36	15,44	16,46	17,46	18,46	19,45
10³ λ, Вт/(м·К)	18,1	19,8	21,4	23,1	24,7	26,3	27,9

Приложение 6

C_f

10³

10²

0,1

0,1 1 10 10² 10³ 10⁴ R_e

⇐ Предыдущая 1 2 34

Воспользуйтесь поиском по сайту: