 |
Раздел 3. Термодинамические процессы в сухом и влажном воздухе.
|
|
|
|
Изменение температуры перемещающейся по вертикали массы сухого воздуха можно определить:
Если приток тепла 
, процесс можно считать адиабатическим.
Если температура частицы воздуха Тi отличается от температуры окружающих её масс воздуха Те, то на частицу действует сила плавучести (разность между силой тяжести и архимедовой подъёмной силой):
dF = (ρi - ρe) g dv.
При Ti > Те сила плавучести направлена вверх, при Тi < Те – вниз.
Атмосфера может находиться в устойчивом, безразличном или неустойчивом термодинамическом состоянии, в зависимости от того, в какую сторону действует сила плавучести на частицу воздуха при её вертикальном смещении из положения равновесия.
Критерием устойчивости является соотношение между вертикальными градиентами температуры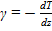 
для атмосферы в целом (γe) и для отдельной перемещающейся частицы (γi).
- условие устойчивости: γi > γe;
- условие неустойчивости: γi < γe;
- условие безразличного равновесия – (совпадение зависимостей Т(z) для атмосферы и частицы): γi = γe.
Поскольку процесс теплообмена протекает медленно, наиболее вероятно адиабатическое смещение частицы. В этом случае изменение температуры частицы характеризуется сухоадиабатическим градиентом:
γi = γa = 
.
Если при смещении частицы успевает произойти теплообмен, изменение температуры частицы характеризуется политропическим градиентом:
.
При политропическом процессе (удельная теплоёмкость c = const) термодинамические параметры состояния связаны соотношениями:
, 
,
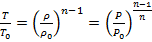где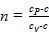 
– показатель политропы, 
– теплоёмкость воздуха.
Уровень конвекции zкв – высота, на которой поднимающая частица перегретого воздуха примет температуру окружающей среды:
|
|
|
(Тi, Te – температура частицы и среды на начальном уровне).
Энергия неустойчивости атмосферы в цилиндрической области диаметра d, располагающейся между уровнями давления P 1 и P 2 и имеющей температуру, в среднем на Δ T превышающую температуру окружающей среды:
.
Потенциальной температурой θ называется условная температура, которую приняла бы частица, сухого воздуха, если её адиабатически перевести на уровень, где давление составляет 1000 гПа. Главным свойством потенциальной температуры является её постоянство при адиабатических процессах. В частности, при турбулентных движениях отдельные массы воздуха "переносят" с собой свою потенциальную температуру. При смещении различных масс воздуха их потенциальные температуры выравниваются, и поэтому в идеально перемешанной области атмосферы θ не меняется по высоте.
.
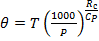Вертикальный градиент потенциальной температуры связан с вертикальным градиентом температуры соотношением:
.
При подъёме частицы насыщенного влажного воздуха без теплообмена с окружающей средой изменение температуры частицы с высотой характеризуется влажноадиабатическим градиентом γa':
ЗАДАЧИ
3.1. Вычислить и сравнить сухоадиабатические градиенты температуры для атмосферы Земли и Марса. Считать атмосферу Марса состоящей из углекислого газа. Масса Марса составляет 0,11 от массы Земли, средний радиус – 0,53 от радиуса Земли.
3.2. Результаты измерения температуры атмосферы у земной поверхности (t 0°C) и на высоте 1 км (t 1°C):
а) t 0°C = 20°C; t 1°C= 9°C;
б) t 0°C = 12°C; t 1°C= 4°C;
в) t 0°C = 18°C; t 1°C= 7°C;
г) t 0°C = 15°C; t 1°C= 8°C;
д) t 0°C = 2°C; t 1°C= 14°C;
Считая изменения температуры по высоте линейным, определить устойчивость атмосферы по отношению к адиабатическому перемещению сухого воздуха.
3.3. Температура атмосферы (t °C) изменяется по высоте (z, км) по закону:
а) t = 15 – 6 z – 2 z 2;
|
|
|
б) t = 30 – 12 z + z 2;
в) t = z – 2 z 2;
г) t = 20e-0,8 z;
Определить области устойчивой и неустойчивой стратификации для сухого воздуха. Возможно ли в какой-либо точке атмосферы статически безразличное состояние?
3.4. Состояние поднимающихся частиц сухого воздуха изменяется по политропе с показателем n = 1,6. В окружающей атмосфере температура падает на 11°С при подъёме на каждый километр. Определить состояние устойчивости атмосферы.
3.5. Состояние атмосферы статически безразлично по отношению к адиабатическим смещениям частиц. Определить вертикальную устойчивость атмосферы по отношению к смещениям частиц с теплообменом для следующих случаев:
а) подъём с подводом тепла;
б) подъём с отводом тепла;
в) спуск с отводом тепла;
г) спуск с подводом тепла.
3.6. Температура атмосферы уменьшается по высоте с градиентом 13 K/км. В поднимающейся массе сухого воздуха каждый её грамм отдает в окружающую среду за счёт теплопроводности 2 мДж при подъёме на 1 м. Определить, с каким вертикальным градиентом меняется температура поднимающейся частицы. Будет ли состояние атмосферы устойчивым?
3.7. Изменение температуры атмосферы по высоте описывается уравнением: t = 20°C – 5 
.
Какое количество тепла на единицу массы должна получать или отдавать частица сухого воздуха при подъёме на каждый километр, чтобы соотношение равновесия было безразличным?
3.8. Перегретая на 5°С частица сухого воздуха адиабатически поднялась от земной поверхности на высоту 2500 м, где её движение прекратилось. Определить градиент температуры в атмосфере.
3.9. Температура атмосферы падает на 8°С при подъёме на каждый километр. Частица сухого воздуха у земли перегрета на 10°С по сравнению с окружающей средой. Определить, до какого уровня поднимется, эта частица, если её подъём будет протекать в следующих условиях:
а) адиабатически;
б) по политропе с показателем n, отличающимся на 0,1 от показателя адиабаты за счёт теплообмена частицы с окружающей средой.
3.10. Определить энергию неустойчивости, сосредоточенную в облаке диаметром 6 км, нижняя граница которой расположена на уровне 800 гПа, а верхняя – на уровне 200 гПа, при средней разности температур в облаке и окружающей атмосфере 5°С. Сравнить полученную энергию с энергией средней атомной бомбы (108 МДж).
|
|
|
3.11. Вывести формулу, связывающую потенциальную температуру с термодинамической температурой T и давлением Р. Вычислить потенциальную температуру в той точке траектории шара-зонда, где находящиеся на нём датчики давления и температуры показывали соответственно 700 гПа и 5°С. Считая атмосферу идеально перемешанной, определить термодинамическую температуру на уровне 850 гПа.
3.12. Температура на изобарической поверхности 800 гПа равна 8,6°С. Вычислить потенциальную температуру на этой высоте.
3.13. Вывести формулу 
.
3.14. Изменение давления и температуры атмосферы по высоте дано таблицей:
| z, м | ||||
| P, гПа | ||||
| t, °C | 8,0 | 6,5 | 5,0 | 3,5 |
Для каждого уровня определить состояние устойчивости атмосферы по отношению к влажноадиабатическому подъёму частицы насыщенного воздуха.
3.15. Известно распределение температуры в атмосфере: t = 10°C – 4 . У земной поверхности давление воздуха 1000 гПа, точка росы 10°С. Определить состояние устойчивости атмосферы в приземном слое.
3.16. Вычислить влажноадиабатический градиент температуры по следующим данным: начальное давление P 0 = 1000 гПа, P 0 = 500 гПа; начальная температура
t 0 = 17°С, t 0 = 7°С, t 0 = –3°С.
Раздел 4. Физические процессы образования облаков и осадков.
При наблюдающихся в атмосфере температурах водяной пар может изменять своё агрегатное состояние, переходя в жидкое (вода) и твердое (лёд) состояния. В результате конденсации и сублимаций водяного пара в атмосфере возникают облака и туманы. В свободной атмосфере важнейшим процессом, приводящим к облакообразованию, является вынужденный подъём воздушных масс. При восходящем движении понижается температура воздуха, что вызывает пересыщение водяного пара и конденсационный рост капель. Уровень конденсации zконд., на котором воздух достигает состояния насыщения f = 100%, совпадает с нижней границей облака. Зная относительную влажность f 0 и температуру воздуха T 0 у поверхности Земли, нижнюю границу облаков можно определить по формуле:
|
|
|
,
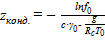С = 0,073 
при Т = 273 K и С = 0,067 при Т = 283 K.
Для расчётов можно использовать приближенную формулу:
[км]
Капли меняют свои размеры посредством молекулярного обмена. Скорость роста капли вследствие конденсации можно рассчитать по формуле:
,
где rк – радиус капли в данный момент времени; 
– радиус капли в начальный момент, t – время роста капли; D – коэффициент молекулярной диффузии водяного пара в воздухе; ρ – плотность воздуха; ρw – плотность воды; s – удельная влажность воздуха,
,
где Е (Т) – упругость насыщения водяного пара над каплей, для расчётов её можно принять равной упругости насыщения над плоской поверхностью чистой воды (приложение 3). После того как капли достигают размеров rк = (2–6)·10-5 м, преобладающую роль играют процессы коагуляции облачных элементов. Коагуляция обусловлена различной скоростью падения облачных элементов, турбулентным и броуновским движением, электростатическими силами и т.д. Капли разных размеров движутся с различной скоростью. При малых числах Рейнольдса
,
где η - динамический коэффициент молекулярной вязкости воздуха (приложение 5), считая каплю шарообразной, силу сопротивления движению капли можно оценить по закону Стокса:
Тогда скорость установившегося движения капель пропорциональна квадрату радиуса капли
Формула справедлива для капель размером rк = 10-7 –5·10-5 м. Для расчёта силы сопротивления более крупных капель (Re > 1) можно воспользоваться формулой
где cf – коэффициент сопротивления, зависящий от числа Рейнольдса Re (приложение 6). Скорость установившегося движения капель rк > 5·10-5 и определяется соотношением:
При rк = 10-2 м капли распадаются.
Важнейшей характеристикой облаков и туманов является их водность. Абсолютной водностью δ называют массу капель, воды и кристаллов льда, содержащихся в единичном объёме воздуха (чаще всего в 1 м3).
ЗАДАЧИ
4.1. Определить высоту уровня конденсации, если температура у поверхности Земли 10,0°C, относительная влажность 55%. Построить график адиабатического подъёма единичной массы воздуха, определить её температуру на уровне конденсации. Вертикальный градиент температуры принять равным 14 K/км.
4.2. Рассчитать высоту нижней границы облачности, воспользовавшись приближенной формулой при значениях относительной влажности у поверхности Земли 80%, 50%, 30%. Какова эта высота, если относительная влажность у Земли равна 100%?
4.3. Определить относительную влажность воздуха у поверхности Земли, если уровень конденсации наблюдается на высоте 1 км, температура у поверхности Земли равна 10,0°С, наблюдается вынужденный подъём воздушных масс.
|
|
|
4.4. Определить изменение размеров капли за счёт конденсации за t = 1, 5, 10 с, если температура воздуха 20°C, давление 1000 гПа, удельная влажность воздуха 15,6·10-3. Для расчётов воспользуйтесь приложением.
4.5. Определить радиус капли, если наблюдался конденсационный рост её в течение 20 с, начальный радиус капли 5·10-6 м, давление 1000 гПа, удельная влажность 10,3·10-3, температура воздуха 0,0°С.
4.6. Капли могут изменять свои размеры за счёт процесса испарения. Определить время существования капель, если начальный радиус капель 
= 1·10-6 м; 3·10-6 м; 1·10-5 м; 5·10-5 м. Удельная влажность воздуха 5·10-3, температура воздуха 10,0°С, давление 1000 гПа. Для расчётов воспользуйтесь приложением.
4.7. Время падения капли из облака превышает 1 мин. Достигнут ли осадки земной поверхности, если радиус капель rк = 25·10-5 м и более, удельная влажность воздуха s = 0,6·10-3, температура воздуха 15,0°С, давление 1000 гПа. Для расчётов воспользуйтесь приложением.
4.8. Какие силы действуют на каплю, находящуюся во взвешенном состоянии? Определить скорость установившегося движения капель, радиус которых rк = 10-7 м, 10-6 м, 10-5 м. Температура воздуха 7,0°С.
4.9. Вычислить скорость установившегося движения капли радиусом 1 мм. Для определения коэффициента сопротивления воспользуйтесь графиком (приложение 6). Задачу решать методом последовательных приближений, задав на первом приближении Cf = 0,5.
4.10. Доказать, что скорость роста капли за счёт, гравитационной коагуляции определяется выражением 
. Вычислить скорость роста капли, если водность облака δ = 0,4·10-3 кг/м3, скорость установившегося движения капли vs = 0,6 м/с.
4.11. Чему равна водность облака, если скорость роста капли за счёт гравитационной коагуляции составляет 10-7 м/с. Скорость установившегося движения капли vs = 0,6 м/с.
4.12. Определить скорость восходящего потока, если за счёт процесса ламинарной коагуляции капли, радиус которых первоначально составлял 2·10-7 м, возросли до размеров rк = 5·10-5 м.
4.13. Чему равна скорость восходящего потока, если в результате процесса турбулентной коагуляции размер капель 
= 2·10-4 м увеличился до критического rк = 1·10-2 м.
4.14. Вычислить скорость восходящего потока, если в результате процесса коагуляции размеры капли изменились от = 6·10-7 м до rк = 1·10-2 м. В турбулентной области принять cf = 5.
|
|
|
