Необходимость использования качественных фиктивных переменных в регрессионном анализе.

В больш-ве случаев независимые переменные в регресс. моделях имеют непрерывные области изменения. Однако теория не накладывает никаких ограничений на характер коэф-тов регрессии, некот. переменные могут принимать всего два значения или в более общей ситуации – множество дискретных значений.

Необх-сть рассмотрения таких переменных возникает в случаях, когда надо оценить какой либо качественный признак, т. е. Когда факторы, вводимые в ур-ие регрессии являются качест-ми и не измеряются по числовой шкале. Н-р, при исследовании зависимости з/п от различных факторов может возникнуть вопрос, влияет ли на ее размер наличие у работника высшего образования; существует ли дискриминация в оплате труда женщин и мужчин. Одним из решений данного примера явл. оценка отдельных регрессий для каждой категории, а затем изучение различий м/у ними. Другой подход состоит в оценке единой регрессии с использованием всей совокупности наблюдений и измерений степени влияния качественного фактора посредством введения фиктивной переменной. Она является равноправной переменной наряду с др-ми переменными моделями. Ее фиктивность закл. лишь в том, что она количеств-м образом описывает качественный признак. Второй подход обладает след. преимущ: 1) это простой способ проверки, явл. ли воздействие качественного признака значимым; 2) при условии выполнения опред. предположений регрессионной оценки оказывается более эффективным.

 

33.Способы введения фиктивных переменных в регрессионную модель. Фиктивные переменные вводятся в модель регрессии след. образом. Н-р,

1) пусть Х=(х1, х2, …, хК) – это набор объясняющих независимых переменных,

Y(x)= f(x) –это ф-ия, описывающая зависимость з/п от различных факторов.

Тогда первоначальная модель будет выглядеть след. образом: Y(x)= a1*x1+a2*x2+…+aK*xK+∑ (5.1).

Надо определить влияние такого фактора, как наличие или отсутствие высшего образования. Для этого вводится фиктивная переменная d. Если работник имеет высшее образование, то d=1, если нет, то d=0. При введении фиктивной переменной ур-ие регрессии принимает след. вид Y(x)= a1*x1+a2*x2+…+aK*xK+ σ d+∑=x’*a+ σ d+∑ (5.2), где σ – коэф-т регрессии при фиктивной переменной.

При изучении модели (5.2) считают, что средняя з/п есть x’*a – при отсутствии высшего образования, x’*a+ σ – при его наличии. Т. о., σ интерпретируется как среднее изменение з/п при переходе из одной категории в др-ю.

<График>

К полученному ур-ию нужно применить МНК и получить оценки соответствующих коэф-тов. Станд. ошибки коэф-тов при фиктивных переменных используются для проверки гипотез и построения доверительных интервалов. Наиболее распр. их применение состоит в проверке значимости отличия коэф-тов от 0. Она выполняется делением коэф-та на станд. ошибку для получения t-критерия Стъюдента. Расчетные значения сравниваются с критическим табличным значением при заданном уровне значимости. Качественные переменные могут отвечать не только за сдвиги у постоянного члена, но и за наклон линии регрессии. В данном случае используется фиктивная переменная для коэф-та наклона, к-ая наз-ся переменная взаимодействия.

В примере 1 был рассмотрен случай зависимости з/п от наличия высшего образования без учета опыта работы по данной специальности.

Для рассмотрения влияния этого фактора вводится новая фиктивная переменная zdx,

тогда Y(x) = x’*a+ σ d+ zdx +∑; Y(x) = σ d+ x*(a+zd) +∑; (5.3).

Если d=0, то коэф-т при Х как и раньше равен а, если d=1, то коэф-т приобретает вид (a+z).

Поэтому величина z рассматривается как разность между коэф-том при показателе наличия высшего образования для работника, к-ый имеет опыт работы, и коэф-том при показателе наличия высшего образования для работника без опыта работы. Качественные различия можно формализовать с помощью любой переменной, принимающей два значения. Однако в эк-ой практике обычно используется система 01, поскольку в этом случае интерпретация выглядит наиболее просто.

 

34.Проверка регрессионной однородности выборочной совокупности (критерий Чоу). Сравнение двух регрессий. Ранее предполагалось, что изменение значения качеств-го фактора влияет лишь на изменение свободного члена. Но это, не всегда так. Следов-но, необходимо представить, что изменение качеств. фактора может привести как к изменению свободного члена уравнения, так и наклона прямой регрессии. Обычно это характерно для временных рядов экон-их данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. Для сравн. двух регрессий м/б использован тест Чоу. Суть теста в следующем: пусть выборка имеет объем n. Через 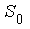обозначим сумму квадратов отклонений значений от общего уравнения регрессии. Пусть есть основание предполагать, что целесообразно общую выборку разбить на две подвыборки объемами и соотв. 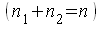и построить для каждой из выборок уравнение регрессии. Через и 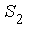обозначим суммы квадратов отклонений значений каждой из подвыборок от соотв. уравнений регрессии. Очевидно, что возможно лишь при совпадении коэф. регрессии для всех трех уравнений. Чем сильнее различие в поведении Y для двух подвыборок, тем больше значение 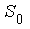будет превосходить . Тогда разность может быть интерпретирована как улучшение качества модели при разбиении интервала наблюдений на два подынтервала. Следовательно, дробь определяет оценку уменьшения дисперсии регрессии за счет построения двух уравнений вместо одного. При этом число степеней свободы сократиться на , т. к. вместо параметра объединенного уравнения теперь необходимо оценивать параметра двух регрессий. Дробь , необъясненная дисперсия зависимой переменной при использовании двух регрессий. Тогда напрашивается вывод о том, что общую выборку целесообразно разбить на два подынтервала только в случае, если уменьшение дисперсии будет значимо больше оставшейся необъясненной дисперсии. Данный анализ осуществляется по стандартной процедуре сравнения дисперсий на основе F -статистики. Использование указанной F -статистики (теста Чоу) осуществляется достаточно просто. Однако оно менее информативно, нежели общий анализ сложной регрессии с фиктивными переменными, осуществляемый на базе t -статистик (с учетом вклада каждой фиктивной переменной), коэффициента детерминации и статистики Дарбина-Уотсона. Однако тест Чоу вполне достаточен, если требуется установить, что зависимости в подвыборках различаются.

 

 

35.Регрессионные модели с колич-ми и качественными переменными (ANCOVA-модели). Регр. модели, содерж. лишь качеств. переменные, наз. ANOVA-моделями (моделями дисперсион-го анализа). Однако такие модели в экономике крайне редки. Гораздо чаще встреч-ся Модели, в кот.объясняющие переменные носят как колич-ый, так и качест-ый хар-р, и наз-ся ANCOVA-моделями (моделями ковариационного анализа). ANCOVA-модель при наличии у фиктивной переменной двух альтернатив. Вначале рассмотрим простейшую ANCOVA-модель з/п сотрудника фирмы (Y) с одной колич. и одной качеств., имеющей два альтернативных состояния где X — стаж сотрудника; D — пол сотрудника. Т. е. 0 — если сотр — женщина и 1, если сотрудник — мужчина. Тогда ожидаемое значение з/п сотр-в при x годах труд. стажа будет иметь вид З/п в данном случае явл. линейной функцией от стажа работы. И для мужчин и для женщин з/п меняется с одним и тем же коэф. пропорц-сти . А вот своб. члены в моделях отличаются на величину . Проверив с помощью t -критерия статистические значимости коэф-тов и , можно опред-ть, имеет ли место в фирме дискриминация по половому признаку. Если эти коэф. окажутся статистически значимыми, дискрим-я есть. Более того, при она будет в пользу мужчин, при — женщин. В данном случае пол сотрудников имеет два альтернат. значения, и в модели это отражается одной фиктивной переменной. Коэффициент в модели иногда называется дифференциальным коэф. свободного члена, т/к он показывает, какой величиной отличается свободный член модели при значении фиктивной переменной, равной единице, от свободного члена модели при базовом значении фиктивной переменной.

36.Использование фиктивных переменных в анализе сезонности. Многие экономические показатели напрямую связаны с сезонными колебаниями. Например, спрос на туристические путевки, охлажденную воду и мороженое существенно выше летом, чем зимой. Спрос на обогреватели, шубы выше зимой. Некоторые показатели имеют существенные квартальные колебания и т. д. Обычно сезонные колебания характерны для временных рядов. Устранение или нейтрализация сезонного фактора в таких моделях позволяет сконцентрироваться на других важных количественных и качественных характеристиках модели, в частности на общем направлении развития модели, так называемом тренде. Такое устранение сезонного фактора называется сезонной корректировкой. Существует несколько методов сезонной корректировки, одним из которых является метод фиктивных переменных. Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, так как в этом случае вполне вероятны ошибки спецификации. Вначале рассматривается математическая модель. Определяется статистическая значимость коэффициентов. Если в этой модели дифференциальные свободные члены оказываются статистически незначимыми, то делают вывод, что квартальные (сезонные) изменения несущественны для рассматриваемой зависимости [12].

В анализе временных рядов принято рассматривать следующие формы взаимосвязи: аддитивная и Мультипликативная модель изучения сезонности.

 

 

37.Модели с завис-ми качеств (альтерн-ми) переменными. Логит- и пробит-модели,оценив-ние их параметров. Представим модели результата сдачи с первой попытки экзамена в ГАИ в виде примера 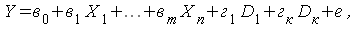где — кол-во часов вождения; — средний %% выпуск, сдающих экзамен с первой попытки; — исп. компьют. методики обучения. В этой ситуации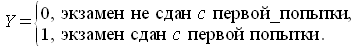

Пусть 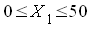ч, Тогда получим сл. модель: Модели данного вида называется линейными вероятностными моделями (linear probability models ) (LPM-моделями). LPM имеет определенные ограничения: 1. Случ. отклонения в данных моделях не явл. нормальными случ-ми величинами, а, имеют биноминальное распределение. 2. Случайные отклонения не обладают свойством постоянства дисперсии (гомоскедастичности). 3. Применение модели LPM весьма проблематично с содержательной точки зрения. Для преодол. недостатков LPM-моделей необх. исп. такие модели, в кот. 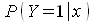не будут,нарушаться неравенства , и зависимость между и х не будет иметь линейный характер, а будет удовлетворять закону убывающей эффективности. В кач-ве одного из вариантов преодоления недостатков модели LPM можно предложить logit модель. Пример:

Вы изучаете поведение покупателей в Вашем магазине и хотите изучить чем поведение купивших отличается от поведения людей, не сделавших покупку. В этом случае факт покупки - зависимая бинарная величина, а поведение человека в магазине и половозрастные характеристики посетителя - факторы. Введем следующие обозначения: Покупка - значение "1", клиент ушел без покупки - "0".

T - время проведенное в магазине;Y - возраст клиента;

K - внешняя респектаб-ность клиента по 5-бальной шкале; е(i) - "ошибки". В e(i) -попадают отклонения, которые не объяснены моделью. В итоге, модель имеет следующий вид: Покупка(i) = a*T(i)+b*Y(i)+c*K(i)+e(i)

По ряду причин, применение линейного оценивания здесь дает некорректные результаты, поэтому для оценки коэффициентов"а,b,c" задается условное распределение положительного решения о покупке в зависимости от дохода. В случае если рассматривается стандартное нормальное распределение, модель называется probit, если логистическое, то - logit.

 

38.Системы уравнений, используемых в эконометрике. Независимые системы. Рекурсивные системы. Сист. ур-й в эконометрич. исслед. может быть построена по-разному. система независимых уравнений, когда каждая зависимая переменная рассматривается как функция одного и того же набора факторов :

Набор факторов в каждом ур-нии может варьировать. Каждое ур-ние сист. независ. ур-ний может рассматр-ся самостоятельно. Для нахожд. его параметров исп. метод наименьших квадратов. Т.е, каждое ур-ние этой сист. явл. ур-ем регрессии. Т.к. фактич. знач. завис. переменной отлич. от теорет.на величину случ. ошибки, то в каждом ур-нии присутствует величина случайной ошибки . Если завис. переменная одного ур-ния выступает в виде фактора в другом ур-нии, то исследователь может строить модель в виде системы рекурсивных уравнений

Завис. переменная включает в каждое послед. ур-ние в кач-ве факторов все завис. переменные предшествующих ур-ний наряду с набором факторов . Каждое ур-ние может рассмат. самост-но, и его параметры определяются методом наименьших квадратов.

 

39.Системы одновременных (совместных) уравнений. Структурная и приведенная формы модели. Наиб. распростр. в эконометрич. исслед. с ист. взаимозависимых ур-ний. В ней одни и те же завис. переменные в одних ур-ях входят в левую часть, а в др — в правую часть сист:

Каждое ур-ние системы одновр. ур-ний не может рассмат. самостоят. С этой целью исп. спец. приемы оценивания. Эндогенные переменные — завис. переменные, число кот.равно числу ур-ний в системе; обозначаются через . Экзогенные переменные — предопределенные переем., влияющ. на эндог-ые переем., но не завис. от них. Обоз. . Классиф. переменных на энд. и экз. зависит от теорет. концепции принятой модели. Экономич. переменные могут выступать в одних моделях как энд., а в других как экз. переменные. Внеэкономич. переменные (климат. условия, соц. положение, пол, возрастная категория) входят в систему только как экз. переменные. В кач-ве экз. переменных могут рассм. значения энд. переменных за предшествующий период времени (лаговые переменные). Структурная форма модели позв. увидеть влияние изменений любой экз. переменной на значения энд. переменной. Целесообразно в качестве экз.переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения энд. переменных.

Стр. форма модели в правой части содержит при энд. переменных коэффициенты и экз. переменных — коэффициенты , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т. е. под подразумевается , а под — соответственно . Поэтому свободный член уравнении системы отсутствует. Обычно для определения стр. коэффициентов модели стр. форма модели преобразуется в приведенную форму модели. Для структурной модели вида

Прив. форма модели имеет вид

Из стр.модели можно выразить следующим образом

Подставляя во второе ур-ние , имеем

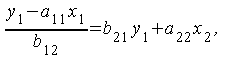откуда

Преобразуя аналогично второе уравнение получим

т. е. система принимает вид

 

 

40.Проблема идентифицируемости модели. При переходе от приведенной формы модели к структурной сталкив. с проблемой идентификации, кот. явл. единственностью соответствия м/у привед. и структурной формами модели.

Структурная модель (6.3) в полном виде содержит параметров, а приведенная форма модели — параметров, Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно параметров структурной модели не могут быть однозначно определены из параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Уменьшение числа структурных коэффициентов модели возможно и другим путем: например, путем приравнивания некоторых коэффициентов друг к другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. На структурные коэффициенты могут накладываться, например, ограничения вида .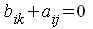

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

 

 

41.Необходимое и достаточное условия идентиф-мости модели. Структурн.модель пред-ет систему совместных ур-ний, кажд. из кот.треб-тся проверять на идентификацию. Модель счит.идентифицируемой, если каждое ур-ние системы идентифицируемо. Чтобы ур-ние было идент-мо, необх., чтобы число предопредел-х переменных, отсутств-их в данном ур-нии, но присутств-их в системе, было равно числу эндогенных переменных в данном ур-нии без одного. Если обозн. число эндогенных переменных в i -м ур-нии H, а число экзогенных (предопред) переменных, кот содержатся в системе, но не входят в данное ур-ние, — D, то условие идентифицируемости модели в виде след. счетного правила:

Обозначение переменных	Условие идентификации
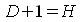
	уравнение идентифицируемо
	уравнение неидентифицируемо
	уравнение сверхидентифицируемо

Ур-ние идентиф-емо, если по отсутств. в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: