Характерные типы системы массового обслуживания (СМО), показатели функционирования СМО.

По числу каналов обслуживания - на одноканальные (с одним обс. устройством) и многоканальные (с большим числом обс. устройств).

В завис. от условий ожидания требованием начала обслуж. - СМО с отказами (потерями) и с ожиданием. В СМО с отказами требования, пост. в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются. В СМО с ожиданием треб., заставшее все обслуживающие каналы занятыми, ставится на очередь до освобожд. любого из обслуживающих каналов.

Системы с огранич. ожиданием и с неогранич. ожиданием. В системах с огр. ожид. может ограничиваться либо длина очереди, либо время пребывания в очереди.

По месту нахожд. источника требований - разомкнутые (источник треб. вне системы) и замкнутые (источник в самой системе).

Среднее число треб., поступ. в с/о за ед. времени, назыв. интенсивностью поступления требований: где Т — ср. значение интервала м/у поступл. очередных требований. При простейшем потоке треб., их распределение, подчиняются закону распределения Пуассона: вероятность того, что в обс. систему за время t поступит именно k требований где — ср. число треб., пост. на обс. в ед. в.

Время обсл. одного требования () — случ. величина, кот. может изменяться в большом диапазоне. Она зависит от стабильности работы самих обсл. устройств, так и от разл. параметров, пост. в систему, требований (к примеру, разл. грузоподъемности трансп. ср-в).

Показательный закон распределения времени обс. имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Напр, когда основная масса треб. обслуживается быстро, а продолжит.- встречается редко.

Вероятность события, что время обсужив. продлиться не более чем t, равна где v — интенсивность обс. одного треб. одним обслуж. устройством, кот. определ. из соотношения , где — среднее время обсл. одного требования одним обслуживающим устройством.

При наличии нескольких обсл. устройств одинаковой мощности закон распред. времени обсл. несколькими устройствами будет также показательным где n — количество обслуживающих устройств.

Важным параметром СМО явл. коэффициент загрузки , кот. опред. как отношение интенсивности поступления требований к интенсивности обслуживания v где a — коэф загрузки; — интенсивность поступления треб систему; v — интенсивность обсл. одного треб одним обсл устройством. Следов, получаем, выражение

55.Модели массового обслуживания с отказами, их параметры. При этом СМО состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью , зависящей, в общем случае, от времени Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуж. заявки продолжается в течение случ. времени , распределенного по показат-му закону с параметром : . Из этого следует, что «поток обслуживания» — простейший, с интенсивностью . Требуется найти:

• абсолютную пропускную способность СМО (А);
• относительную пропускную способность СМО (q).

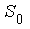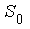Рассмотрим единств. канал обслуживания как систему S, кот. может находиться в одном из двух состояний: — свободен, — занят. Из состояния в систему, очевидно, переводит поток заявок с интенсивностью ; из в 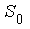— «поток обслуживания» с интенсивностью . Вероятности состояний: и Очевидно, для любого момента t:

Составим дифференциальные уравнения Колмогорова для вероятностей состояний согл. правилу, данному выше:

Для одноканальной СМО с отказами вероятность есть не что иное, как относительная пропускная способность q. Действительно, есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно

.

В пределе, при , когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно

.

Зная относительную пропускную способность q, легко найти абсолютную А. Они связаны очевидным соотношением

Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа

или среднюю часть не обслуженных заявок среди поданных [15]:

.