Метод регрессивного анализа .

Прогнозируемое значение материальных потока рассчитывается как значение математической функции,наиболее точно описывающей изменение значений материальных потока за несколько предыдущих периодов.

При этом способе прогнозирования используется метод наименьших квадратов, исходные положения которого приведены ниже:

Пусть имеется таблица данных:

 

 

Таблица.2.1

i				…	n
				…
				….

 

По характеру расположения точек () установлено,что они располагаются условно на прямой y=ax+b (рис.2.1)

Рис(2.1)

 

Сущность метода наименьших квадратов состоит в том, что искомую прямую y=ax+b выбирают таким образом, чтобы сумма квадратов отклонений y_i –y была бы наименьшей.

Таким образом,неизвестные параметры а и b находятся из условия, что сумма

или имела наименьшие значение. Поскольку , – постоянные числа, то указанная сумма есть функция двух параметров a и b:

S(a,b) = (2.5)

Чтобы найти значения параметров а и b, воспользуемся необходимым условием экстремума функций двух переменных: найдем частные производные от S (a, b) по а и b и приравняем их к нулю

(2.6)

или

(2.7)

или

(2.8)

Значения а и b найдем, решив систему методом определителей:

 

(2.9)

 

(2.10)

 

 

Таким образом,для определения а и b получили систему уравнений первой степени.Доказано,что система 2 имеет единственное решение, и что при найденных а и b функция S (a,b) имеет минимум.(Проверяются достаточные условия существования экстремума функции двух вариантов).

Подставляя найденные значения а и b в уравнение y=ax+b, получим линейную функцию, наилучшим образом отражающую зависимость между величинами x и y.

Теперь приведем пример определения прогнозируемого материального потока каждый из вышеперечисленных методов.В таблице 2.2 заданы размеры материальных потоков в соответствующие временные периоды.

Таблица 2.2

Изменение материального потока по годам

Годы,
Мат.поток N, тыс.т/год	41,3	41,9	47,8	52,5	56,7

 

1.Определение методом наивного прогноза.

В этом случае прогноза на год составит:

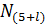=56,7 (тыс.т/год)

 

2.Расчет методом простого среднего.

Для исходных данных,приведенных в таблице 2.1, получим:

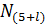= =48,04 (тыс.т/год)

 

3.Определение методом скользящего среднего.

Предложим, что эксперты присвоили следующие оценки весов:

; ; .

 

Расчет значения прогноза выполнен по формуле (2.3) при ограничении (2.4):

 

51,66 (тыс.т/год)

 

4.Определение методом регрессивного анализа.

В общем виде уравнение искомой функции может быть записано следующим образом:

(2.11)

 

где - значение функции в t-й год;

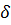- погрешность, показывающая величину отклонения

теоретических значений от экспериментальных.

Функция может иметь любой вид: прямая, парабола и т.д. Выбор функции, наиболее точно описывающей заданные изменения материального потока, осуществляется на основании минимизации значения погрешности 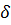, которое рассчитывается по формуле:

 

(2.12)

 

где – значение материального потока в t-й год (фактическое);

n – число наблюдений;

p – число параметров в уравнении тренда (число неизвестных).

Для анализа принимаем две функции: линейную и полином 2-го порядка:

		(2.13)
		(2.14)

 

где – начальный уровень тренда;

– средний абсолютный прирост в единицу времени, константа линейного тренда;

– квадратичный параметр равный половине ускорения, константа параболического тренда.

Значения коэффициентов a,b,с определены с помощью метода

наименьших квадратов.

Продифференцируем каждое уравнение и составим систему нормалоьных уравнений:

ü для линейного тренда:

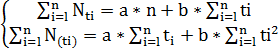(2.15)

 

ü для параболического тренда:

 

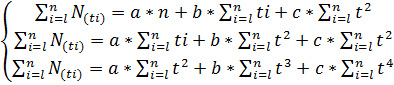(2.16)

 

 

Для упрощения расчетов используем метод отсчета времени от условного начала.Обозначим в ряду изменения значений времени (t) таким образом, чтобы , стала равна нулю.

Представим метод расчета и его результаты в виде таблицы: (2.3)

 

 

Таблица 2.3

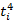
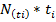
№								f
	-2	41.3		-6		-82.6	165.2	39.72	2.5	40.58	0.51
	-1	41.9		-1		-41.9	41.9	43.86	3.84	43.46	2.43
		47.8							0.04	47.6	0.04
		52.5				52.5	52.5	52.14	0.12	51.14	0.57
		56.7				113.4	226.8	56.28	0.17	57.14	0.22
Σ						41.4	486.4		6.67	240.5	3.77

Расчет параметров тренда

 

ü для линейного тренда:

(2.17)

 

ü для параболического тренда:

(2.18)

Отсюда:

Для линейного тренда:

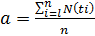(2.19)

 

b= (2.20)

Получаем:

а =

b=

 

Для линейного тренда

Для параболического тренда

Так как 1,83 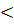1,94, линейный тренд является более предпочтительной функцией, т.е. В этом случае прогноз искомого параметра целесообразно определять по формуле линейного тренда,т.е.

 

(тыс.т/год)

Графики и приведены на рисунке 2.2

 

Рис.2.2 Графики функций и .

 

Итак, планируемый размер материального потока в 2010 году, определенный методом регрессионного анализа составляет 6046 тонн.

Вывод: в данном разделе определил прогнозирование материальных потоков, планируемый размер материального потока в 2010 году, определенный методом регрессионного анализа составляет 6046 тонн.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: